| A | B | C | D | E | ||
| 問題文 | ■ | ■ | ■ | ■ | ■ | |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | AC |
全体感想
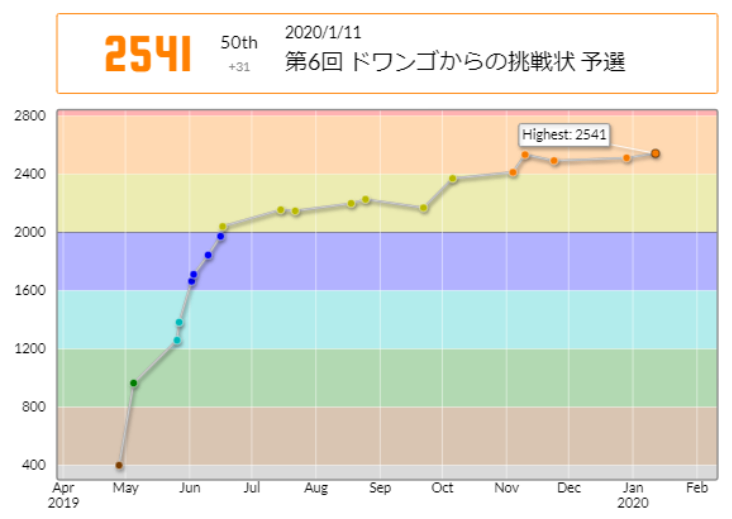
107分4完10ペナで、50位でした。
問題Dで、ロジックが誤っていて、原因の特定・修正に時間を使いました。提出は、計画的なWA提出でしたが、もう少し回数を減らせましたね。
問題Dが着手 2 問目だったため、ここで事故って、焦って精神的に追いつめられると、最終得点 200 点もありうる展開です。
1時間使ってしまったものの、とにかく落ち着いて、ロジックを確認しなおして、ACを得ました。コードもあとからいじいじしたので、ひどい有り様になっています。
もう1, 2バグ踏んでもおかしくなかったですが、耐え切りました。
数か月前なら、さらにバグらせてたり、泣きそうな精神状態のまま他の問題を右往左往して破滅したりしている可能性がもっと高かったかもしれません。こういうところで、実力向上が利いてきていると前向きにとらえていきます。
問題B – Fusing Slimes
各地点を、スライムは1度だけ出発します。その瞬間の移動先の確率分布を考えます。
この際、自分の左側に居るスライムの状況は関係ありません。よって、$n$ 匹のスライムが居て、自分が左端のスライムであるときに考察を進めればよさそうです。
移動する区間 $[x_i, x_{i+1}]$ の個数を「距離」と呼んでいきます。
・距離 1 以上すすむ確率:1
・距離 2 以上すすむ確率:1/2
・距離 3 以上すすむ確率:1/3(スライム 1,2,3 の中で最後だったらよいので)
はじめ数分間、「スライム 2 よりも後で($1/2$)さらにスライム 3 よりも後で ($1/2$)、あわせて確率 $1/4$」などと考えてしまいそうに。
これ、過去問でも何度かやってしまった思考(毎回すぐ気づくのですが。$3! = 6$ は $4$ で割れないですし)。(「1番が2番より後」という情報が入ると、「1番が3番より後」という事象の条件付き確率は高くなるのでダメ。)
順列に対する確率の評価は、「$n$ 個とったとき、$1$ 位、$2$ 位、…、$n$ 位である確率は等確率」に基づくことが多いです。もっと解き慣れれば反応が速くなりそうかな?
各スライムごとに、各線分の使用確率が分かったので、あとはこれを線分の使用回数期待値に変換すれば答になります。
問題C – Cookie Distribution
editorials と少し違う考察な気がします。
確率変数 $X_{i,j}$ を、次で定義します:\[X_{i,j} = \begin{cases} 1 & (1人 i が j 日目に受け取ったとき)\\0 & (それ以外のとき)\end{cases}\]
このとき、$\prod_j\bigl(\sum_j(X_{i,j})\bigr)$ の期待値を計算すればよいです。
ちょっと記号がごちゃごちゃしているので、サンプル 1 を具体的に書いてみます。$X_{i,1}$ を単に $X_i$ と書き、$X_{i,2}$ を $Y_i$ と書くことにします。
\[ c_1c_2c_3 = (X_1+Y_1)(X_2+Y_2)(X_3+Y_3)\]
この期待値を計算するには、展開して、
\[ \begin{align*}E[c_1c_2c_3] &= E[X_1X_2X_3] + E[X_1X_2Y_3] +E[X_1Y_2X_3] + E[Y_1X_2X_3] \\&+ E[X_1Y_2Y_3] + E[Y_1X_2Y_3] + E[Y_1Y_2X_3] + E[Y_1Y_2Y_3]\end{align*}\]
の要領で計算します($E[X]$ は確率変数 $X$ の期待値)。
独立な確率変数に注意すると、
\[ \begin{align*}E[c_1c_2c_3] &= E[X_1X_2X_3] + E[X_1X_2]E[Y_3] +E[X_1X_3]E[Y_2] + E[X_2X_3]E[Y_1] \\&+ E[X_1]E[Y_2Y_3] + E[X_2]E[Y_1Y_3] + E[X_3]E[Y_1Y_2] + E[Y_1Y_2Y_3]\end{align*}\]
となり、さらに明らかに、$E[X_1] = E[X_2] = E[X_3]$, $E[X_1X_2] = E[X_1X_3] = E[X_2X_3]$ などが成り立ちます。
$x_0 = 1, x_1 = E[X_1], x_2 = E[X_1X_2], x_3 = E[X_1X_2X_3]$ とします。$y_0 = 1, y_1 = E[Y_1], y_2 = E[Y_1Y_2], y_3 = E[Y_1Y_2Y_3]$ とします。
\[E[c_1c_2c_3] = x_0y_3 + 3x_1y_2 + 3x_2y_1 + x_3y_0\]
と計算できて、これで サンプル 1 がそれっぽく計算できました。
日数が増えても同様です。多項式の積 $\prod_{j=1}^k\bigl(\sum_j(X_{i,j})\bigr)$ を展開したとき、
・$k$ 日目までみて、$n$ 個の変数の積の期待値の総和が $f_{k,n}$ とする
・$k+1$ 日目だけを考えて、$n$ 個の変数の積の期待値が $g_n$ とする
・$f_{k+1,n} = \sum_i\binom{n}{i}f_{k,i}g_{n-i}$ の要領で $f$ を更新していく
と計算すればよいです。なお、
$\frac{f_{k+1,n}}{n!} = \sum_i\frac{f_{k,i}}{i!}\frac{g_{n-i}}{(n-i)!}$ と書いてみると畳み込みの形になっているので、FFT を利用して $\Theta(KN\log N)$ の計算量で解くこともできます。(私の提出 → ■)
問題D – Arrangement
基本的には、最後の数手で調整できそうな気がします。
はじめ、最後の 3 手で必ず調整できそうな気がしました。反例を見つけたものの、4手あればできそうな気がして、これを全探索で確かめます。
先頭に置けない数値は 1 つ決め打つ。残った数値間の禁止ルールとしては、$4! = 24$ 通りあって……。
ここでミスしていました。$4^4 = 256$ 通り(あるいは自己ループを除けば $81$ 通り)を探索することが必要です。
「貪欲にとって、最後 4 手で全探索して解く」を実装して提出 → ■(RE)
お行儀悪いですが、REとWAの出し分けなどを利用して、バグ箇所を特定します。どうやら、「最後 4 手で全探索」で、「解なし」が出ているようです。
※ 10分+6 提出ほどかかっています、手際がわるい…
※ 巨大なランダムケースでもREが出ず。
※ 小さい場合のランダムケースでもREが出ず。ここもpermutationで作ってたw
なぜ…。もう 1 回、「4手全探索」を確認します。問題文と往復しながら、いつの間にか $A$ を順列にしていたことに気づきます。
「全員から嫌われている人が居る場合にアウト」に気づきます。あとは、それを避けることが必要十分であることなどを検証し、実装。
「in_degの最大値」をheapq・setで管理しました。「全員から嫌われている人が現れた」ときの処理としては、まずはその人を左端に置いたあと、再び貪欲に並べていくことになります。ここを突貫工事で別関数に逃がすなどして…。
実装にあとから分かりにくく手を加えていって、いかにもバグらせそうな実装でしたが、何とかACを得ました。

