
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | |||
| 結果 | AC | WA | AC |
レーティングの節目を 1 つ超えました。これまでの総括記事 → [AtCoder] 橙(2400+)になりました
全体感想
115分2完で、74位でした。
レーティングの節目を 1 つ超えました。これまでの総括記事 → [AtCoder] 橙(2400+)になりました
ひらめきよりも、論理だてた考察が実を結びやすそうな、問題Dを考えました。2時間近くかかってしまいましたが、きちんと仕留め切れてよかったです。制限時間がこわくて、少しバグはまりすると 1 完になるところ…まだまだ安定度のない危うい戦いが続きます。
ラスト30分は、問題文を見た印象ではなく、順位表から判断して、問題Bと戦いました。あと一歩詰め切れずでした。ソースコード上では、ほんの 1 行書き加えればACになるくらいのところまで行っていました。問題C, E, Fはほとんど考えることも出来ず(>_<)
順位としては、問題Cがいつもより難しかったっぽいおかげで、2完しかできていないながらも良いパフォーマンス値でした。でも、問題Bをあと一歩詰められていれば、過去最高順位取れていたらしいので、もっと上を見たくなってしまいますね。
次は2800+を目指していくことになるので、Perf 2700 はやや失敗と認識していかなくてはいけません。3000+の当たり回も1つでも多く作っていきたいところで、今回のようにチャンスがあった回を1つ落としてしまったのは実際、悔しいところです(>_<)
たまに当たりを引ける実力はついてきているように思えてきたので、引き続き頑張ります。
問題A – ><
問題名がかわいい。
解説pdfと同様の考察ルートをとりました。
「$a > b < c$ のとき $b=0$ としてよい」を考察の起点とする方が自然だったかも (>_<)
問題B – Two Contests
どんどん生存者が減っていくため、全探索っぽくやっても状態数は少ないかも → サンプル 1 を書き出す → やっぱり難しい。
最終的に生き残る区間を固定すると、実現可能かは貪欲に判定できそう → これも計算量が大きい → しかし、何らかの貪欲手法が使われる問題だと感じる
サンプル 1 をもう少し観察して、より良い貪欲構成を探ります。例えば、
・コンテスト 1 → [1,2,3,4]
を決め打ちます。サンプル 1 の観察では、「[5,6,7,8] はコンテスト2としてよさそう」が分かります。実際、これらを同日に配置すると、1日分は捨てることになってしまいます。この場合は簡単で、「1日捨てて、2日目に適切な1問だけを置く」をすればよいことになります。
・コンテスト 1 → [1,2,3,4], コンテスト 2 → [5,6,7,8]
を決め打って、残りの戦略を考えます。まだちょっと戦略が決まらないです。ここで「最終的に残す区間を固定すると貪欲」を思い出します。
・コンテスト 1 → [1,2,3,4] のうち全員を生存させる
・コンテスト 1 → [1,2,3,4] のうち [1] を見捨てる
・コンテスト 1 → [1,2,3,4] のうち [1,2] を見捨てる
・コンテスト 1 → [1,2,3,4] のうち [1,2,3] を見捨てる
等で場合分けをしてあげると、残った区間のうちコンテスト 1 でどれを使うべきかが決まっていきます。すると、使う区間の集合は、「左端座標でソートしたときの、ある番号まで」の形をしていることが分かり、$O(N)$ で全ての候補を試せるようになります。
細部を詰めていきます。今回、2つの交わりのない区間を起点として考察を進めました。これを一般化します。
(1) $R$ が最小の区間 $I_1 = [L_1,R_1]$ をとる。$L$ が最大の区間 $I_2 = [L_2,R_2]$ をとる。
(2) $I_1 == I_2$ な場合 → これは包含について最小の区間。 → この場合の考察は容易。
「単一の最長区間を使う」「残りの区間を全部まとめて使う(最小区間が生存)」。
(3) $I_1,I_2$ が交わらなければ、サンプル 1 での考察が活きそう。交わるときを考える。この2つの区間が交わるとき、全ての区間が交わる。この交わりの人間たちは、自動的に2日とも全問正解するので、無視して戦略を組み立てても良いだろう。よって、交わりのない区間 $I_1,I_2$ がとれているとして戦略を組み立てればよい。
(4) $I_1,I_2$ が同一開催のときは、片方のコンテストを捨てることになる。片方に最長区間を置いて、残りに他の問題を固めればよい。
(5) $I_1$ を1日目として、$I_2$ を2日目とする。残りの区間を左端でソートして、$I_3,I_4,\ldots$ とする。このとき、各 $n$ に対して「$I_3,\ldots,I_n$ を1日目、$I_{n+1},I_{n+2},\ldots$を2日目」とする戦略を全てテストすればよい。
考察の概形ができた時点で、22:15を過ぎていました。慌てて実装します。残り時間7分で提出。2ケースのみでWAを出していました。
原因は、(3), (4)の部分の処理にあって。「戦略を組み立てる際に、全区間の共通部分の人間は無視してもよい」は正しいのですが、答を出す時点でまで無視してはいけません。(4) の処理を、「戦略を試す」ではなく「最長区間長を答として返す」としていたため、ここの値がずれていました。
残り5分。いま思えば思いつける範囲であったと思いますが…。時間に追われて、考察の細部をここに記述したほど整理しないままの実装になってしまったので、残り5分では何をすれば良いのか分からなかったです(考察の大筋レベルでの見落としがないかどうかすら、確証がなかったため)。
$>$ を $\geqq$ に変えたり、ソート関数を適当に少し変えたパターンをたくさん投げるも実らずw
悔しいところですが、残り時間の兼ね合いを考えるとこの問題についてはまぁ十分な努力が出来ていて、本問の立ち回りよりは実力不足(Dが遅い)での仕方のない範囲かなという気がします。
問題D – Balance Beam
「勝率が最大となる並び」を問われていますが、まずは台の並びを固定したときに、「勝率の求め方」を整理する必要がありそうです。入力例をいじりながら考えます。
まず簡単な気づきとして、すぬけの勝利する場合のりんごの位置は、「左端から一定距離以内」という範囲になります。つまり、確率を調べるためには、「ぴったり勝敗の分かれる境界の位置」だけを考察すればよいと分かります。この境界の位置において、「ぎりぎり追いつくもののそれ以上の余裕はない」ことから、「ぴったり台の境界で追いつく」ことが分かります。
例えばサンプル 2 の4つの台をこのまま順で並べたときの、「ぴったり台の境界で追いつく」ような出発地点は下の図のように求められます。
※ すぬけ → 追いつく時刻が決定できる → りんご → その場合の出発地点が分かる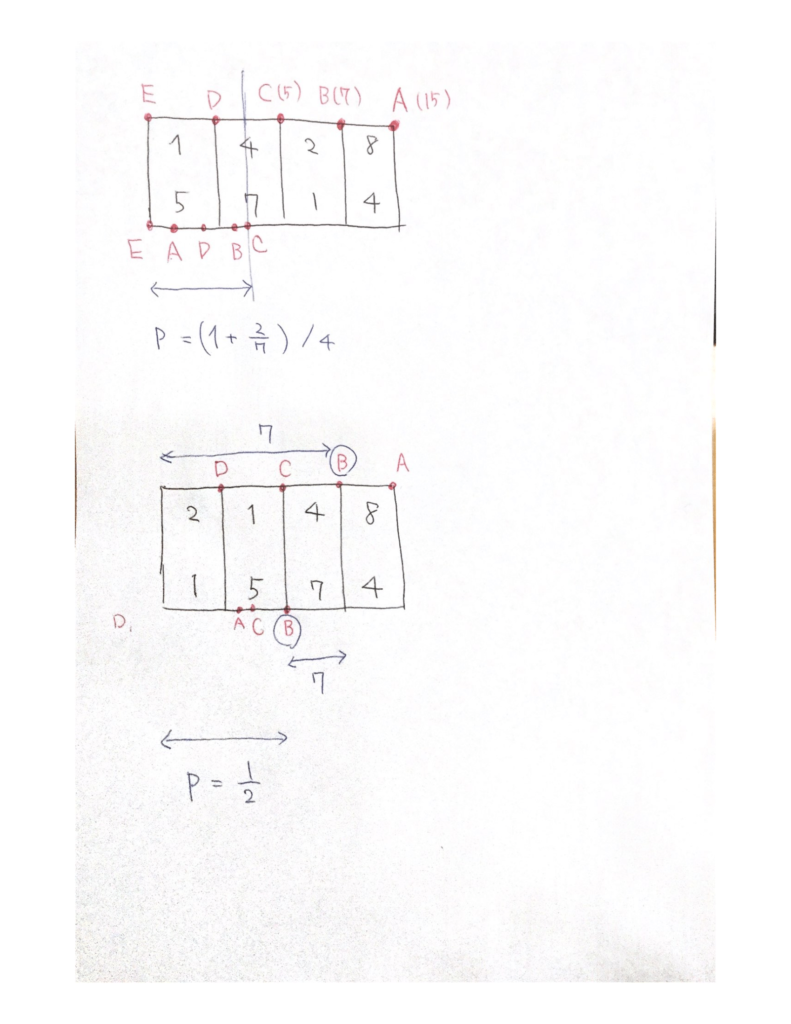
サンプル 2 の解は、例えば台 3, 1, 2, 4 の順に並べることで、上図のように達成できます。
勝率の計算が少しずつ理解できてきました。ここから、最適な「平均台の並べ方」を絞り込んでいきます。最適解の完全な決定が出来なくても、最適解に何らかの構造さえ見いだせれば、探索すべき状態が少なくなるはずで、この辺は過去問の経験から学んだ考え方です。
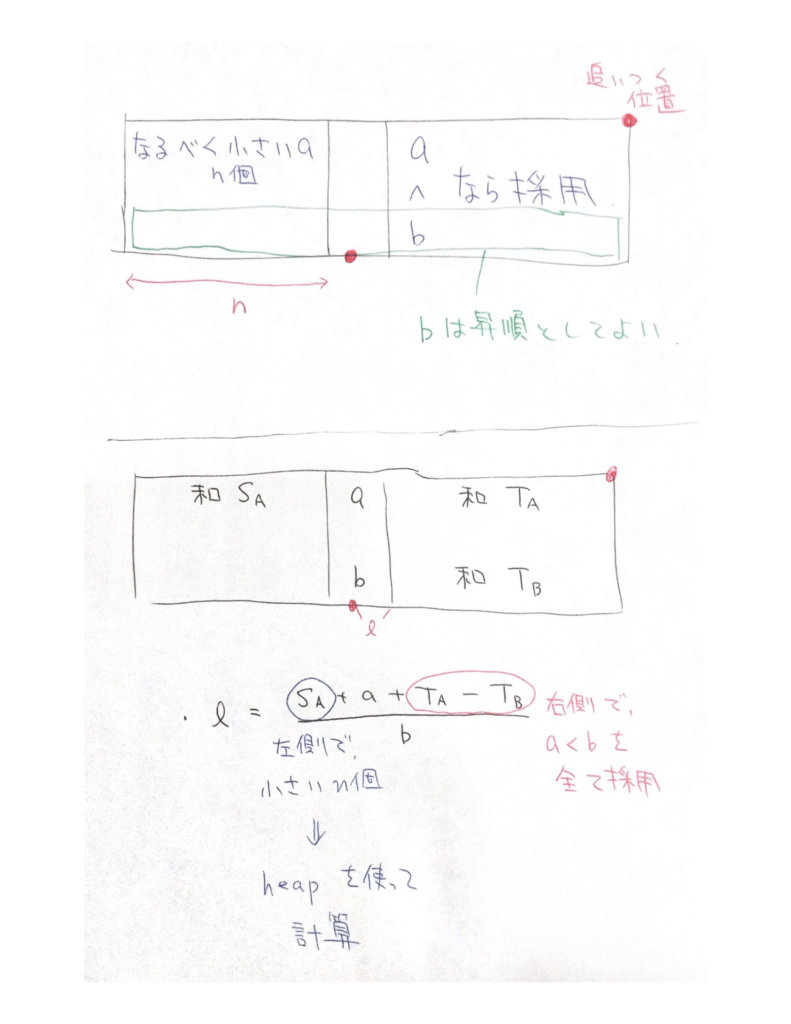
とりあえず、最適解の場合の「出発位置」「追いつく位置」が分かっているかのような図を描いてみます。「追いつく位置」よりも右側の平均台の並び順は、一切考慮する必要はありません。
・「追いつく位置」の左側の $a$ の値の総和が、「追いつく時刻」を決定する。この計算において、$a$ の並び順は関係ない。
・したがって、「追いつく位置の左側に並ぶ平均台の集合」を決め打った場合、並び順は $b$ 側の都合だけで決めてしまえる。
・りんごさんがなるべく少ない距離しか進めないようにしたい。したがって、大きい $b$ ほど「出発位置より右側」に配置すべき。
・よって、最適解の構造として、$b$ は(「追いつく位置」までの間)昇順に並んでいるとしてよい。
ここから先は、パラメータが多すぎてよくわからなくなるので、なるべくきちんと数式を作っていきます。りんごさんの出発位置について計算式を作ります。すると、「出発位置の右側には、追いつく位置までに $a<b$ となる平均台をなるべく多く配置すべき」と分かります。最適解の候補を挙げるために与えるべきパラメータが 1 つ減って、出発位置となる平均台 $(a,b)$ さえ決めれば、右側の配置(追いつく位置)が決まってしまうことがわかります。
この範囲での $a$, $b$ の和を $T_A$, $T_B$ とします。この値は出発位置として決め打つ台 $(a,b)$ を固定すると事前計算できることが分かります(実際には $T_B – T_A$ だけが必要)。
左側が面倒です。勝率には「左側の台の個数」「$S_A$(左側の $a$ の和)」という2つの量が関係してきそうです。そこでさらに、台の個数 $n$ も決め打ってみます。$S_A$ はなるべく小さくした方が良いので、$(a,b)$ の左側に配置できる台のうち、小さいものから $n$ 件を選ぶのが正しいと分かります。
結局のところ、
・勝敗の境界となる出発位置の平均台 $(a,b)$
・その左側に並ぶ平均台の個数 $n$
が決まれば、そのような状態がありうるか / その場合の勝率、が計算できます。これだとまだ $\Theta(N^2)$ 件の計算を行わなければいけないようですが、$n$ について二分探索することで、必要な計算件数が $\Theta(N\log N)$ 件に落ちます。よって大体解けました。
台を動かしながら動的に $S_A$ を求めるところでは、heap を使って、「これまで見た数のうち最小 $n$ 件」を動的に管理していきます。heap の管理に $O(\log n)$ かかるため、二分探索と合わせて $O(N(\log N)^2)$ 解法として提出しました。公式解説よりも、log 1つ分悪いですが、ACすることができました。

