概要
問題文 → ■
公式解説 → 存在するか分からず
自分の提出 → ■
解法
$s, t$ などと書くと経路を表すことにします.$\mathrm{prob}(s)$ などと書けばその経路の実現する確率とします.$\mathrm{same}(s,t)$ は,$s,t$ が定める文字列が等しいならば $1$,そうでなければ $0$ とします.
$f(s) = \sum_{t}\mathrm{same}(s,t)$ です.求めたいものは
$\sum_{s,t}\mathrm{prob}(s)\mathrm{same}(s,t)$
です.
$s, t$ を同時に $1$ マスずつ進めながら dp すれば,これを求めることができます.
簡単のため,グリッドを変形して進行方向は下または右下であるとします($i$ 文字目に通るマスが $i$ 行目に来るようにする).
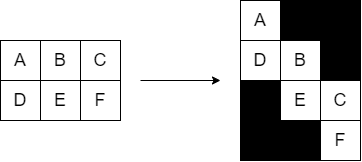
次のような dp[i][j][k] を考えます:
- $(i,j)$ までの経路 $s$,$(i,k)$ までの経路 $t$ の組であって,そこまでの文字列が same なものに対する prob(s) の総和.
状態数 $O((N+M)M^2)$,$s, t$ の $2$ 通りの進み方を試す感じで $O(1)$ 通りの遷移で計算できます.計算量 $O((N+M)M^2)$ で解けます.
計算時点で最も大きな $i$ に対する dp[i][-][-] しか保持する必要がないため,空間は $O(M^2)$ で実装できます.

