概要
公式解説の理解に失敗しましたが,たぶん別解法っぽいので一応書いておきます.
解法
$z$ 方向には座圧しておきます.$z$ での断面を考えます.
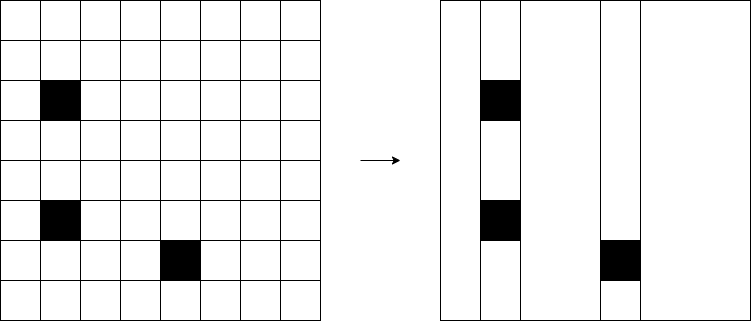
各断面は $x$ 方向に座圧して,適当な方法で長方形に分割します.
断面に除外立方体が $n$ 個あるとすると,各断面は $O(n)$ 個の長方形に分割されます.これで,$O(N)$ 頂点のグラフに対して連結成分分解をするという問題に帰着されました.
隣接関係は,同じ断面の中での隣接と,$z,z+1$ での断面の間での隣接関係があります.同じ断面の中では,$x,x+1$ の間での隣接をとればよく,尺取り法のように行えます.
断面の間での隣接関係は,まず 2 つの断面の共通の細分をとります.これは,除外長方形の和集合を除外長方形として最初の長方形分割の計算をすればよく,同じ実装を使いまわすことが可能です.細分された長方形のそれぞれから,上面・下面の長方形を見て,どちらも除外されていなければそこに辺を張っていきます.
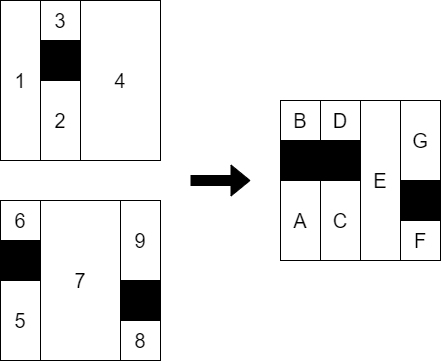
上図でいえば,共通の細分が道側で, A の上下のノード (1,5),B の上下のノード (1,6) などの間に辺を張っていくことになります.細分にとっているため,「A の上」「A の下」などは一意です.
全部で $O(N)$ 回の長方形の生成やソートの類を行うため,全体の計算量は $O(N\log N)$ 時間です.

