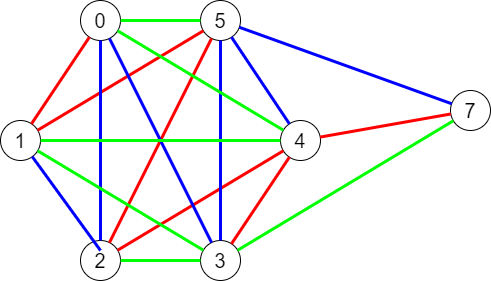
概要
問題文 → ■
公式解説 → なさそう?
ジャッジが壊れている問題です。2021 年 4 月現在、AC が不可能だと思います。
解説がなさそうだったので書きますシリーズ。
解法
上からの評価
$K > N/2$ ならば解が存在しません。このことは、完全グラフの辺の個数が $\binom{N}{2}$ であることと、各全域木の辺の個数が $N-1$ であることから分かります。
解の構成($N$ が偶数の場合)
$K = N/2$ に対する構成方法を述べます。$K < N/2$ の場合には、それらの全域木のうち $K$ 個を出力すればよいです。
頂点を、$0$ 以上 $N$ 未満の整数と対応させておきます。$k = 0, 2, \ldots, N-2$ に対して、
- $x\neq y$ は、$x + y\equiv k\pmod{N}$ または $x+y\equiv k+1\pmod{N}$ のとき、そのときに限り辺で結ぶ
としてグラフを作ります。こうしてできるグラフを $P_k$ と書くことにします。次が成り立ちます。
- 各 $P_k$ はパスである
- 任意の辺 $xy$ は、ちょうどひとつの $P_k$ に含まれる
パスであることの証明:$v$ と $v+1$ が辺を $2$ 回辿ることで行き来可能なので、連結。任意の頂点の次数が $2$ 以下なので、パスまたはサイクル。次数 $1$ の頂点があるので、パス。
$xy$ を含む $P_k$ の一意性の証明:このような $k$ は $k\equiv x+y \text{or} x+y-1\pmod{N}$ を満たすものであり、$N, k$ が偶数なので唯一である。
これで完全グラフが全域パスに分解できました。パスは木でもあるので、求めるものです。
例えば、$N=8$, $k = 0$ とすると、以下のような形になります。
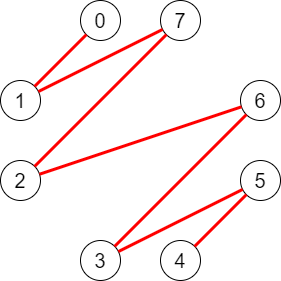
これをくるくる回していって、完全グラフを分解できます。図で見るのと数式で見るのとどちらが分かりやすいでしょう?(個人差ありそう)
$N$ が奇数の場合
$K = \frac{N-1}{2}$ 個の辺素全域木をとりましょう。今回は、すべての辺を使い切る必要はありません。
ひとつの頂点を選び、避けておきます。残った $N-1$ 点に対して上述のようにパス分解 $(P_i)_i$ を作ります。そのあと、各 $P_i$ から避けておいた点にひとつ辺を張ります。最後に辺を張る操作で辺が重複しないようにすればよく、これは容易です。
例えば $N = 7$ を、$3$ つの全域木に分ける場合、次のような方法が可能です。