続き → (2) 問題編
ネタバレに配慮して、これが使える問題をまとめたものは、別記事 (2) 扱いとしています。
実装をしている具体的なコードについても、必要であれば (2) 問題編 における解答例を確認してください。
日本競プロ界で呼ばれている名前を見たことがないので、codeforces blog 記事にならって slope trick と呼んでいきます。
過去問を見ていると、これを使えば簡単というものがボス問として配置されていたり、AC 人数が少なかったり、解説が別方針で難解に見えるものだったりすることが多いように感じられました。典型テクとして紹介している日本語の記事の類もほとんど見かけない気がしたので、私の方で軽くまとめてみることにしました。
参考文献
ei1333 さんによる実装例
https://ei1333.github.io/library/structure/others/slope-trick.hpp
https://ei1333.github.io/library/structure/others/generalized-slope-trick.hpp
区分線形凸関数
区分線形凸関数
slope trick とは、連続関数 $f\colon \R\longrightarrow \R$ であって、次の条件を満たすものを良い感じに管理するテクニックです。
【条件】$f$ のグラフは、左から順に傾きが $l, l+1, \ldots, r-1, r$ の線分をこの順につないだ折れ線である。(※ ちょっと雑な表現をしています。)
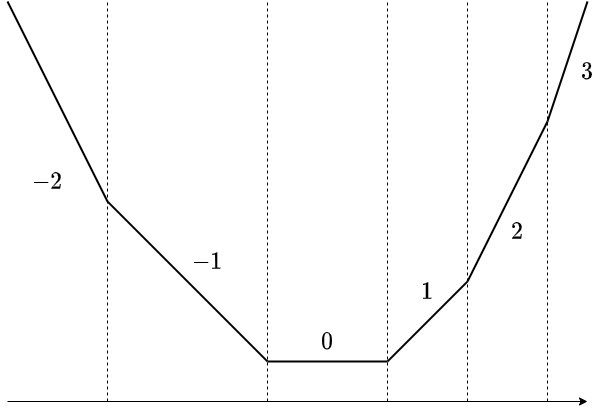
こんなやつです。傾きが $-2, -1, 0, 1, 2, 3$ の線分を結んでいます。線分といいつつ、両端は半直線ですが、面倒なのでそれも含めて「線分」と記述します。
また、都合上 長さ $0$ の線分も考える こととしておきます。
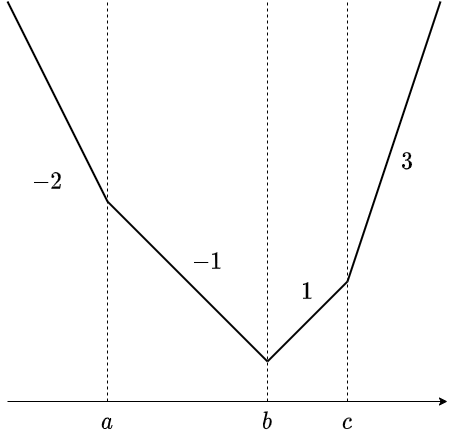
上の図では、
- $(-\infty, a]$ において傾き $-2$
- $[a,b]$ において傾き $-1$
- $[b,b]$ において傾き $0$
- $[b,c]$ において傾き $1$
- $[c,c]$ において傾き $2$
- $[c,\infty)$ において傾き $3$
の線分が、この順につながっていると見なすことにします。結局傾きが飛び飛びになる場合も考察対象に含めているということになりますね。
以下、このような関数を区分線形凸関数と呼ぶことにします。傾きの整数性を要求しているので、厳密には区分線形凸だけでは不足していますが、この記事においては混乱は生じないと思います。ご了承ください。
具体例
次の関数は、区分線形凸関数です。
- $|x|$ の平行移動 $f(x) = |x-a|$
- $f(x) = \max(0, x-a)$ の形の関数。以下これを $(x-a)_{+}$ と書くことにします。
- $f(x) = \max(0, a-x)$ の形の関数。以下これを $(a-x)_{+}$ と書くことにします。
特に重要な、後半の $2$ つを可視化しておきます。これらは $|x-a|$ の左半分・右半分といった関数で、$|x-a| = (x-a)_{+} + (a-x)_{+}$ が成り立ちます。
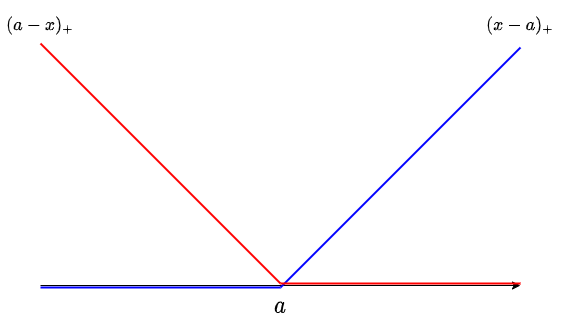
また、区分線形凸関数の和は区分線形凸関数であることも分かります。したがって、例えば $f(x) = \sum_{i} |x-a_i|$ といった関数は区分線形凸関数になります。
データの持ち方
slope trick とは、区分線形凸関数を、傾きの変化点の多重集合に置き換えて管理することで、特定の関数操作が簡潔に行えるようにするものです。
データの細部にはいくつかのパターンが考えられそうで、例えば https://codeforces.com/blog/entry/77298 では変化点と、$x\to\infty$ での様子で関数を記述する試みも見られます。今回は、私なりに考えて扱いが簡単だと思ったものを紹介します。
データの持ち方
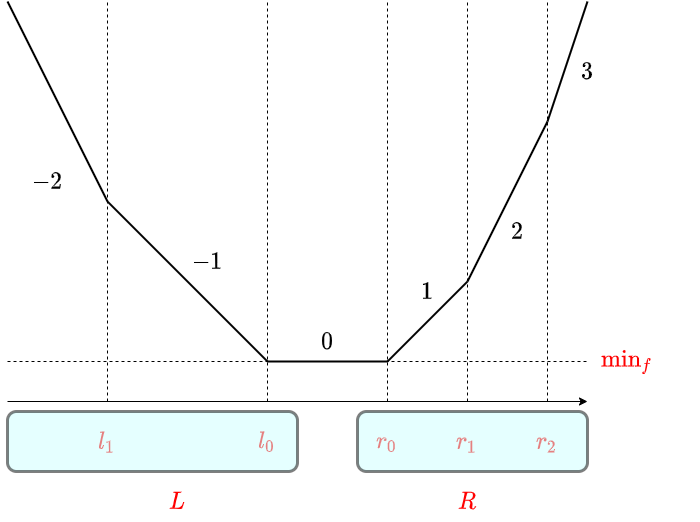
区分線形凸関数 $f$ について、次の $3$ つの情報を持ちます。
- $\text{min}_f$:$f$ の最小値
- $L$:傾きが $0$ 以下の部分について、傾きの変化点全体の多重集合
- $R$:傾きが $0$ 以上の部分について、傾きの変化点全体の多重集合
以下常に、$l_0$ と書けば $L$ の最大値、$r_0$ と書けば $R$ の最小値を表します。また、$L$ や $R$ が空の場合には、$l_0 = -\infty$, $r_0 = \infty$ と定めます(明示的に番兵を入れても良いでしょう)。「多重集合」の持ち方としては、優先度付きキューを用いて、$l_0, r_0$ が常にとれるようにすることを想定します。
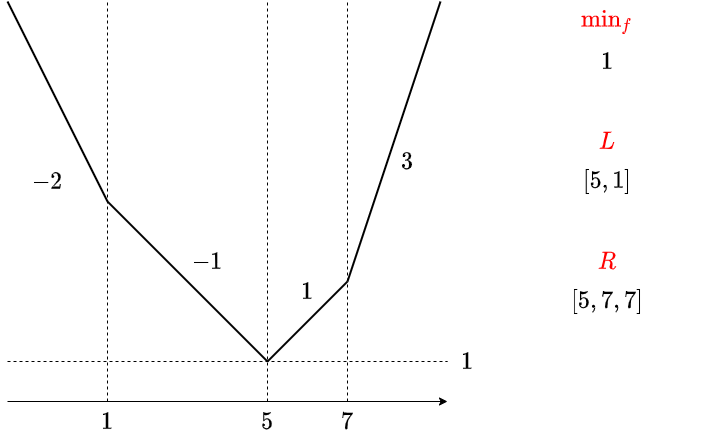
傾きが $2$ 以上変化する場所がある場合の例です。
復元
上のデータの持ち方をすると、$f(x)$ は次のように表すことができます:
$$f(x) = \text{min}_{f} + \sum_{l\in L} (l-x)_{+} + \sum_{r \in R} (x-r)_{+}$$
実際、左辺と右辺で
- いたるところ傾きが等しいこと
- $x\in [l_0,r_0]$ における値が等しいこと
を確かめればよいですが、どちらも容易です。
可能な操作
$N = |L|+|R|$ とします。このとき、以下の操作、計算量を実現できます。
最小値の取得:$O(1)$ 時間
$\min_{x\in \R} f(x)$ および、それを実現するような $x$ を答えることが、$O(1)$ 時間で行えます。そもそも $\text{min}_f$ を管理するという話でしたから、最小値はそのまま返すだけです。最小値をとる $x$ の範囲は、傾き $0$ の区間 $[l_0, r_0]$ で、これは優先度付きキューの先頭を読むだけなのでやはり $O(1)$ 時間で取得できます。
定数関数 $a$ の加算:$O(1)$ 時間
$\text{min}_f$ に $a$ を加えるだけです。当たり前ですね。
$(x-a)_+$ の加算:$O(\log N)$ 時間
これを加算すると、傾きの変化点に $a$ が追加されます。また、傾きの最小値は不変、最大値は $+1$ されることから、$L$ の大きさは変わらず、$R$ の大きさは $1$ 増えます。したがって、多重集合 $L\cup R\cup \{a\}$ を、小さい方から $|L|$, $|R|+1$ 元ずつに切り分けて、改めて $L$, $R$ とすればよいです。例えば次の手順で更新できます。
- $L$ に $a$ を push する。
- $L$ からひとつ値を pop してきて、それを $R$ に pushする。
$a > l_0$ のときにははじめの push は無駄となるので、$a$ と $l_0$ の大小関係で場合分けしても構わないです。あるいは、優先度付きキューの操作として、push / pop をまとめて行うメソッドがあれば、$a > l_0$ の場合にもほとんど無駄は生じません。例えば python の標準ライブラリ heapq であれば、heappushpop / heappush を一度ずつ呼ぶ形で実装できます。
$L$, $R$ の更新方法は分かったので、次に$\text{min}_f$ の更新を考えましょう。$a$ の位置で場合分けが出て面倒そうにも感じられますが、実は簡単です。更新前の $f$ における $L$ の最大値 $l_0$ に注目します。
実は、更新後も $l_0$ は最小値を与える点です。実際、$a$ の挿入により $l_0$ の前後における傾きは、$+0, +1$ のどちらかの変化をします。更新前には傾き $-1, 0$ の境界点が $l_0$ でしたから、更新後には傾き $-1, 0$ または $0, 1$ の境界点です。よって、$\text{min}_f$ の変化は $f(l_0)$ の変化に等しく、
- $\text{min}_f \leftarrow \text{min}_f + (l_0-a)_+$
とすれば、最小値の更新も完成です。
$(a-x)_+$ の加算:$O(\log N)$ 時間
同じです。
- $\text{min}_f\leftarrow \text{min}_f + (a-r_0)_+$
- $a$ を $R$ に push
- $R$ からひとつ値を pop してきて、$L$ に push
とすればよいです。
$|x-a|$ の加算:$O(\log N)$ 時間
$|x-a| = (x-a)_+ + (a-x)_+$ でしたから、上の $2$ つの操作をともに好きな順序で行えばよいです。
累積 min:$O(1)$ 時間
つまり、$g(x) := \min_{y\leq x} f(y)$ として、$f$ を $g$ に取り換える操作です。
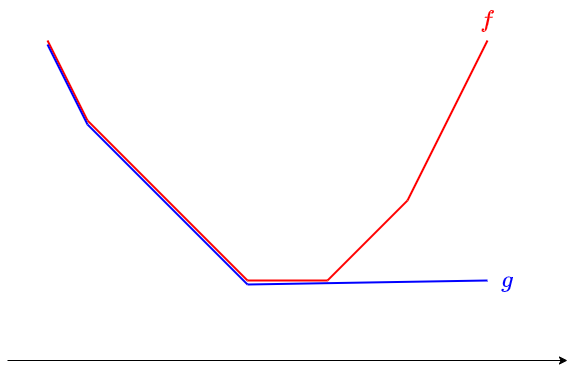
$R$ を空集合に取り換えればよいですね。
右側累積 min:$O(1)$ 時間
$g(x) := \min_{y\geq x} f(y)$ として、$f$ を $g$ に取り換える操作です。
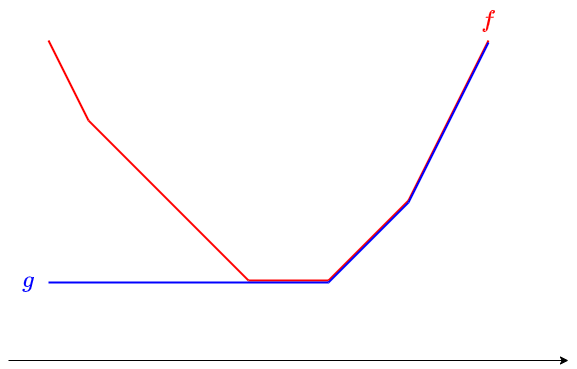
$L$ を空集合に取り換えればよいですね。
拡張
データ構造にさらに付加情報を持たせると、より多くの操作が行えるようになります。具体的には、$\text{min}_f$, $L$, $R$ に加えて、左側に一斉にで加算される値 $\text{add}_L$, 右側に一斉に加算される値 $\text{add}_R$ を持たせることにします。
挿入や取り出しをする際に、実際の値と $L$, $R$ に入れている値の差分を気を付けながら操作をします。このようにすることで、左側集合・右側集合全体への加算を $O(1)$ 時間で行えるようになります。
どのような操作が可能になるかを確認しておきましょう。
平行移動:$O(1)$ 時間
区分線形凸関数 $f(x)$ があるときに、$g(x) = f(x-a)$ となる関数 $g$ を求めることを考えます。
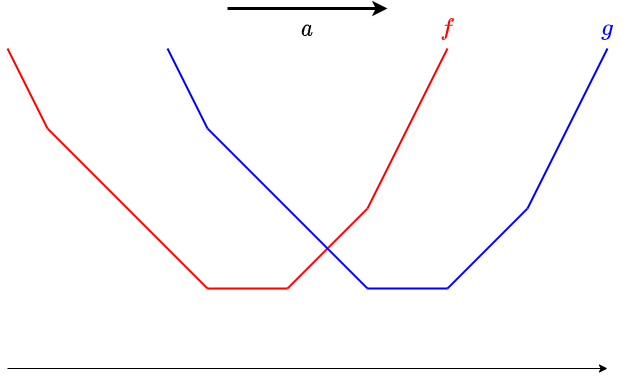
集合 $L$, $R$ に一斉に $a$ を加算すればよいです。
スライド最小値関数:$O(1)$ 時間
名前これでいいかな。sliding window minimum をとる操作です。
$a \leq b$ のとき、$$g(x) = \min_{y\in [x-b,x-a]} f(y)$$ で定まる $g$ を計算します。これは実は、左側集合・右側集合それぞれを平行移動することと対応します。
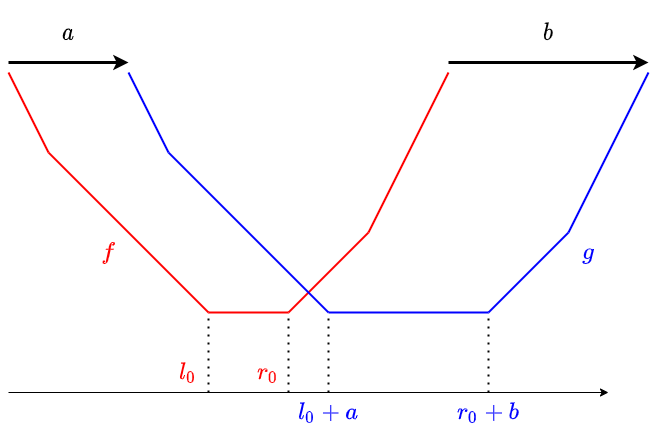
$a$ 以上 $b$ 以下の平行移動すべてに対する min をとるということで、図形的に考えても納得できるのではないでしょうか。念のため、数式で理解しておきます。
- $x\leq l_0 + a$ ならば、$x-a\leq l_0$ より $[x-b,x-a]$ において $f$ は単調減少。よって $g(x) = \min_{y\in [x-b,x-a]}f(y) = f(x-a)$
- $x\geq r_0 + b$ ならば、$x-b\geq r_0$ より $[x-b,x-a]$ において $f$ は単調増加。よって $g(x) = \min_{y\in [x-b,x-a]}f(y) = f(x-b)$
- $l_0+a\leq x\leq r_0+b$ ならば、$[x-b,x-a]\cap [l_0,r_0]\neq \emptyset$ なので、$g(x) = \text{min}_f$
となって、確かめられました。
なお、平行移動はこれの $a = b$ の場合と見なすことができます。
また、累積 min をとる操作は、$b = \infty$ の場合と見なすことができます。とはいえ、$\infty$ を何度も足したり引いたりするのは演算が怪しくなりますし、$\infty$ を十分大きな定数に置き換えて実装する場合にもオーバーフローや計算誤差の懸念が生じるため、素直に $R$ を空にする実装をするのが良いかと思います。
続き → (2) 問題編

