連続する1の数え上げ
$0$, $1$の2値からなるarrayがあるときに、連続で並ぶ$1$の個数を数えてみましょう。
つまり、次のような入出力を実現する方法を考えます。
入力: x = [0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0]
出力: y = [0, 4, 4, 4, 4, 0, 1, 0, 0, 2, 2, 0]それぞれ、連続で並ぶ$1$の個数を集計しています。この値は各セルの左だけを見ても求まらないので、左右からarrayを走査する必要がありそうです。より詳しくは、各セルの左右にある最も近い$0$の位置を計算してあげることを目指してみます。
入力 : x = [0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0]
左の0: left = [0, 0, 0, 0, 0, 5, 5, 7, 8, 8, 8,11]
右の0:right = [0, 5, 5, 5, 5, 5, 7, 7, 8,11,11,11]各セルから左側にある$0$の位置を取得するには、次のようにすればよいです。

インデックス$n$の位置が$n$であるようなarrayはnp.arange() により生成できます。そこから興味のないセルを$0$に書きなおします。さらに左から累積最大値をとってやれば、直前の$0$の位置が取得できます(np.ufunc.accumulate()を利用)。
実際の思考順としては、この計算を遡るような形で、その成果物を1発で得るには何が準備してあれば良いのかを、順に考えていくことになると思います。1元1元を見ながら条件分岐するようなループ処理を回避するために、「全要素に対して同じことをやる」「特定条件を満たす全要素に対して何かをやる」という操作に分解できると、numpyのパフォーマンスが十分に発揮できると思います。
逆順に並べ替えて、同じことをやってあげれば、右側の$0$の位置が取得できることになります。
逆順ソート後のインデックスを元に戻すことを忘れないようにしましょう。

計算したいものが計算できましたね!
参考1:1の個数の列だけが欲しい場合
0 が格納されているインデックスの列を取得し、差分をとれば、$0$と$0$の間の$1$の個数が取得できます。

参考2:いろいろな数の連続同一値を数える
次のように、各セルに対して、格納されている値の連続同一値をカウントすることもできます。
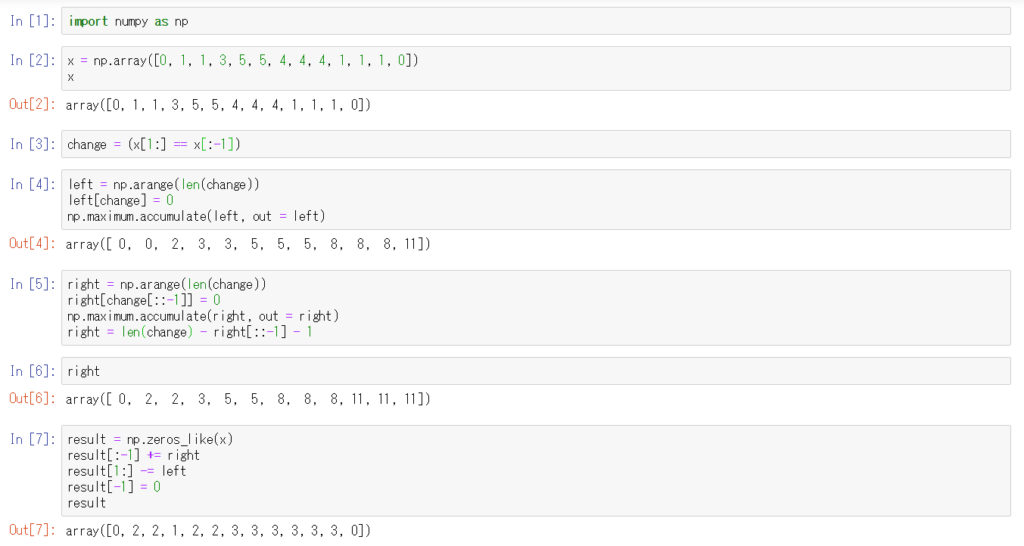
入力: x = [0, 1, 1, 3, 5, 5, 4, 4, 4, 1, 1, 1, 0]
出力: y = [0, 2, 2, 1, 2, 2, 3, 3, 3, 3, 3, 3, 0]「値の変化点」を抽出してしまいさえすれば、後は最初の例と同じように、各セルに対して左右の最寄りの変化点が求められます。「変化点」と言っても境界の左側・右側どちらのインデックスを持つことになるので、必要に応じて左右1つずらす部分が出てきます。あとは同じなので、実装例だけ載せておきます。
AtCoder ABC129 問題D
今回執筆したのは、この問題を解くときに考えた方法になります。各セルに対して、上下左右に続いている陸地の個数をカウントする問題です。安易なpythonのforループでは、実行が遅くてTLEになってしまうようです。
主要部分は上述の通りですが、軽くコード解説しておきます。
入力データの受け取り、arrayの生成
入力を受け取り、array(変数名:grid)へと変換します。障害物を$0$、それ以外を$1$として、2値のarrayを生成しています。(実際にはTrue False の2値で作成しました。)
4 6
#..#..
.....#
....#.
#.#...[[0 0 0 0 0 0 0 0]
[0 0 1 1 0 1 1 0]
[0 1 1 1 1 1 0 0]
[0 1 1 1 1 0 1 0]
[0 0 1 0 1 1 1 0]
[0 0 0 0 0 0 0 0]]外側にぐるりと1周、余計な障害物を配置しています。番兵法など呼ばれ、
・境界付近を場合分けなしに処理する。配列外参照を防ぐ。
・結果として、ソースコードを簡略化する。if 判定が減る分パフォーマンスが良くなる。
などの利点が期待できる場合があります。
import numpy as np
import sys
buf = sys.stdin.buffer
H,W = map(int,buf.readline().split())
# 周りに壁を、0,1化、壁を0で持つ
grid = np.zeros((H+2,W+2),dtype=np.bool)
grid[1:-1,1:] = (np.frombuffer(buf.read(H*(W+1)),dtype='S1') == b'.').reshape((H,W+1))arrayの生成には、np.frombufferを使用しています。バッファから直接arrayを生成できるため、パフォーマンスが良いようです。atcoderの制約条件では、割と大きな差となります。
| import numpy するだけ | ■ | 148 ms |
| frombuffer から生成 | ■ | 196 ms |
| リスト内包表記から生成 | ■ | 565 ms |
また、番兵の配置には、np.pad()を用いる方法もありますが、私の試した範囲では、むしろパフォーマンスが悪いという結果でした。
主要な計算部分
肝心の計算部分は、横方向・縦方向に分けて行います。こうすると、本記事で述べた通りの問題になります。私の提出解答では、1次元arrayに変換してから計算していますが、これは計算量にはほとんど影響しないと思われます。
横方向の計算は、そのままnp.ravel()で1次元arrayにして計算しています。
縦方向の計算は、行列全体を転置してから同様の計算を行っています。
計算の主要部は、ほぼ本記事で説明した通りです(定数の足し引きを部分的にさぼって最後にまわしたりはしています)。

