問題概要
問題文 → ■
代入操作に特化した場合の区間作用・区間積クエリという問題です.
解法1:遅延セグメント木
ある区間をすべて $a$ で置き換えたときの区間積 $a^n$ は繰り返し二乗法で $O(\log n)$ 時間で計算でき,本問題を標準的な遅延セグメント木で解くことができます.
- 解答例(1243ms)
クエリあたりの計算量について,普通の遅延セグメント木の操作 $\Theta(\log N)$ に加えて,作用素を反映させる際に繰り返し二乗法の $\log N$ がついて,$\Theta(\log^2 N)$.問題全体の解法としては $\Theta(Q\log^2N)$ 時間ということになります.
(ところで私の提出,他の方の遅延セグメント木解法よりも妙に高速なような….なぜでしょう.要素数をモノイドに持たせるのではなく遅延セグメント木側で管理するようにすると何割か高速になるという経験は過去にあったので,ひとつはそれかなあ.)
解法2:定数区間を管理する
列を定数区間に分けて,定数区間をひとつのものとして管理することを目指します.
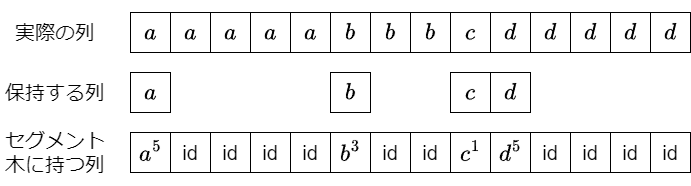
「保持する列」のインデックスは set などで管理できます.なお必要な機能は Predecessor Problem で現れるものばかりなので,64 分木や van Emde Boas Tree などの std::set よりも高速なデータ構造を利用できます.
区間積・区間代入どちらの場合でも,区間 $[l,r)$ に対するクエリ処理のはじめに,$l,r$ が列の切れ目になるように変更しておくと,比較的簡単に実装できると思います.
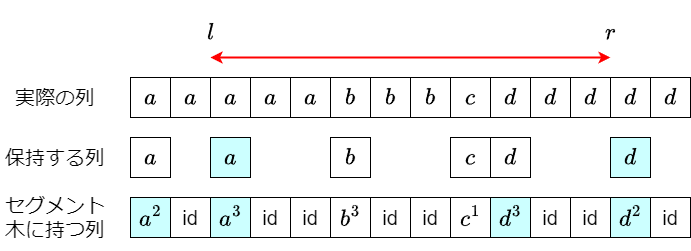
区間積を出力するにはそのままセグメント木の区間積を呼び,区間代入を行う場合には,列の $[l,r)$ 内の要素を破棄したあと左端に値を置きなおせばよいです.
- 解答例(894ms)
$Q$ 回のクエリ全体を通して,要素の追加や破棄が合計で $\Theta(N+Q)$ 回行われます.これらのたびに繰り返し二乗法を実行して,全体として計算量 $\Theta((N+Q)\log N)$ が達成できます.これは償却計算量なので永続化が難しいという,解法1 と比べた場合のデメリットもあります.
「$l,r$ が列の切れ目になるように変更しておくと,比較的簡単に実装できると思います.」と書いていたものの,いくらか無駄な pow の計算とセグ木への代入操作の回数を行ってしまってはいます.余分な操作がなくなるように実装しなおしたところ,まあまあ目に見えて高速になりました.
- 解答例(490ms)
その他の解法
本問題でクエリあたり $O(\log N)$ の時間計算量を達成する方法は,私が解説したもの以外にもいくつか発見されています.
- https://noshi91.hatenablog.com/entry/2019/10/05/203704 (noshi さん)
- 解答例(516 ms, noshi91 さんの実装例をコピペして提出したもの)
- https://www.mathenachia.blog/assign-segtree-nonamortized/ (Nachia さん)
- 解答例(657ms, Nachia さん)
どこまで定数倍を詰めた実装をしているかも違いますし,テストケースに対する相性などもあると思うので,どのアルゴリズムが優れているの性能比較と言えるほどのちゃんとした比較ではないと思います.

