問題概要
問題文 → ■
三角形内部の点の個数を数える問題です.
解法1:愚直解
$4$ 点 $A,B,C,p$ に対して $p$ が $\triangle ABC$ の内部にあるか否かを $\Theta(1)$ 時間で判定できます.すると単純なループにより本問題は $\Theta(N+MQ)$ 時間で解くことができます.実装によっては十分 AC になりますし,この解法を何らかのライブラリの verify に使ってもよいでしょう.
- 解答例 (827ms)
三角形は半平面 3 つの交わりなので,点が三角形の内部にあるかの判定は,点が半平面に含まれるかの判定 3 回により行うことができます.点が半平面に含まれるか否かの判定は,2 つの平面ベクトルの行列式(外積)の符号により判定することができます.
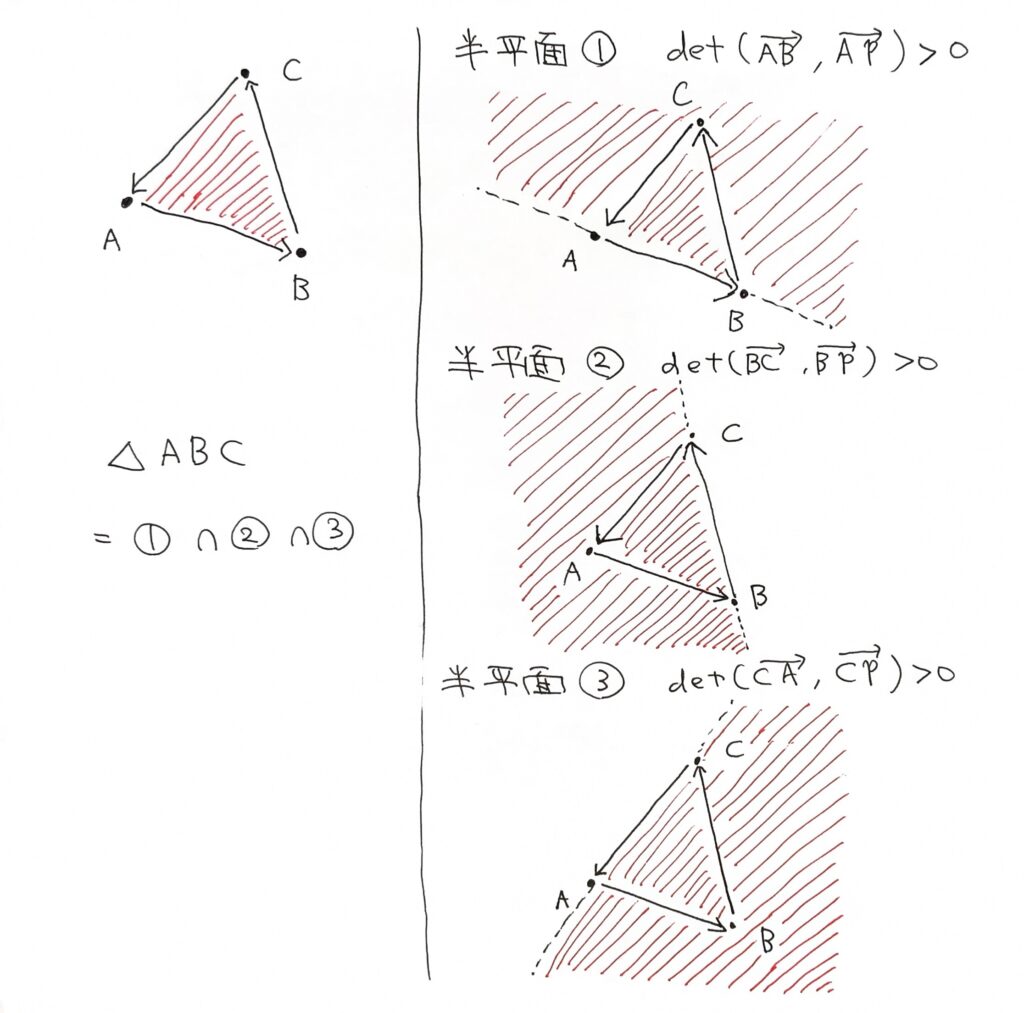
予め三角形の 3 頂点が反時計回りになるように並べておくと簡潔だと思います.また,同様の考え方によって点が凸多角形に含まれるか否かを判定することもできます.
解法2:辺ごとの寄与に分解する
三角形に対する計算を,辺に対する計算に分解しましょう.2 つの考え方を紹介します.
(1) 原点を使って三角形に分解する
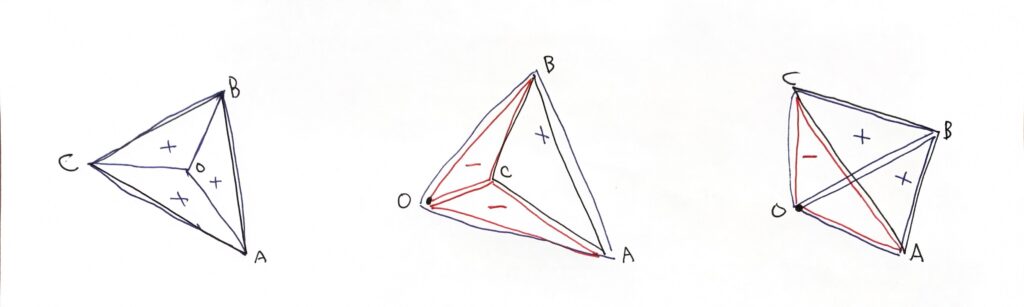
なお,適切に $x$ 方向に平行移動するなどして $O$ がどの $A_iA_jA_k$ にも含まれないようにすれば,場合分けは後者の 2 つになります.
(2) 軸に平行な直線を使って台形に分解する(Nachia さんの解法)
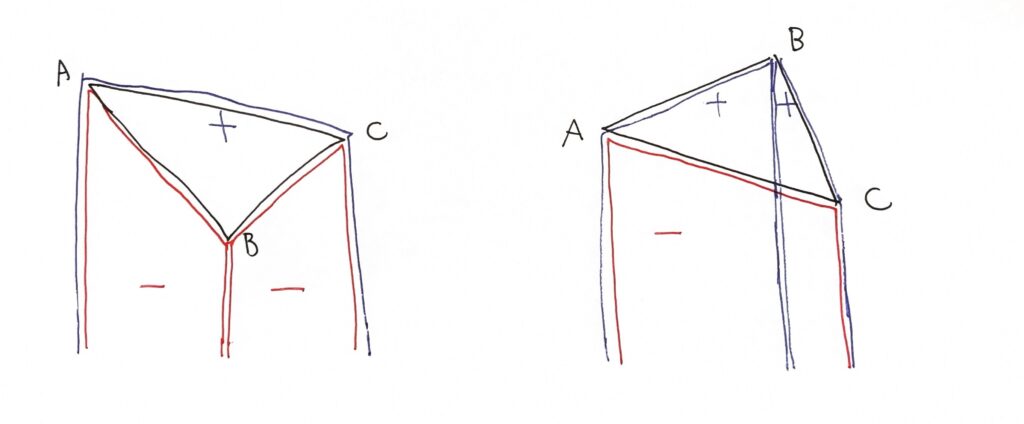
なお,この方法は,(1) において原点を $y$ 軸の負の方向の無限遠にとった場合と考えることができます.$x$ 軸方向に関する積分と考えると自然そうです.
いずれの方法でも,三角形領域を,辺によって定まる領域の和・差により表すことがほとんど正しくできています.ただし,線分 $A_iA_j$ 上の点などは慎重に使う必要があります.
結局,本問題は以下の手順で解くことができます:
- すべての辺 $A_iA_j$ に対して,その辺によって定まる領域内にある点 $B_k$ の個数を前計算しておく.必要に応じて $A_j$ と一致する $B_k$ の個数なども数えておく.
- それらを適切に足し引きすることでクエリに答える.
事前計算は単純なループで $\Theta(N^2M)$ 時間で行えます.これらを適切に実装すると,本問題を $\Theta(N^2M+Q)$ 時間で解くことができます.
- 解答例(177ms, (1) の方法)
なおこの解答例では,(1) の方法でさらに $O$ を乱択することで,すべての $A_i,B_k$ の $O$ に関する偏角が異なるようにして考察・実装をしました.
解法3:事前計算の高速化
解法2 では,すべての辺 $A_iA_j$ に対して $B_k$ を数えるという事前計算が必要でした.この部分を高速化します.
以下では解法2 (2) に基づいて説明します.
以下では簡単のため,すべての点の $x$ 座標が相異なるとして議論します.点群を $(x,y)$ についてソートしておきます.
$A_i$ を固定して,それより右側にある $A_j$ に対し,線分 $A_iA_j$ に関する前計算を行います.次のようにすればよいです.
- $A_i$ よりも右側にある点 $B_k$ を列挙し,それらを $A_i$ を基準に偏角ソートしておく.
- $x$ 座標昇順に見て,「$A_iA_j$ に対する計算」「点 $B_k$ の追加」を行う.計算では,これまでに追加された $B_k$ のうち偏角がある範囲にあるものを数えればよい.これは偏角ソートの情報と Fenwick Tree などを用いて行える.
時間計算量は $i$ を固定するごとに $\Theta((N+M)\log M)$ 時間です.本問全体の計算量は $\Theta(N(N+M)\log M+Q)$ となります.
- 解答例(110ms, Nachia さん)
解法 2 (1) を用いる場合には,$x$ 座標に関するソートを $O$ に関する偏角ソートに置き換えた上で同様の計算を行えばよいです.
- 解答例 (80ms)

