概要
問題文 → ■
公式解説 → 存在するか分からず
自分の提出 → ■
まず読解がちょっと難しかった.サンプル 1 はこんなのです.
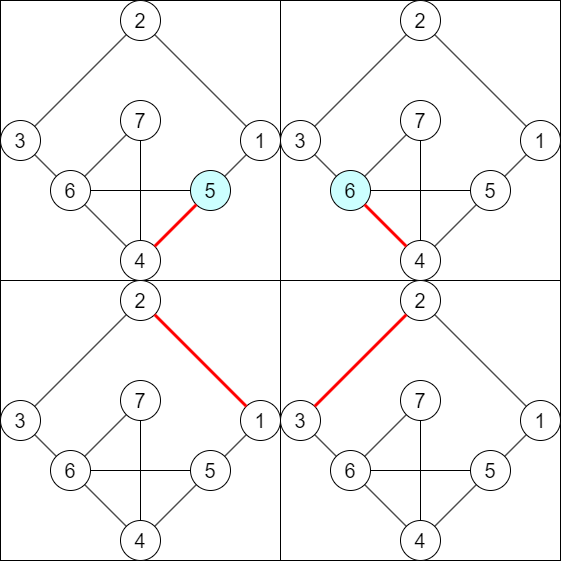
解法
同じグラフがグリッド状に並んでいて最短路問題となっています.まずひとつのグラフの中では,$4$ 方向の扉や始点・終点の距離だけが重要で,これは基本的な最短路アルゴリズムで計算可能です.
一度も壁を通らない場合をまず計算します.次に壁を通る場合について計算します.
壁を通る場合については,最初の方向と最後の方向を固定して解けばよいです.すると,次のような問題になります:
- R, U, L, D からなる文字列を最小コストで作れ.ただし,
- 先頭の文字,末尾の文字が決められている.
- R の個数と L の個数の差が決められている.
- D の個数と U の個数の差が決められている.
- 隣り合う 2 文字ごとに,コストがある.LR, DU は隣接しない.
これは,4 頂点からなるグラフに対する問題と見なせます.
つまり,
- R, U, L, D という 4 つの頂点がある.walk を最小さいコストで作れ.ただし,
- 始点,終点が決められている.
- R の出次数と L の出次数の差が決められている.
- D の出次数と U の出次数の差が決められている.
- RR, LL, DD, UU, RU, UL, LD, DR, UR, LU, DL, RD の辺重みがある.
各辺を通る回数を決めたとき,連結性と各頂点の入次数・出次数が適切になっていれば walk が作れます(Euler路).
各辺を通る回数がどうするかを考えます.
RU, UL, LD, DR 辺について,すべて 2 回以上使うならば,1 回ずつ減らした方が得です.UR, LU, DL, RD 辺についてもその通りです.
RU+UR+LD+DR という 2 つのサイクルについても,連結性を変えないまま減らせるなら減らした方が得です.RD+DR+LU+UR も同様です.
RD+DR+RU+UR というようなサイクルの 2 個組については,連結性の条件を無視すれば,2 つの RR 辺に置き換えられます.R の出次数を $+2$ する操作のコストを別に定義することにして,このようなサイクル 2 個組もなるべく消しましょう.
結局,
- 連結性を確保するためにいろいろな辺を高々 1 回使う(これは適当に十分たくさん全探索する)
- それ以外は,各点を通るサイクル,2 点を往復するサイクル,各点の出次数を +2 する操作の組み合わせで調整
という感じの計算です.もろもろ適切に実装すれば,最後には次のような問題が残ります:
- $(x,y)$ を $(+1,0), (0,+1), (+2,0), (0,+2), (+1,+1)$ する操作にコストが定まっている.$(0,0)$ から $(x,y)$ を作る最小コストを求めよ.
あとはまあまあ簡単です.
いろいろ漏れなく列挙したり,異なる始点・終点に対する実装をどう共通化するかなど,解法の方向性が分かってからきちんと実装しきるまでが結構大変だと思います.

