A – お菓子
$[x^N](x+x^3+x^4+x^6)^D$ と立式できます.
疎な fps pow なので,$O(N)$ 時間で解けます.参考
B – 整数の組
$[x^N](1+x)\cdot (1+x+x^2)\cdot \frac{1}{1-x^2}\cdot \frac{1}{1-x^3}$ と立式できます.
有理式の係数を求める問題(線形漸化式の $K$ 項目を求める問題)で,Bostan-Mori 法などで解けます.$O(\log N)$ 時間.
そもそもこの有理式が約分できて単に $[x^N]1/(1-x)^2$ となるため,答えは単に $N+1$ です.
C – 数列
$[x^S](1+x+\cdots+x^{M})^N$ と立式できます.
そのまま fps pow のライブラリを使ってもよいですし,$(1-x^{M+1})^N\cdot (1-x)^{-N}$ と式変形を使ったあと二項定理と負の二項定理を使ってもよいです.
それぞれ,$O(S\log S)$ 時間,$O(S)$ 時間で解けます.
D – 数列 2
$0\to a_1\to a_2\to \cdots \to a_N\to M$ という移動を考えると,
- 非負整数
- 正の奇数が $N-1$ 個
- 非負整数
の総和として $M$ を作る問題になります.よって
$$[x^M]\frac{1}{1-x}\cdot \left(\frac{x}{1-x^2}\right)^{N-1}\cdot \frac{1}{1-x}$$
を求める問題です.例えば真ん中の $N-1$ 乗を計算したあと累積和 $2$ 回として実装できます.
E – 数列 3
出現回数を $c_1,c_2,\ldots$ とすると,適切な範囲で $\frac{N!}{c_1!\cdots c_M!}$ を足し合わせる問題になります.適切な範囲とは,$\sum c_i=M$ かつ $0\leq c_i\leq i$ で,これを考慮すると答えは次のように立式できます.
$$N!\cdot [x^N]\prod_i \sum_{c=0}^i\frac{x^c}{c!}$$
F – 色紙
$4$ 状態の行列累乗という解法があり,それで AC 可能です.
行列累乗で解けるものは線形漸化式を持つので,行列を陽に求めずとも BMBM 法で解いてしまうこともできます.
G – 硬貨
ちょうど $n$ 円を払う方法の数え上げ $\dp[n]$ という dp テーブル($0\leq n\leq N$)を考えてある硬貨の追加・削除を行えればよいです.
削除が少し直感的に処理しにくいですが,FPS で考えれば追加は単に $\frac{1}{1-x^a}$ をかけることなので,削除は $(1-x^a)$ をかけることを実装すればよいです.
H – ジャンプ
与えられた移動ルールの母関数を $F(x,y)$ とします.$(0,0)$ も認めたものを $G(x,y)$ とします.
$G(x,y)=1+F(x,y)$ で,規則的に扱いやすいのは $G(x,y)$ の方です.
まず $b_n = [x^Ny^M]G^n$ を求めます.これは軸ごとに分けて扱えば簡単です.
$a_n = [x^Ny^M]F^n$ を求めることが目標ですが,$F^n=(G-1)^n$ より $a_n=\sum_k\binom{n}{k}b_k(-1)^{n-k}$ となって,これを整理すると $a$ は $b$ から適当な畳み込みで求まることが分かります.
指数型母関数の意味付けを考えて直接 $B(x)=A(x)e^x$ の形の立式をすることもできます.
I – スコア
$[x^K]\prod_i(1+A_ix)$ です.このような総積は,分割統治などを利用して次数のバランスを保った計算手順をとることで,$O(N\log^2 N)$ 時間で計算できます.
J – スゴロク
$i$ に到達する確率 $\dp[i]$ という dp テーブルを求めることを目標にします.NG cell からの遷移を禁止して,NG cell での dp 値の総和を求めると,失敗確率が計算できます.
dp の遷移には計算順序の自由度がいくらかあって,次を満たすような順序で処理できればよいです.
- $i<j$ となるすべての $i,j$ について,遷移 $\dp[i]\to \dp[j]$ を計算している.
- ただし,$\dp[i]$ を計算する時点で,$i$ に向かう遷移はすべて計算済である.
分割統治で計算します.$L\leq i<j<R$ を満たすような遷移をすべて行う関数を dfs(L,R) として,dfs(L,R) が呼ばれた際には
- dfs(L,M)
- $[L,M)$ から $[M,R)$ への全組み合わせによる遷移
- dfs(M,R)
を順に呼ぶというようにすれば,目的の計算手順が実現できます.真ん中の処理がサイズが $O(R-L)$ の列の畳み込みにできることから,全体では $O(N\log^2N)$ 時間解けます.
K – 順列
数え上げの関係式を得る上で,「任意のもの」を「既約なもの」に分解する様子を考えるという手法があります(後述の,連結グラフ数え上げなどもそう).
任意の順列について,「$p_l,\ldots,p_r$ は多重集合として $l,…,r$ に一致する」という $[l,r]$ を既約な区間だと考えて,既約分解を考えることができます.
$$1,2,4,3,7,5,6 → |1|2|4,3|7,5,6|$$
すると,「任意の順列」は,「$k_1+k_2+\cdots+k_m=n$ となる分割 $(k_1,k_2,\ldots,k_m)$ をとり,それぞれ長さ $k_i$ の既約な順列を定めること」と対応します.
「任意の順列」の母関数を $F(x)$ として,「既約な順列」の母関数を $G(x)$ とすれば,$F(x)=\sum_mG(x)^m$ という関係式が得られます.よって $F(x)=\frac{1}{1-G(x)}$ です.
$F(x)$ は簡単に分かるので,そこから $G(x)$ も分かります.
参考,OEIS A003319
L – 順列 2
順列を functional graph としてみて考えると次のようになります.
- $N$ 頂点の有向グラフであって,各連結成分が $3$ 頂点以上のサイクルであるものを数えよ.
これを得るには次のようにすればよいです.
- $N=k_1+k_2+\cdots+k_m$ となる $3$ 以上の $k_1,\ldots,k_m$ をとる.
- $N$ 元集合を $k_1,\ldots,k_m$ 元集合 $S_1,\ldots,S_m$ に分割する.(多項係数が登場)
- 各 $S_i$ を有向サイクルにする.
- ただし,この方法では同じグラフが $m!$ 回ずつ作られる(集合のラベルの置換).
$n$ 頂点をサイクルにする方法を $a_n$ として,$A(x)=\sum_n\frac{a_n}{n!}x^n$ とすると,答えは次のように立式できます.
$$N![x^N]\sum_m \frac{1}{m!}A(x)^m=N![x^N]\exp A(x)$$
$N!$ と,$A(x)$ の定義式の分母の $n!$ が多項係数由来です.同じグラフが $m!$ 回ずつ作られることから $\frac{1}{m!}$ が登場しています.結局 $\exp$ の計算が本質で,$O(N\log N)$ 時間で解けます.
この問題では,$A(x)=\sum_{n\geq 3}\frac{1}{n}x^n=-\log(1-x)-x-\frac{1}{2}x^2$ です.よって
$$\exp A(x)=\frac{1}{1-x}\cdot \exp\left(-x-\frac12 x^2\right)$$
なので,$O(N)$ 時間で解くこともできます.
M – 連結グラフ
$A(x)$ を連結グラフの EGF,$B(x)$ を任意のグラフの EGF とします(数え上げを $a_n,b_n$ としたときの $\sum \frac{a_n}{n!}x^n$, $\sum \frac{b_n}{n!}x^n$).
すると,L とほとんど同じように,$B(x)=\exp A(x)$ が分かります.
今回は $B(x)$ が簡単に求まり,$B$ を既知として $A$ が知りたいという状況です.これは $A(x)=\log B(x)$ と計算できます.
N – 硬貨 2
答は次のように立式出来ます:
$$[x^N] \prod_i (1+x^i+x^{2i}+\cdots+x^{iA_i})$$
これを $\frac{1-x^{i(A+1)}}{1-x^A}$ のように表すと,$(1-x^a)^{\pm 1}$ の形の FPS を $O(N)$ 個かければよいことになります.
$\log (1-x^A)$ が $N$ 次以下の項を $O(N/A)$ 個程度しか持たないから,$\log$ を求めて $\exp$ に入れるという要領で $O(N\log N)$ 時間で解けます.
O – 根付き木
根が $1$ であるという条件を無視して数えて,最後に $N$ で割ることにします.
$F(x)$ を根付き木の EGF とすると,次のように立式出来ます.
$$F(x) = x\left(1+\sum_{p}\frac{1}{p!}F(x)^p\right)$$
もちろん「$1$」の部分が,子が $0$ 個の場合に対応し,「$\frac{1}{p!}F(x)^p$」の部分が子が $p$ 個の場合に対応します.
$p$ 個の方を確認しておくと,子を $p$ 個持つ $N$ 頂点の根付き木を定めるには
- $N=1+n_1+\cdots+n_p$ と分割
- 頂点集合を $1,n_1,\ldots,n_p$ 元集合 $S_0,S_1,\ldots,S_p$ に分割
- $n_i$ 頂点集合とそれぞれを根付き木にする.
- ただしこれでは同じ根付き木が $p!$ 回ずつ作られてしまう.
という要領です.
このように「$F(x)$ の計算をしようとすると $F(x)$ が登場した」という状況は特に根付き木の数え上げでよく登場します.今回は,$G(x)=\frac{1}{1+\sum_{p}\frac{1}{p!}x^p}$ とすれば $G(F(x))=x$ という条件になるため,逆関数の計算($O(N\log^2N)$ 時間)あるいはラグランジュ反転を用いて($O(N\log N)$ 時間で))答を求めることができます.
P – ボール
答は次のように立式出来ます.
- 答は $N![x^N]\prod_{0\leq i\leq m}f_i(x)$,ただし
- $f_0(x)=\sum_{n=0}^{K}\frac{1}{n!}x^n$
- $f_i(x)=\sum_{n=0}^{\infty}\frac{1}{n!}x^n=e^x$
よって少し整理すれば,答は $N![x^N]f_0(x)e^{mx}$ です.
$e^{mx}=\sum_n\frac{m^n}{n!}x^n$ から,答を $\mathrm{polynomial}(m)$ の形で表せます.あとは多点評価を使えば,$O(m\log^2 m+n\log n)$ 時間で解けます.
Q – サイコロ
計算すべきは次の値です.
$$\mathrm{ANS}[k]=\frac{1}{NM}\sum_{i,j}(A_i+B_j)^k$$
素直に二項定理で展開すると,
$$\mathrm{ANS}[k]=\frac{1}{NM}\sum_{d=0}^k\binom{k}{d}\sum_{i}A_i^d\sum_{j}B_j^{k-d}$$
となります.そこで $a_d = \sum_{i}A_i^d$, $b_d=\sum_jB_j^d$ とすれば,
$$\mathrm{ANS}[k]=\frac{1}{NM}\sum_{d=0}^k\binom{k}{d}a_db_{k-d}$$
です.よって $a_0,\ldots,a_K$ と $b_0,\ldots,b_K$ が求まれば,答は適当な畳み込みで求まります.
$a_d$ を列挙するには,次を使えばよいです:$\sum_da_dx^d=\sum_i\frac{1}{1-A_ix}$.
この有理式を分母分子の多項式の組として計算します.これは分割統治で $O(N\log^2N)$ 時間でできます.そのあとで係数列を求めればよいです.
R – ランダムウォーク
$n=2^N$ とします.
端での遷移確率が違うようにも見えますが,次の絵を見ると解決です.
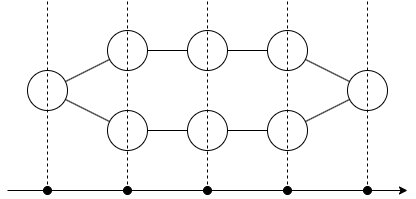
次のように考えることができます.
- 円環上をランダムウォークする(隣接する点は必ず $2$ 個あり,等確率に選んで進む).
- $x$ 座標だけを観測する.
円環上の頂点に適当に番号をつけると,(端だろうがなんだろうが)常に確率 $1/2$ ずつで番号が増減します.ただし番号は $\pmod{2n}$ で考えることになります.
結局,$(x+x^{-1})^{T}\pmod{1-x^{2n}}$ が求まれば ok です.これは繰り返し二乗法で求めると $O(n\log n\log T)$ といった計算量になりそうですが,今回は $n=2^N$ の制約からもっと簡単です.
FFT は巡回畳み込みの関係を各点積に変えるのでしたから,今回のような巡回畳み込みに関する $T$ 乗計算は,周期 $2^{N+1}$ の FFT をしたあと,各点で $T$ 乗をとり,IFFT で戻せばよいです.
知名度は多項式乗算よりも低いですが,むしろ通常は多項式乗算を,FFT と巡回畳み込みの関係を使って導出するという形で理解するはずなので,多項式乗算と FFT の関係を理解していればこれも理解できると思います.
S – ゲーム
type 1
問題 O のように EGF を作りますが,勝者に応じて $F_0(x), F_1(x)$ のように $2$ 種を用意します.
- $F_0(x)+F_1(x)=\sum_n\frac{n^{n-1}}{n!}x^n$ (ラベル付き根付き木の総数)
- $F_0(x)=x\exp F_1(x)$
これを求めるには,次ができればよいです:
- $n=0,1,2,\ldots$ についてオンラインに,$[x^n]F_1(x)$ を入力し,$[x^n]\exp F_1(x)$ を受け取る.
オンライン exp ということになりますが,$F=\exp f$ のとき $F’=f’F$ であることを利用すると,オンライン畳み込みに帰着できます.計算量 $O(N\log^2N)$ 時間で解けます.
なお,Newton 法で $O(N\log N)$ 時間にもなるようです.
type 2
気づかずに実験を書いてしまいましたが,このゲームは(一般グラフ上でも解けてしまう)有名なゲームです.
結局,完全マッチングが存在するような木を数えることになります.
これで,判定問題が bottom up な木 dp で解けるようになるため,これを同じように EGF で表せばよいです.ただし,私はこのことに気づく前に実験と OEIS で解いてしまいました.しかも欲しい実験結果はサンプルに全部ある.
T – カラフル
条件を満たす列は,次を順に並べることで得られます.
- 地点 $1$
- その他色の長さ正の頂点列
- (色 1 の頂点,その他色の長さ正の頂点列の結合)を非負整数回繰り返したもの
- 最後に地点 $1$
$A_1=998244353$ に備えて,少し冗長な表し方をしています(1, 3 番目だけを書いて最後に $A_i$ で割る,ということができない).
「その他色の長さ正の頂点列」の母関数を $F(x)$ として,答は
$$[x^{T-1}]F(x)\cdot \sum_{m=0}^{\infty}(A_1x\cdot F(x))^m = \frac{F(x)}{1-A_1xF(x)}$$
のように表されます.
結論は,$F(x)$ が $O(N)$ 次の有理式で,よって答の母関数もそう(答は $O(N\log N\log T)$ 時間で求まる)というものです.$F(x)$ を求めましょう.
包除原理を使います.つまり,いくつかの移動について「同色に移動します」という印を $-1$ 重みでつけて列を数えます.
印でつながった頂点をまとめて扱うと,結局次のようになります.
- 長さ $N$ の「その他色の長さ正の頂点列」を数えるには
- $N=n_1+n_2+\cdots+n_m$ と正整数に分割し
- それぞれのブロック内で,同色の移動だけからなる頂点列を作り,移動回数分だけ $-1$ の重みをつける
このブロックの母関数は,色ごとに考えることで $\sum_{i} (A_ix-A_ix^2+A_ix^3-A_ix^4\pm\cdots)$ という交代和の和になります.これは有理式の和なので有理式です.
U – 録画機
まず判定については,どの瞬間においても $2$ 台以下ということになります.
$A,B$ の作り方については,
- 多重集合 $A$ を決める
- 多重集合 $B$ を決める
- $A,B$ をマッチングする
というように考えます.時刻の昇順に数えていきます.
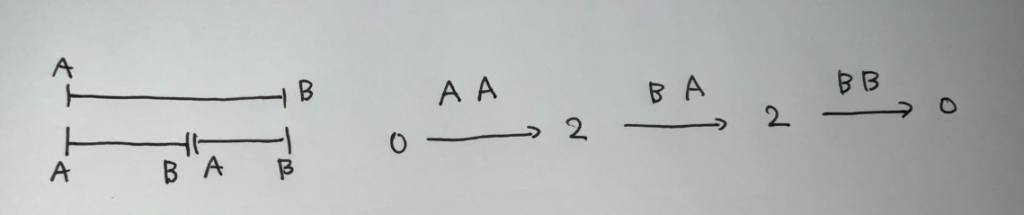
- $A$ を置くときには,ラベル(クエリインデックス)はつけない.最後に多項係数をつけることでラベルを確定させる.
- $B$ を置くときに,どの $A$ とマッチングさせるかを決める.
という要領で式を作ります.$2$ 台以下という条件については,カッコ列の累積和のような折れ線グラフを考えて常に高さが $[0,2]$ 内という形で処理できます.最後の多項係数をつける代わりに,多項係数の分母部分については $A$ を同じ座標に置く個数に応じてつけおき,最後に答に階乗をかけます.
これらを丁寧にやると,問題は次のように言い換えられます.
- $2$ 次以下の多項式からなる $(3,3)$ 行列 $F$ が与えられる.[$x^N]F^t$ を $t=1,2,3,\ldots,U$ で求めよ.
$F$ が行列ですが,ただの多項式のときとほとんど扱いは変わりません.分割統治で $O((N+U)\log ^2 (N+U))$ 時間で計算できます.
$O(N+U)$ 時間に高速化できる情報については,noshi91 さんのユーザー解説も確認してください.
V – 12 方向
まず,次の $2$ 種に分離して考えられます.
- 偶数方向,つまり $i=0,2,4,6,8,10$ の移動だけで見て $(H,0)$ に到達する.
- 奇数方向,つまり $i=1,3,5,7,9,11$ の移動だけで見て $(0,W)$ に到達する.
これは円分体論の知識があれば $\mathbb{Q}(\zeta_{3})\subsetneq \mathbb{Q}(\zeta_{12})$ であることからすぐに分かります.また高校数学レベルでも,軸ごとに見れば比較的簡単に証明できます.($x$ 方向に見ると $1, \sqrt{3}$ の有理数倍の移動しか起こらず, $H$ に到達するには $\sqrt{3}$ 由来の移動がすべて打ち消す必要がある).
よって次が解ければ十分です:偶数方向移動だけを使って,$n$ 回で $(H,0)$ に到達する方法の数え上げを $n=0,1,\ldots,N$ で求める.
適当な斜交座標を使うことで,次に帰着できます:$[x^H](x+y+xy+x^{-1}+y^{-1}+x^{-1}y^{-1})^n$ を $n=0,1,\ldots,N$ で求める.この状況は,問題 H と少し似ています.
$F(x,y)=x+y+xy+x^{-1}+y^{-1}+x^{-1}y^{-1}$ とします.これよりも
$$G(x,y)=2+F(x,y)=(x^{1/2}+x^{-1/2})(y^{1/2}+y^{-1/2})((xy)^{1/2}+(xy)^{-1/2})$$
の方が扱いやすいです.まず $[x^H]G(x,y)^n$ を列挙してからそれを利用して $[x^H]F(x,y)^n$ を列挙するというプランが立ちます.$[x^H]G(x,y)^n$ の列挙は,因数分解の形と二項定理から,「適当な二項係数 $3$ つの積を,適当な $1$ 次式の規則のところに沿ってたくさん足してください」というタイプの計算になり,式を書くと畳み込みで求められることが分かります.
以上をまとめると本問題は $O(N\log N)$ 時間で解けると分かります.
W – 閉路
これは FPS というよりも SPS (集合べき級数)が登場です.
二重連結部分グラフの数え上げを知っていれば新しい要素はほとんどありません.
- $G[S]$:頂点集合を $S$ とする部分グラフの個数
- $C[S]$:頂点集合を $S$ とする連結グラフの個数
- $B[S]$:頂点集合を $S$ とする二重連結グラフの個数
としたとき,$G = \exp C$ です.本問では $G$ がすぐに分かるので,そこから $C$ が分かります.
$C$ から $B$ を求めるには,次のような手順を踏みます.
- $F_0[S]$:頂点集合を $S$ とする連結グラフの個数
- $F_1[S]$:頂点集合を $S$ とする連結グラフであって,$0$ は関節点ではないものの個数
- $F_2[S]$:頂点集合を $S$ とする連結グラフであって,$0, 1$ は関節点ではないものの個数
- $F_3[S]$:頂点集合を $S$ とする連結グラフであって,$0, 1, 2$ は関節点ではないものの個数
- $\vdots$
$F_r$ から $F_{r+1}$ を求めるところができればよいですが,これは $F_{r+1}$ から $F_r$ を求める手順を考えた方が分かりやすいと思います.値の変更を行うのは $r$ を含むところのみで,$r$ 以外に共通頂点を含まないような部分グラフをマージするというタイプの計算をすることになります.この計算は,SPS の $\exp$ であることが分かります.
逆に,$F_r$ から $F_{r+1}$ を得るには SPS の $\log$ をとればよいことが分かります.よって $B[S]=F_N[S]$ は,$N$ 回の SPS $\log$ によって $O(N^3\cdot 2^N)$ 時間で計算できます.
一方で,これを逆にたどれば,$B \to C\to G$ 順に計算することもできます.これをそのままやっても元に戻るだけで意味がありませんが,
- $B'[S]$:頂点集合を $S$ とする二重連結グラフの個数,ただし頂点 $0,N-1$ は頂点数が $3$ 以上の同じ二重連結成分に属することはない.
- $C'[S]$:頂点集合を $S$ とする連結グラフの個数,ただし頂点 $0,N-1$ は頂点数が $3$ 以上の同じ二重連結成分に属することはない.
- $G'[S]$:頂点集合を $S$ とする部分グラフの個数,ただし頂点 $0,N-1$ は頂点数が $3$ 以上の同じ二重連結成分に属することはない.
のように修正して同じ計算手順をたどれば ok です.$B$ から一部の値だけを $0$ に修正することで $B’$ が得られ,そこから $B’\to C’\to G’$ と計算していけば答(を全体から引いたもの)が得られます.
X – 関数的平方根
hos さんの提出からびっくり解法.
$F(x)\in \mathbb{F}_p(x)$ の $k$ 回合成を $F^{(k)}(x)$ と書くことにします.このとき,$F^{(p)}(x)=x\pmod{x^p}$ が成り立ちます.
このことを確かめましょう.$V$ を $p$ 次未満の多項式全体として,$\phi\colon V\longrightarrow V$ を $g(x)\longmapsto g(F(x))$ とします.このとき,$\phi$ を基底 $1,x,\ldots,x^{p-1}$ で成分表示すると,対角成分を $1$ とする上三角行列になります.よって $(\phi-\id_{V})^p=0$ となり,$\id_{V}$ と $\phi$ の可換性および,二項定理から $\phi^p=\id_{V}$ となります.
ここから,$F(x)=G^{(2)}(x)\pmod {x^p} \iff F^{((p+1)/2)}(x)=G(x) \pmod{p}$ という同値が,$\implies$ も $\impliedby$ もどちらも容易に示せます.
結局答を求めるには入力の $F$ を $(p+1)/2$ 回合成すればよく,$O(N\log^2N\log p)$ 時間で解けます.

