A. Mainak and Array
両端が初期状態から変化するかどうかで場合分けします.
B. Mainak and Interesting Sequence
最大値以外は偶数個.というのが条件です.
$N$ が偶数のときには,すべて偶数回登場ということになります.$M$ が偶数であること,$N\leq M$ が必要で,それらが満たされていれば構成できます.
$N$ が奇数のときには,$1, 1, 1, \ldots, 1, x$ の形を考えればよいです.
C. Jatayu’s Balanced Bracket Sequence
累積和の折れ線グラフを考えて,辺が張られるとしたら同じ高さの点同士です.
高さが小さいところが挟まったところで成分が分割されます.
D. Edge Split
同色の辺でサイクルができないようにできれば最小化達成です(一本足すごとに成分が減らせている).全域木をひとつとって,残った辺が森になっていれば成功です.
制約より「残った辺」は $3$ 本以下なので,これが失敗するのはこの $3$ 本が三角形になったときだけです.作った全域木を $T$ として,この $3$ つの辺を $a,b,c$ としたとき,$T$ を $T+a-d$ の形の全域木に取り換えるということをします.$b,c$ と合わせて三角形になるような辺は $a$ 以外にはないので,これで上手くいきます.
E. Almost Perfect
辺 $i\to p_i$ によりサイクル分解します.
サイクルの長さは $1,2,4$ のどれかです.これはサイクル上の点を $a[0], a[1], a[2],\ldots$ として,列 $a[0], a[2], a[4], a[6],\ldots$ を考えると分かります.結局成分ごとに
- 長さ $1$ のサイクル.
- 長さ $2$ のサイクル.
- 長さ $4$ のサイクル.$x,y,x+1,y+1$ や $x,y+1,x+1,y$ の形になっている.
のどれかというのが条件になります.
まずタイプ $4$ の $(x,x+1)$ を $2$ 人組として,$2$ 人組 $2k$ 個とその他の人材 $n-4k$ 個に分割します.これは列を長さ $1,2$ の区間に分割する方法を考えればよくて,単に二項係数です.
この二項係数に,「$2$ 人組 $2k$ 個から $k$ 個の長さ $4$ のサイクルに分割する方法」「$n-4k$ 人を長さ $1,2$ のサイクルに分割する方法」の個数をかけて足し合わせればよいです.それぞれ $n$ 人目の組み方を決める dp で前計算しておけます.
G. A Certain Magical Party
最初に全員が同じ値のときは自明.最小値の人に注目します.このような人は $1$ 人だけである必要があり,操作順によらず最終的な値 $X$ が確定します.$X$ より初期値が大きい人が居たら矛盾.
$A$ が大きい人の操作状況は $A$ が小さい人には影響しません.このことから,$A$ が小さい人だけに限定した操作順に大きい人を挿入していくタイプの数え上げを考えます.
ある初期値の人を挿入することを考えます.初期値が $X$ 未満であるとします.
このとき,挿入するタイミングによって小さい・大きい happiness の人数は完全に決まるため,挿入すべき位置が完全に決まります.妥当な挿入すべき位置が存在しないなら答は $0$ になります.$B[i]=0$ の人は同じ場所に挿入することになり,ここに階乗の自由度が発生します.
初期値が $X$ の人もだいたい同じように計算できます.
H. Mainak and the Bleeding Polygon
確かに難易度は高いですが,基本的にはやるだけ計算問題です.
(短い辺の長さが $1$ の長方形の場合を除き)次を求めればよいです.
- $1$ 頂点に隣接する $2$ 辺によってつくられる領域の面積
- そのような連続する $2$ つの領域の交わりの大きさ
まず領域境界となる包絡線のパラメータ表示を求めます.(ここが一番難しいと思いますが,公式解説では全ての計算が省略されて答えだけが書いてあってすごい).私は次のような斜交座標を使いました.
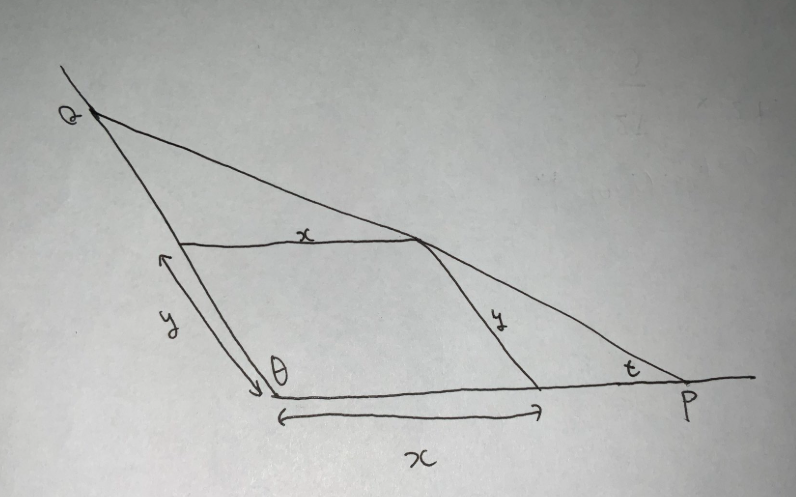
$PQ$ の長さは正弦定理で求めると
$$PQ=\sin(\theta)\left(\frac{x}{\sin(\theta+t)}+\frac{y}{\sin(t)}\right)$$
となります.$(x,y)$ が領域境界上にあることは,$t$ を動かしたときの $PQ$ の最小値の長さが $1$ であることです.長さを $t$ の関数と見て微分して,$0$ となる $t$ のところが問題です.ここから
$$x\sin^2(t)\cos(\theta+t)+y\sin^2(\theta+t)\cos(t)=0$$
が分かります.ここから $x=a\sin^2(\theta+t)\cos(t), y=-a\sin^2(t)\cos(\theta+t)$ と書けるので,これを $PQ=1$ に代入すると $a=\frac{1}{\sin(\theta)}$ となり,
$$x=\frac{\sin^2(\theta+t)\cos(t)}{\sin(\theta)},\qquad y=\frac{-\sin^2(t)\cos(\theta+t)}{\sin(\theta)}$$
が得られます.これが $(x,y)$ のパラメータ表示です.あとは $x(t)y'(t)-x'(t)y(t)$ を積分すればよいです.ここは私は Sympy(Python) に任せました.提出ソースコード(C++)に結果は残しています.
パラメータ表示を得る過程で,$(x,y)$ が領域内に含まれるかどうかの判定関数を実装することもできます.$(x,y)$ に対する $t$ を求めるには $x\sin^2(t)\cos(\theta+t)+y\sin^2(\theta+t)\cos(t)=0$ を解けばよいですが,ここは二分探索を使って数値的に求めます.
すると,$2$ つの領域の交わりは例えば数値積分を使って求められます($x$ に対して最大の $y$ を求めるなど.上の計算は斜交座標を使っていたので,$2$ 領域に共通の直交座標との座標変換を通しています).
交点の位置だけ求めてしまえばあとはそれぞれの曲線に対する積分に分かれるので,数値計算をなくすこともできます.

