A. Planning
手前から順に,その時刻までに配置できるもののうち最も遅延コストが大きいものを置いていく貪欲でできます.
B. Jury Meeting
「$i$ 日目までに全員到達するためのコスト」「$i$ 日目以降に全員期間するためのコスト」をそれぞれ独立に計算しておけばよいです.
C. Boredom
余事象を数えます.左側・右側・上側・下側に収まってしまう場合を引きます.包除原理を考えれば,$8$ つの長方形領域に対して点を数えればよいことになります.
D. Michael and Charging Stations
ポイントを大量に保有するパターンは考えなくてよいです.あるタイミングでのポイント使用をより早いタイミングでのポイント使用に変更する議論を考えればよいです.
よって所持ポイント量をキーとして dp で計算できます.
E. Lada Malina
まず移動範囲は適当な凸 $2k$ 角形です(線分 $k$ 個の minkowski 和).これを $X$ とします.
「$p_i-f_j \in t_i X$ のときに $ANS[i]$ に $a_i$ を足してください」という問題になります.
凸多角形の補集合は,$2$ つの半平面の交わり(斜交座標に関する第一象限のようなもの)の和で表せます.
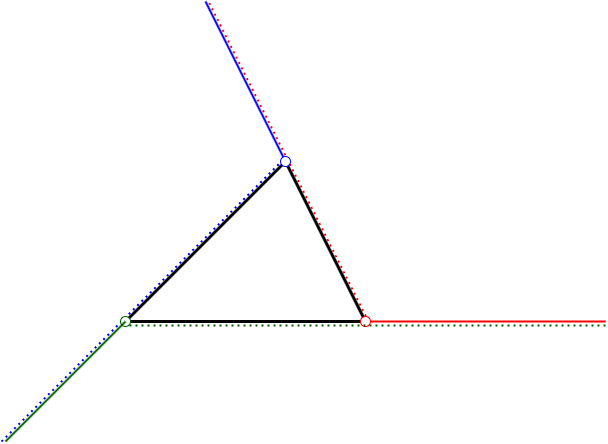
よって,そのような領域の場合の計算 $2k$ 回で解くことができます.式を整理すれば,静的な重み付き点集合の長方形和をとるクエリに帰着できることが分かります.

