概要
私はすぐに解けたやつです。というか、実は作問ストックに置いていた問題とほぼ完全に一致していました。数学知識なくても、それほど厳しくはないと思うのですが、あまり解かれてはいないですね。
$\Z[i] = \{x+yi\mid x,y\in \Z\}\subset \C$ を Gauss 整数環(その元を Gauss 整数)といいます.
問題の言い換え
複素平面で考えます.平行移動して、$0$ を通るとしてよいです.
格子 $\Z[i] = \{x+yi\mid x,y\in \Z\}$ の回転・拡大は,複素数倍で表せるので,おおよそ次の問題です:
Gauss 整数の集合 $x_1,\ldots,x_n$ が与えられる.任意の $i$ について $x_i \in d \Z[i]$ となるような複素数 $d$ がどのようなものかを考察せよ.
$x_i\in d \Z[i]$ と書きましたが,これは Gauss 整数環における整除関係 $d \mid x_i$ と同値です.(環 $A$ において $a\mid b\stackrel{\text{def}}{\iff} \exists c \in A, b = ac$).
Gauss 整数の集合 $x_1,\ldots,x_n$ が与えられる.これらの公約数 $d$ がどのようなものかを考察せよ.
最大公約数の問題っぽいですよね.正当化していきます.
Gauss 整数環の性質(Euclid 整域)
Gauss 整数環 $\Z[i]$ は性質が良く,公約数の計算,「素因数分解」の理論など,$\Z$ の整数論の類似が成り立ちます.
その根拠となるのが,$\Z$ と同じように「余り付き割り算」ができるという性質です(一般に Euclid 整域 と呼ばれる性質です).
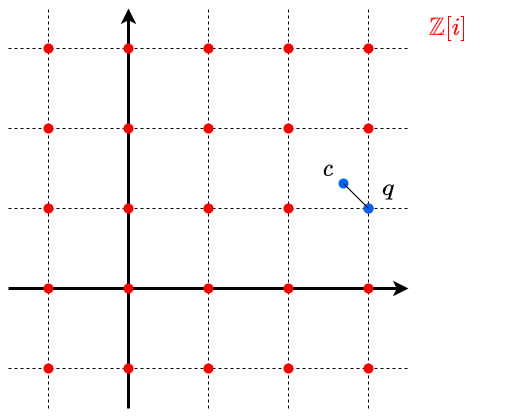
【命題】$a, b \in \Z[i]$, $b\neq 0$ とするとき,$q, r\in \Z[i]$ であって $$a=bq+r,\quad |b|>|r|$$ となるものが存在する.
【証明】$\C$ における商 $c = \frac{a}{b}\in \C$ を考える.これと $\C$ の距離について最も近い $\Z[i]$ の元を $q$ とおく.$r = a – bq$ とおく.これらが満たすことを確かめる.$$|r| = |a-bq| = |bc-bq| = |b|\cdot |c-q| \leq \frac{1}{\sqrt{2}} |b|$$ よりよい.
余り付き割り算ができるので,Euclid の互除法が行えます(Euclid 整域の名の由来です).
【定理】$(a,b)\in \Z[i]^2$ に対して,次のアルゴリズムは停止する:
$b\neq 0$ である限り、上の命題の $q,r$ をとり、$(a,b) \leftarrow (b,r)$ と取り換える.
停止した($b=0$ になった)ときの $a$ を $d = \gcd(a,b)$ と書くと,$d’\in \Z[i]$ に対して $$d’ \mid a\ \text{and} \ d’\mid b\iff d’\mid d$$ が成り立つ.
$\Z$ の場合の証明を思い出せば全く同様だと思いますが,一応概要だけ確認しておきましょう.
【証明】余りの性質により $|b|$ が減少量になる.$|b|^2\in \Z_{\geq 0}$ であるから減少は有限回で終わり,いずれ $b=0$ になって終了する.出力される $d$ について, 次が確かめられる:
- $d\mid a$ かつ $d\mid b$.
- $d$ は $ax+by$ (ただし $x, y \in \Z[i]$)と書ける.
ひとつめの性質から,$d’\mid d\implies d’\mid a, d’\mid b$ が分かる.ふたつめの性質から $d’\mid a, d’\mid b\implies d’ \mid d$ が分かる.以上により示された.
もとの問題
Gauss 整数の集合 $x_1,\ldots,x_n$ が与えられる.これらの公約数 $d$ がどのようなものかを考察せよ.
に戻ると,$d$ は「最大公約数 $\gcd(x_1,\ldots,x_n)$ の約数」であり,それは余り付き割り算を利用した $\Z[i]$ における Euclid の互除法で計算できることが分かります.最大公約数の場合が最大の $K$ になることも容易に分かりますが,省略します.
Euclid 整域
環 $\Z[i]$ (あるいは同様に,一般の Euclid 整域)において,公約数の理論が $\Z$ の場合と同様にできることを確認しました.
Euclid の互除法を基点として導かれる $\Z$ における理論はおおよそ一般の Euclid 整域に拡張できて,例えば次のようなことも成り立ちます(定義すらちゃんとはやりません).
- 既約元 $p$ は,$p\mid ab\implies p\mid a \ \text{or} \ p\mid b$ を満たす.
- 既約元分解の一意性が成り立つ.
また,他に代表的な Euclid 整域の例としては,体上の $1$ 変数多項式環 $K[T]$ があります.1変数多項式における「余り付き割り算」,高校数学で学びますよね,あれです.この性質から,既約多項式への因数分解の一意性なども $\Z$ における素因数分解の理論と同様に証明できるというわけです.
$\Z[i]$ は,「2 次体の整数環」と呼ばれるものの特殊ケースになっています.他には
- $d=-2$:$\{x+y\sqrt{-2}\mid x,y\in \Z\}$.
- $d=-3$:$\{x+y\frac{1+\sqrt{-3}}{2}\mid x,y\in \Z\}$.
なども Euclid 整域です.参考:https://oeis.org/A048981
一般の $2$ 次体の整数環においては,互除法ができないどころか,「最大公約数」の定義も不明確になります.例えば
$$d’ \mid a\ \text{and} \ d’\mid b\iff d’\mid d$$
となる $d$ は一般には存在しません.(代わりにイデアル論というのがあります,流石にこの記事でやる話ではなくなってきたのでおしまい).

