| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | |||
| 結果 | AC | AC | AC |
全体感想
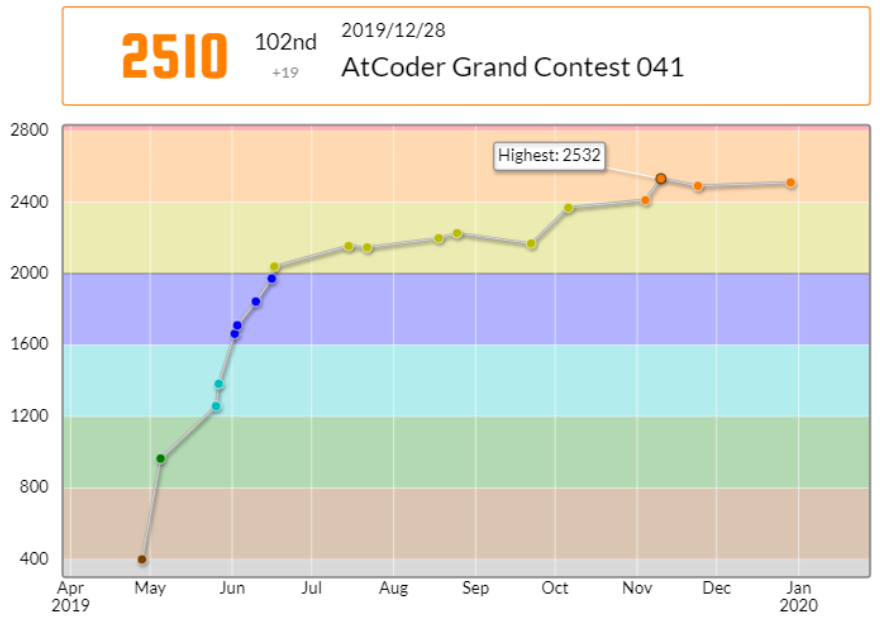
72分3完で、102位でした。
体感としてはやや失敗寄りくらい。なのですが、そう感じながら橙パフォが出ているのは実力向上と思って良いんでしょうかね?とはいえ反省材料のない回の方が稀なので、アテにならないですが…。
以前はあまり「前から解く」をやっていなかったのですが、最低水準も底上げしていきたいと思い、多人数解きそうな問題はさっさと解く意識でやりました。(全問20秒ずつくらい読む→とりあえず前から解く)。
Cまでで、3WA。加えて無駄なタイムロスも多かったです。とはいえ、最速3完でもパフォ150程度しか違ってこないため、スピードについては割と上手くいっていたようです。夏頃と比べて解く遅さを嘆く頻度は少なくなってきて、そこは良い感じかもしれません。
Dはそもそもめちゃ大事な初手で考察ミスしていたことがコンテスト後に発覚。これは解きたかった…。本番中はなかなか手がかりが見えず、Eと行ったり来たりしている間に残り数十分。
過去問でもD難易度はだいぶ埋まってきているので、もう少し自分と順位表を信じてDに専念した方が良かったかもしれません(結果論)。4完はまだ1度しか実現していないです。狙える確率は割と上がってきていると思うのですが…引き続き練習していきます。
問題B – Voting Judges
・ソートする
・「i 番目の問題が採用されうるか」という判定問題を解いて、二分探索する
という方針はすぐに立つと思います。問題ごとに、採用されるための最適戦略は変わりそうなので、狙いの問題を固定して考えたいというのは自然でしょうかね。
採用を目指す問題を決め打ってみます。何問かを追い抜かさなくてはいけないですが、追い抜かしやすいものを狙えばよいです。最終的に採用する問題セットを固定できます。
・1 2 3 4 5 5 6 6 6 7 (入力例3)
$M = 4$ 回の投票を行います。流石に目標とする問題には毎回入れるとしてよいです(そうでない採用プロセスがあったとして、反例となる投票を修正しても採用プロセスになる)。上位陣も投票する不利益はないので、毎回投票してよさそうです。
他の問題への投票、雑に被害の少なさそうな戦略を考えると、「各時点でスコアが小さいものを優先して」などとなりそうです。しかし、「各時点での戦略」という見方をしても、M回積み重ねるシミュレーションは無理ですし、考察の上でも、時系列でスコア順位がめまぐるしく変化するためややこしそうです。
そもそも1回目と2回目の投票先を入れ替えたりしても最終結果は変わりません。1手ずつ戦略を決めること自体が非本質で、M回の投票の総和で何が実現できるのか、何を実現したいのかという視点で考えます。
・実現したいこと → 問題ごとの、投票して良い上限回数を守りたい
・実現できること → ?
投票での変化量のみに注目します。
操作(★):$(0,0,\ldots,0,0)$ に対して「$V$ 箇所に $1$ を加える」を $M$ 回行う
でどのような数列が実現できるでしょうか?必要条件として、
条件(※):「全て $M$ 以下であること」「総和が $MV$ であること」
がすぐに思いつきます。これが逆に十分条件であることも証明できます。$M$ に関する帰納法で示します。$M = 0$ は自明。$M-1$ で成り立つとして $M$ の場合。「ちょうど $M$ を作らなければいけない場所」は $V$ 箇所以下です(総和の条件から)。そこを含むような $V$ 箇所を初手でとってあげれば、帰納法の仮定が適用できます。
ところでこの部分問題、本質的に次の問題とだいたい同じです。
★ABC 143-F:Distinct Numbers★
★[AtCoder 参加感想] 2019/10/19:ABC 143★
今回は、問題ごとの「上限回数」を与えての投票操作ですので、全て $M$ 以下の範囲に書き直したあと、総和が $MV$ 「以上」であることを確かめればよいです。また、「上位の問題は毎回投票するとしてよい」などの考察は通る方が自然かと思いますが、最終的にはこの区別はいらないです。
・1 2 3 4 5 5 6 6 6 7 , $V = 8$, $M = 4$
・上限回数:[4,4,3,2,1,4,4,4,4] → 総和 30 → $MV = 32$ 未満なので、この問題は採用できない。
ABCをちゃんと勉強していたおかげもあってか、考察はスムーズでしたが、 無意識のうちにバグ修正しちゃったせいで、正しいコードからバグを探して時間を溶かしました。あれれ、何やってんだ。
問題C – Domino Quality
結構、苦しんだという声を見ましたが、私は割と迷わずに解けました。30分2ペナはそれほど優れた成績ではないですが…。
「気づき」を論理立てて文章にするのは限界があるので、適当に考察ノートを貼ってみます。
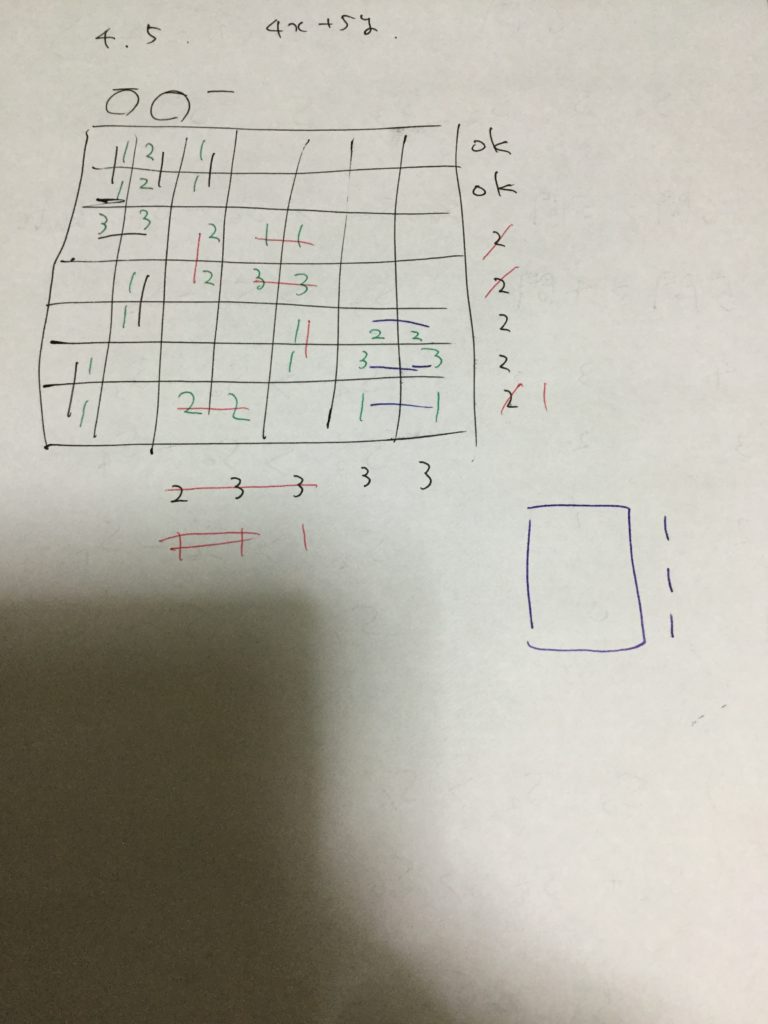
・目標クオリティを決めて、まずはかなり適当に、実際に並べてみます(手計算)。
・1枚置くごとに、目標値が修正されていきます。
・わりと一瞬で、「1枚置くと、クオリティの和が3変化する」ことに気づきます。
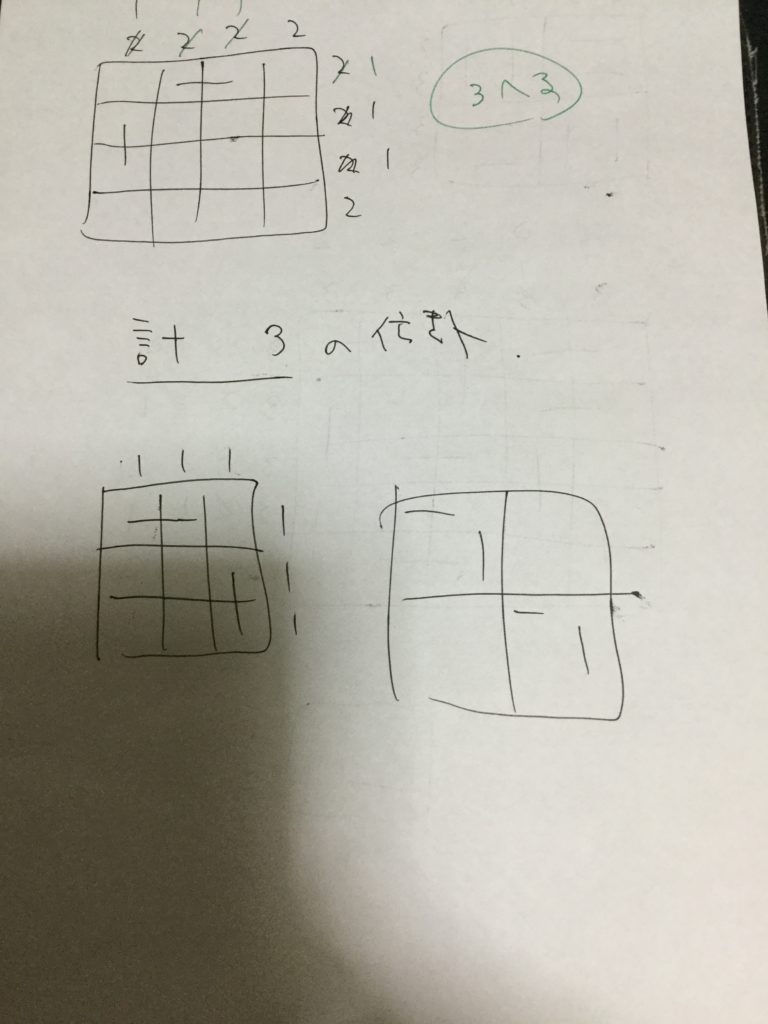
・スコアの合計が $3$ の倍数です。$3\times3$, $6\times 6$を作ります。$6$ の場合は、$3$ の場合をまず置いてみて残り部分を考えました。対角に並べるという発想は典型っぽいですが、ここで早めに気づけたのは少し運も良かったのかも。
・「3の倍数が必要」と唱えているうちにいつの間にか $N$ が3の倍数と誤考察。提出して1WA(ひどい)
・$N = 4$ を構成。クオリティ $3$ 目標なのは分かっているので、すぐに作れる。これは転置を除いて一意です。
・$N = 5$ を構成。適当に置いていきます。「一意に決まる」みたいな要素がほとんどなくて、不安ですが、逆にいうと条件はゆるゆるで、よほど極端な残し方をしなければ、ある程度大胆に行っても上手くいくっぽいです。
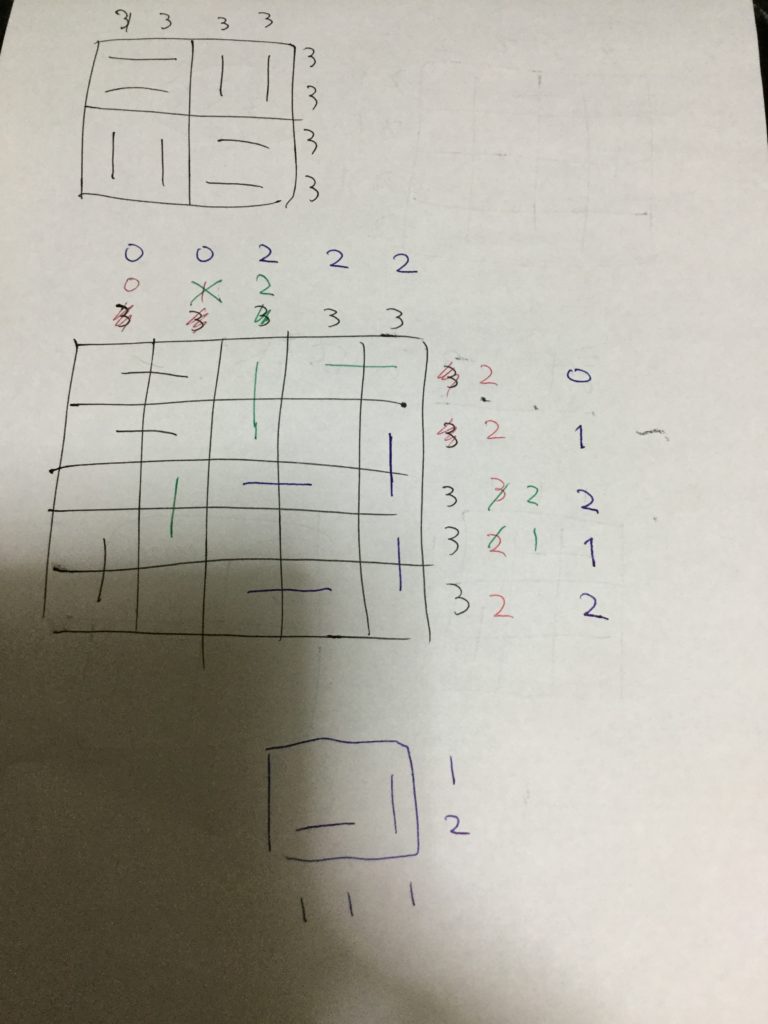
・対角のアイデアがあったので、$4x + 5y$ ができることを確認。残タスクを考えると、$N = 7,11$ がまだです。$N = 7$ ができると良さそうです。また適当に並べると作れます。「こういう置き方の方が、後で調整しやすいかな?」の類は結果的にはほとんど無駄で、どんどん大胆に行けばほとんど詰むことはなさそうです。クオリティ $3$ だと分かっている前提ではありますが。