[yukicoder]初めての作問（yukicoder contest 242）

2020.04.03

コンテストページ：■

参加してくださった方、ありがとうございました！
そうでない方も、お時間のございますときに、是非考えてみてください。
面白いと思った問題には、yukicoder の問題ページから Fav★ をしていってくれると嬉しいです。

競技プログラミングでの作問・出題は初めてでした。作問作業に関して経験したことや、個別の問題の出題にあたって考えたことをまとめます。テストケース作りの思考プロセスや、具体的な生成アルゴリズムなどは、表立って語られていることを、私はあまり見たことがありません。その辺についても、今回のことを書いてみました。

作問経験たった $5$ 問時点で書いているので、理解不足もかなりあるかと思います。また作った問題や、私のアプローチが外れ値側に寄っている可能性もありますので、ご了承ください。

特に今後作問してみたいと思っている方が参考にできる部分があればいいなと思いますし、そうでない方も適当に楽しんでくれると嬉しいです。

「問題別のはなし」は、解法のネタバレを含みます。

スポンサーリンク

参考文献

勉強に利用したものを貼ります。

いずれの記事も、大変参考になりました。ありがとうございます。

また、それでも不明な点などは、yuki さん（yukicoder 運営）、beet さん（tester）に相談しながら進めて、何とか形にすることができました。ありがとうございました。

全体的なこと

問題の原案

$12$ 月くらいからこまめに蓄積していたので、選びながらセットを組める程度の在庫はありました。

yukicoder には「セグメント木コンテスト」「木上クエリコン」のようなテーマ統一回という前例もありますが、今回は、ある程度分野がばらけるようにしました。数学セットを期待してくれていそうな方も見ましたが、今回はむしろ数学セットと言われないようにバランスを取っています。

D・E は割と硬派な競プロという感じで、青レート＋くらいはないと手がつかなかったと思います。その分、B・C は典型色が少なめで、慣れている人でも少し悩んだり、またレートが低い人でも十分チャンスがあるような問題になっているつもりです。

難易度評価は気持ち高めにつけています。yukicoder の同じ ★ の数のなかでは易しい側になると思います。（えええ…そうでもなかったですかね？）

問題文、解説の作成

MathJax（LaTeX）も経験があり、問題文の作成は競プロに限定しなければ経験がありますので、苦労は少なかったです。書いたものを結構細かいところまで指摘していただけたので、勉強になりました。

e869120 さんの記事 では、解説作成は作業工程の終盤に置かれていましたが、私はかなり早い段階（最序盤）で執筆しました。解法をきちんと文章化してみるというのは、問題・解法の正当性の確認のための強力な方法だと思います。あとから別解法を思いついて追加作業が生じたところもありましたが、ごくわずかでした。

想定解の準備

特に苦労はなかったです。AC か WA かを判定してくれるジャッジは存在しませんから、可能であれば、愚直解も実装して照合しながら進めると良いと思います。

テストケース作成

ここが本質？未経験分野ということもあり、作業時間の大部分を占めました。

問題ごとに後述しますが、思った以上にここも競技プログラミングでした。

課題を定式化して、解決するためのアルゴリズムを考えるという作業も必要になりました。 $1$ つの問題に対してアルゴリズムを複数実装したりしていると、問題を解く以上の思考量・実装量です。不慣れゆえ、問題傾向の偏りゆえという面もあるのかもしれません。

普段のコンテストでも、解く側から見えない苦労がいろいろあるのだろうなあ。何かあったときに 「テストケースに欠陥がある！」と騒ぐのは簡単ですが、たった $5$ 問をある程度体裁を整えるだけでもなかなか大変でした。

すこし神経質にやりすぎたということなのかもしれないですね。特に公的なコンテストでもないのであれば、私の準備よりは雑でも大丈夫なのかなと思います。

generator の実装

python の文法で generator というのがあるので、ややこしい…テストデータの生成についてです。初め、beetさんの公開しているサンプル にならって、生成アルゴリズム別にファイルを分けていたのですが、何度も出力用の関数を書いて無駄をしている気がしてきたり、ファイル名のインデックスの管理が手間になる気がしてきたので、途中から方針転換してひとつにまとめました。だいぶ人によるらしいです。

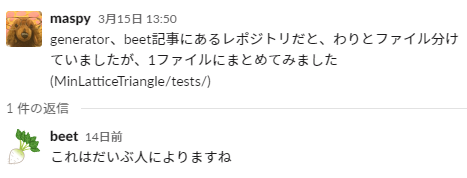
def write_all(gens):
    for i, g in enumerate(gens, 2):
        category_name = f'{i:02}_{g.__name__}'  # 02_small など
        for j, N in enumerate(g):
            write_case(category_name, j, N)

gens = [small(5), middle(5), large(10), hand()]
write_all(gens)

こんな感じで、generator 関数（これは python 文法）のリストを渡すことで全ケース書き出されるように実装して、あとは生成アルゴリズムを考える部分に専念しました。

なお yukicoder の問題文サンプルからテストケースが生成した場合、自動で 「01_sample_01.txt」のような命名がされるため、手元生成のものは 02 から順に大分類のインデックスを割り当てました（yukicoder では問題名の辞書順が実行順序に影響しますし、 意図したとおりに大分類番号をつけて並べる方が綺麗かと思います）。

コンテスト後の反省

yukicoderは、3か月ほど問題を解かせていただいていますが、金曜夜に居合わせられることが少なかったこともあり、コンテスト参加経験は少ないです。コンテスト仕様について十分理解していませんでしたが、コンテスト本番中にもテストケース名は読めるようです。ここについては自覚していませんでした。私の用意したテストケースでは、「small_yes」「small_no」のようにyes, noどちらのケースで落ちているかが判断できたり、「M_equal_1」「repeated」のように考察の主要な場合分けまわりが公開されたりしていました。ぐぬぬ、失敗です。この記事や私のソースコードなどを作問の参考にされる方は、注意してください（良くない側の例です）。

→ 2020/04/04 追記：

私のような作り方でも問題ないようになりました。

validator

業界標準が、testlib.h を利用するもののようだったので、C++ で実装しました。ちゃんとしたコンテストでは複数人が実装するのが慣例のようで、tester も独立に validator を実装してくれました。

普段は python で競技プログラミングをしていますが、特に問題にならなかったです。次に入力されるものに応じて 「inf.readSpace();」「inf.readEoln();」「inf.readLong();」等を書き並べるだけですので、C++ を触ったことがなくても習得難易度は低いと思います（私は C++ を触ったことがあります）。

その他

  • セットでの出題について

セット全体としてのバランス（難易度・分野）をコントロールできる利点があります。デメリットとして、作業量が多いです。平均しても、$1$ 問あたり $20$ 時間という単位で時間をかけたような気がします。はじめは気楽に「とりあえず $5$ 問くらい出題してみよう」と思っていたのですが、未経験者が気楽に挑む量ではなかったかもしれません。

  • writer ？ tester ？

主観になりますが、先に writer を経験したのは良かったと思っています。writer 目線で一通りの作業を経験させていただいたことで、今後 tester としても知恵を出しやすくなるのではないかと期待しています。募集があれば手を挙げるかもしれないですし、個人的に声をかけていただければ協力できると思います。（この記事を読んで、特に作業環境が近いと思った方であれば、より役に立てるかも）。

初手を tester として作問作業について学ぶ場合には、ある程度慣れている writer の下について、なんでも質問しながら教えてもらうのが良いのかなと思います。

作業環境など

つかったもの。

  • Windows 10 + WSL (Windows Subsystem for Linux）
  • Python3.8（想定解法コード、generator）
  • C++（validator）
  • GitHub（tester とのファイル共有）
  • Rime
  • slack（tester とのやりとり、yuki さんとのやりとり）

Rime

yukicoder での出題にそれを当てはめる必要はないのですが、一般的なコンテストの作成過程にも興味があったので、我流ではなくなるべく業界標準的な方法で作業を進めるように心がけました。

競技プログラミングの作問では、 Rime を使うのがある程度一般的な方法のようです。チュートリアルとして、Rimeの使い方（beetさん）にある通りにコマンドを写経したり、自分でも generator を書きなおして動作を確認したりしました。

rime_init --git
rime add . problem <dir_name>
rime add . solution <dir_name>
rime add . testset tests
rime test
rime pack

これだけ覚えれば、とりあえず使えると思います。簡単ですね。「rime_init」はプロジェクト作成時、「rime add」類もディレクトリ作成時に一度ずつ使用するだけです。頻繁にたたくのは、「rime test」だけです。カレントディレクトリに応じて、プロジェクト全体・問題ごとのテストが可能です。

GitHub レポジトリ

GitHub 作業レポジトリ（コンテスト後公開） → https://github.com/maspypy/create_yukicoder_problem

テストケース生成器（generator）やジャッジコードを全て python で実装しています。界隈では前例が少ないので、参考のためレポジトリを公開しておきます。

yukicoder

作問は、右上の自分の名前のところから行えます。一度問題を作成すると、以降は「問題一覧」から確認できます。問題名も後から変更できますし、勝手に出題されてしまうこともありません。特に不可逆な要素はありませんので、気楽にいろいろ試しちゃって大丈夫だと思います。

  • 問題文・解説はここから編集可能です。私は全てブラウザ作業で行いました。
  • テストケースの登録には、いくつかの方法があります。私が使ったのは、
    • 編集画面の「テストファイルを作成する」：問題文に含めたサンプルが、テストに自動追加されます。
    • テストのファイルアップロードから。Rime の出力フォルダに行って、CTRL+A などで選択することで、まとめてアップできます。私は Windows から WSL 環境にファイルを置いていましたが、エクスプローラー等でディレクトリ「\\wsl$」を指定するとアクセス可能です。
  • 他に、入力データと想定解から自動で出力データを生成したり、生成用のコードから入力データを生成する機能が、yukicoder 内に備わっているようです。今回は使用しませんでした。
  • 「管理」画面からあれこれできます。「リジャッジ」「テストケース削除」を主に利用することになりました。また、「テスターコード生成」（テスター依頼用）もここです。テストケース全削除がワンクリックでできることを把握しておきましょう。ある程度気楽に失敗できます。
  • 巻き戻せない要素としては、提出コードはお試しで投げたものがすべて残ると思います。くらいかな。特に困らないかと思います。

Slack

途中からですが、問題ごとにスレッドを立てました（初めからやっておいた方が良かったと思いました）。あとは適当です。

問題別のはなし

A：おつりは要らないです

適当な易しい枠のつもりで、割と典型に近い貪欲かと思います。貪欲解の正当性を検討する習慣がない人は、この機会に証明を考えてみてはいかがでしょうか。 ※ 反省：この問題の難易度が、最も、推測を外してしまったようです。 参加者目線だと $0$ 完と $1$ 完で受ける印象は結構違いますし、もうちょっと難易度の調整をすべきだったかぁ…。

考察を進める上での選択肢としては、「1000円札側から決めることを考える」「10000円札側から決めることを考える」「最安値から処理することを考える」「最高値から処理することを考える」あたりを思い浮かべて妥当性を検討していくと、解説通りの方法に行きつくと思います。

この問題がもっとも何も考えずに作ったのですが、テストケース作りは悩まされました。指定の制約下でランダムの数値を決めると、たいてい No になってしまいます。はじめは「各店で使用するお札の内訳を決める → ぎりぎり Yes / No になるように $A_i$ を決める」というので良いかなと思っていたのですが、この作り方だと（適当に端数を処理したあと）値段の合計を見るだけでもほとんどのケースで AC が出ます。また解説に挙げた「下から決める」解法は厄介で、最初に作ったデータセットでは $100$ ケース近くありながら AC が出ていたりしました。最終的に使用したアルゴリズムは以下の通り。

  • small_yes, no：$N\leqq 10$ と $A_i< 30000$ をランダムにとる。Yes になるまで、$X$, $Y$, $Z$ をランダムにインクリメントする。
  • large_yes, no：各店で使用するお札の内訳を決めたあと、ぎりぎりに値段設定。
  • anti_bottomup：解説に挙げたボトムアップ解の対策。これがまずいのはどういうときかを考察して、それに基づいて適当な構築アルゴリズムを実装します。$1000, 5000$ 円札が不足気味のときだけ。$1～3000$ 円に $1000$ 円札、$3000～5000$ 円に $5000$ 円札、$5000～10000$ 円の商品に $10000$ 円を当てる必要があるようなケースをランダムに作ったあと、全体的に $10000$ 円の倍数をランダムに加算しました。

B：三目並べ

AC をとっている人でも、証明（勝てない場合）をしていない方も多いかもしれません。証明も面白いので考えてみてください。

適当なゲームを考えたら、ちょうどひとつ非自明な勝利条件がある手軽な考察問題になりました。

クエリ化したのは、tester の提案です。実ははじめ、ほとんどの問題に対してテストケースが $100$ 個くらいありました。 易しめの問題で膨大な数のテストケースを用意すると、ジャッジが詰まる原因ともなるため、あまり良くない思考法のようでした。

yukicoder wiki
beet さん
e869120 さん

はじめは 「とりあえず各 Yes パターンに対して 10 ケースずつ！」とかやっていたんですよね。

クエリ化というのはなるほどです。多くの値を出力させることで、 1 つのデータセットだけであってもきわめて高い精度で、アルゴリズムの正しさを検証できます。出題形式について、そのような意図を考えたことはなかったです。なるほどなー。というわけで、適当にデータセット数を減らして完成させました。

本問題も、テストケース作り自体にアルゴリズム要素がありまして、ランダムに $3$ つの記号を並べていくだけでは大きな盤面はほぼ確実に「Yes」の答にしかならないです。また、問題設定の都合上つけくわわった、「o, x が同数ずつ」という制約も邪魔です。最終的には以下のようなアルゴリズム群を実装しました。

  • 盤面の末尾に ‘x’, ‘xoo’ を適切に追加して個数をそろえる関数を用意。気にせず作った盤面をこれによって修正して出題する。
  • small_yes, no：小さい盤面をランダム生成して、想定解プログラムで解く。期待する yes, no が出るまでまわして出力。
  • large_no：No となる盤面の ‘x’ から ‘x’ までの部分は、解説のように分類できる。密度パラメータを指定して、’x’ から ‘x’ までをそれっぽくランダム生成。盤面の長さが $900$ を超えるまで、それらをつなげる。
  • large_yes：まず、No となる盤面を作る。このうち適当な部分を繰り抜いて、yes となるように加工する。例えば長さ $7$ の部分文字列を ‘xo—ox’ に置きかえるといった具合。

C： Reiwa Sequence

タイトルが良い感じになって、11ヶ月前に出題できていたらさらにピッタリでしたが、何とか令和元年の出題です。「bit DPは / 半分全列挙は 制約で分かる」みたいな意見を見たことがありますが、いかがだったでしょうか。

※ これも、想定よりは解かれなかったです。上級者は、B よりも C の方が瞬殺かなーと思ったんですけど。制約が思ったより、強いめくらましになってしまったでしょうか。

作問ストックからではなく、セットを組み始めてから作問した問題です。他に作問に関して経験していないことはないかと考えていたときに、「スペシャルジャッジ問題」をひとつ出題しようと心に決めて作問しました（リアクティブ問題まで手を広げるとキャパシティーオーバーしそうだったので、それはやめました）。

ジャッジコードは python で実装しており、これは探した範囲では前例が見当たらなかったので、どなたかの役に立つかもしれません。前例が見当たらないこと、手元環境（rime）と yukicoder 環境でデータの受け取り方が異なるところなどで、少し苦労がありました。

ジャッジコード → https://yukicoder.me/problems/no/1017/code

また、数回「J_TLE」を観測しました（Judge TLE）。ジャッジコード自体の問題ではなさそうですので、ひとまず yuki さんに調査を委ねています。頻度は小さいことから、yuki さんと相談の上、今回のコンテストでは「J_TLE が出ているのを見かけたら個別にリジャッジする」という方針にしました。コンテストのクオリティについていうならばここは私の妥協判断です。ご迷惑をお掛けした方がいらっしゃいましたら、申し訳ございません。→ 大丈夫だった！！

解法まわり。現象としては「十分量探索すると必ず見つかる」みたいなところですので、適当な方法で 1.9秒間探して、なければ「No」を出力するような解法でもわりと通ってしまうかもしれません。一応、$20$ 項まで見ないと Yes にならないもの、$19$ 項の数列で唯一解のものなどは入っていて、$N3^N$ は落ちると思っており、$3^N$ の探索もかなり上手にやらないと落ちることを期待しています。$N2^N$ は通るのは想定通りです。

テストケース作りです。またもやアルゴリズム要素を求められます。ランダム生成だと、長さ $15$ 以上の「No」のケースがめったに生成できません。結局以下のようなものを実装しました。

  • 長さ 5 以下の Yes ケースを適当に生成：$n-1$ 個ランダムに決めたあと残りを Yes になるように埋める。
  • 長さ 10 ～ 25 の Yes ケースの生成：ランダムに作って解があるか確認
  • 長さ 11 ～ 14 の No ケースの生成：ランダムに作って解があるか確認
  • 長さ 19 の No ケースの生成：$19-n$ 項の Conway-Guy sequence 構成（解説参照）を $2^n$ 倍したあと、各 $0\leqq i < n$ に対して「$2^i\times 奇数$」をランダムに追加します。$2$ で割れる回数が少ないものから順に「$\pm 1$ 倍で使うとダメ」が証明できて、No のケースの完成です。
  • 長さ 19 の 唯一解 Yes ケースの生成： 例えば長さ $17$ の Conway-Guy sequence 構成を$4$ 倍し、適当な奇数 $x$ を $2$ 個加えると、「$x, -x$」の作り方で唯一解です。また、長さ $16$ のConway-Guy sequence 構成 を $7$ 倍し、$a\equiv2 \pmod{7}, b\equiv4\pmod{7}, c\equiv 6\pmod{6}$ となる $a,b,c$ を追加すると、「$a,b,-c$」の作り方で唯一解です。こういう感じの手段でいくつか作りました。似た方法で唯一解とは限らないけどある程度少なさそうなものも生成しています。
  • 巨大な部分和を経由する $19$ 項 Yes ケース：長さ $12$ の Conway-Guy sequence 構成を $127$ 倍したあと、 $\pmod{127}$ で $1,2,4,8,16,32,64$ の数を付け加える。追加した $7$ 元は全て 同符号で使う以外になく、これらを $150000$ 上限に近くとっておくことで、左右からの累積和が $10$ 万を超えないと解が構築できなくなります。解説で説明した通り、解く前にシャッフルすれば回避されます。

適当なスペシャルジャッジ作成を経験したかっただけなのに、これもテストケース作り難しいじゃないですか！

D：suffixsuffixsuffix

文字列の考察に慣れてきた頃に、自己研鑽のために考えた問題です。結構単純な結論になりましたし、前処理パートがなければボツにしていた気がします。ここがあるだけでも雑なサンプル合わせだけでは解きにくく、正しい考察の積み重ねを評価しやすくなったと思っています。

考察の中身は割と典型寄りかと思います。ただ、文字列の順序について有意義な考察をさせる問題は、AtCoderでも 黄～橙 難易度くらいにならないとほとんど例がないので、その辺の難易度の問題を数多く考えたり解説をじっくり検証したことがないと、解きづらかったかもしれません。

サンプル３が、1 周目と 2 周目で順序の入れ替わる本質的な例で、ここを考察の起点にしてもらえていると想定通りです。非自明な周期がある場合の発見についてはサンプルではなく、考察で辿り着くか、’aaa’ * 100 のような例を想起して疑問を抱くことを期待していました。

テストケース作りのコーナーです。うしろ２問は簡単。

でも実はこの問題もはじめ $100$ ケースありましたｗ「まずは小さい場合をですねー。文字の種類数を [1,2,3,5,10,26] にして… $M = 1,2,3,4,5$ でしょ。はい、$30$ 個つくれました。」みたいな感じでしたね。まぁ、流石にこれは簡単に減らせました。

作業手順に非自明なところがあるとすれば、まず愚直解を実装しておいて、照らし合わせながら想定解の検証とテストケース作りを進めました。

  • 愚直解１：超愚直。
  • 愚直解２：suffix array の構築以外は愚直。

これのために、小さな文字列の場合や、繰り返し回数の小さなテストケースも、ある程度の数生成しています。

愚直解のテストには、TLEすることはあってもWAは出ないことを要求します。このことを Rime 環境で実現するには、SOLUTION ファイルに、以下のように記述します。

script_solution(src='main.py', challenge_cases=[]) # shebang line is required

expected_verdicts([TLE, AC, RE])

TLE, AC, RE 以外が出たらエラーを出すようになります。この方法は matsu7874 さんの記事 で学ばせていただきました（RE を入れている理由：愚直解では文字列を $M$ 倍するところで、巨大な $M$ のときに RE するため）。

なお、全ケース AC にはならないことだけをテストするならば、単に「challenge_cases=[]」を含めればよいです。エラーメッセージを見て想定通りかを判断するのではなく、どのようにテストしたいかを設定して、想定通りに動いた場合にはエラーが出ないようにしましょう（反省）。

気になったことは何でも質問です。界隈に伝わる文字列ケース生成のひでんマシン、みたいなのはなさそうでした。

E：最小格子三角形

登場人物名は、「こうし」のアナグラムです。「Lattice」からとって、latti さん、latte さんなどという案もありました。なお、実在の人物とは一切関係がありません。

原案は全然違う格子点幾何だったのですが、それを考えているうちに、最小格子三角形がどのくらいあるのか気になりました。長い辺ごとに分類すると簡単な構造をしているの、知らなかったです。綺麗でびっくりしました。

余談ですが、正方形領域：$|x|, |y|\leqq N$, $N\leqq 10^9$ というような制約でも解けます。同じくらいの長方形領域でも解けます。よければ考えてみてください。だいたい これ です。出題者が面白いと思った考察パートよりも、類題経験の有無の方が大きくなりそうだったので、円での出題を選択しました。

本問も、愚直解法を $2$ つ作成してから作業しました。テストケース作成等、作問作業としては最も自明な癒しパートでした。

あとは、OEIS で簡単には解けないことを、OEIS素人なりにですが確認しました。

スポンサーリンク
タイトルとURLをコピーしました