| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
今回はわりとひどい出来(笑)
本質的に誤った解法をとってしまった問題はありませんでしたが、無限にTLEを食らいました。
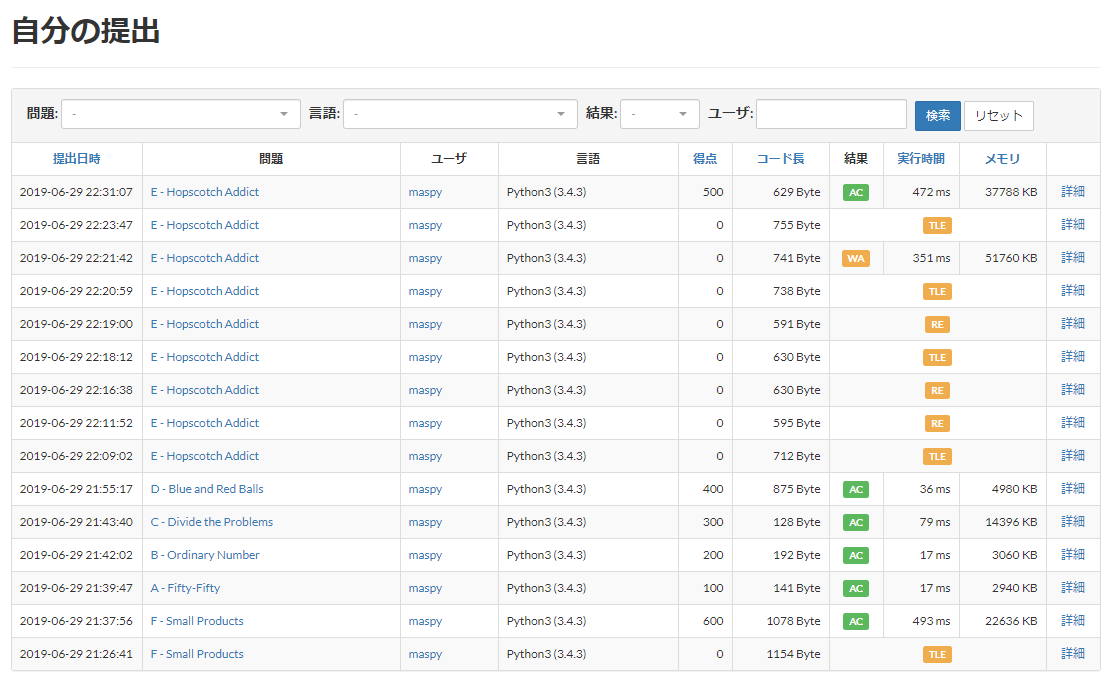
自分はrated対象外なのをいいことに、提出デバッグですw
全問正解難易度もそれほど高くないので、ratedじゃなくて良かったやつかな?
問題D – Blue and Red Balls
赤赤・・・赤赤 + 青青・・・青青 + ・・・
と赤、青の連続部分に分解します。 青の回収に i 回かかるのは、青の成分が i 個ある場合。
成分は互い違いに並ぶので、成分だけを見ると
・赤から始めて $i$ 成分ずつ
・青から始めて $i$ 成分ずつ
・赤から始めて 青が $i$ 成分、赤が $i+1$ 成分
・青から初めて 青が $i$ 成分、赤が $i-1$ 成分
の $4$ 通り。場合分けを固定すると、色の振り分け方の計算は、赤青それぞれで次の問題と同値です:
整数 $a$, $b$ が与えられる。 \[ x_1+x_2 + \cdots + x_b = a\] となる自然数 $x_1,\ldots,x_b$ の組の個数を求めよ。
これは高校数学典型の数え上げで、二項係数 ${}_{a-1}\mathrm{C}_{b-1}$ が解となります。$a$ 個のものを並べて、隙間 $a-1$ 箇所のうち $b-1$ 箇所で切り離す。「自然数」を「整数」とした場合など類似の数え上げもあるので、公式を覚えるというよりは理由付けとセットで頭にいれると良いですね。あるいは競技プログラミングの舞台ですし、小さい方を全探索で計算してみて公式を調整するのでも対応できると思います。
$N = K$ などを確認して提出。
問題E – Hopscotch Addict
ある頂点に到達したときに、「けん」「けん」「ぱっ」のどの時点かという3種類の状態を区別します。「ぱっ」でゴールに到達するときの最短路です。よって、(グラフの頂点, 3種のどれか) をひとつの頂点とするグラフを作って、最短路を求めればよいです。
最初の解法 → ■
TLE になりました。いろいろと試したものの、コンテスト中には TLE が解消できず。import および 疎行列の生成までで 350ms 程度だった ので、(今回の条件下では?)scipy.sparse.dijkstra が遅いです。このような基本的な処理で、自作のループ処理の方が速いというのは不思議なのですが、何か見落としているのか…scipyが想定しているデータにいまいち合っていないのか(疎だと速いけど密だと、とか?)
ひとまず自作が遅いのでないなら問題ないし、計測等は後回し…。
一から書き直して5分ちょっとでACできたのは良かったです。過去問練習が生きた。

