| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ||||
| 結果 | AC | AC |
全体感想
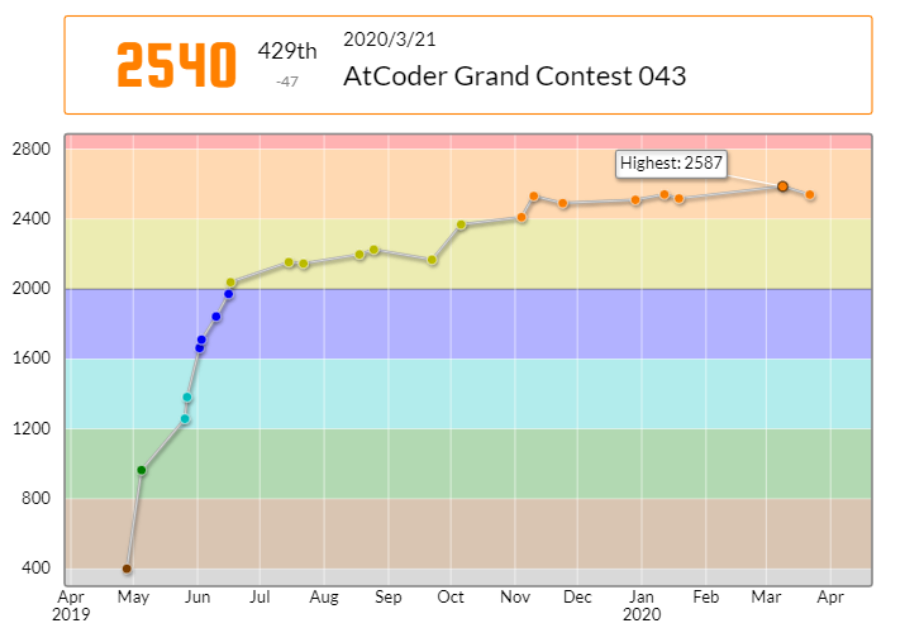
116分2完で、429位でした。
・Aを誤読して3分で提出 → WA
A+B+C の3完を上回る成績をとりたい気持ちがあったため、BCからひとつに加えて、DEのどちらかが解けるといいなという気持ちでした。一通り読んだあと、問題Bが分かりそうに思ったのと、グラフ理論に苦手意識があったため、問題BDEを中心に考えることにします。
特に、問題Eが閉曲線の連続変形という数学寄りの題材だったため、関心を持ちました。
しばらくDEを考えたあと、先に問題Bを倒します(50分)。
問題AでWAが出ていることに気づいたあと、問題Eを考えながら合間に問題Aを進め。意外と問題Aでてこずって、2完もとても遅いです。問題Eの考察もかなり初手に近いところに勘違いがあったことが判明して、色々巻き戻ってしまいました。
問題E がACできたのがコンテスト終了30分後。この問題を効率よく言語化して思考するための知識も持っていたのに、結びつけるのに長時間失敗していて、痛い敗北です。もう少しきちんと証明を考えたり、条件の判定だけなら提出で確認することもできたので、もっと落ち着いて着実に進めればよかったですね。高度数学知識が活かせる場面は競プロ初心者の私でもすこし周囲より優位がとれるところなので、こういう問題を取っていきたいんですけど、残念。
問題自体は、数学概念を良い感じの競プロ問題に落とし込んでいて、とてもきれいだと思いました。基本群がモチーフではあるのでしょうが、知識があるだけで簡単というわけでも、知識がないと無理ゲーというわけでも全然なくて、美しいバランスです。
問題B – 123 Triangle
面白い問題でした。考えたこととして、
・こういうのは、1つ1つの数の寄与に分解できるととても嬉しい
→ 隣接との大小関係によって、足し算か引き算かが分かるので難しそう
→ 偶奇くらいなら分かるかもしれない(2種の引き算の共通の性質)けど、3で割った余りだとよくわからないなあ
・実験してみる
5分くらい、いろいろ手計算しながら探ります。(しかしこの後結局、1分かからずに実験プログラムを実装したので、初めからそうしておいた方が良かったでしょうか。)
例えば「2」の個数が減少しそうかな??という気持ちになりました。しかしこれは簡単な反例があって、「020」→「22」などのように、増えてしまうこともあります。かといって、偶数の個数が減少するとも言えないです(「111→00」)。
実験プログラムを書いたあとさらに遊んでいると、やはり「2」が消えていくという観察の方向性自体は正しそうだと思いました。
今度は「答が2になるとすると…」と答から遡って考えると、一瞬で解決しました。答が2になるのは元から02のみの場合しかありません。元から02のみの場合には、全部2で割ることで、全部01の場合を解くことと同値です。(長さ 3, 長さ 4 の数列と答の一覧を作って観察しても良かったですね)。
全部の数が01のみになると、2種の引き算がどちらも足し算と見なせて、線形な操作の繰り返しなので、個々の数の寄与に分解できて、おしまいです。
ひとつずらして足し合わせる操作は、数列を多項式と見なして、$(1 + x^{-1})$ を次々とかけると思うと、二項係数が出てくる理由がより明らかかもしれません。
問題E – Topology
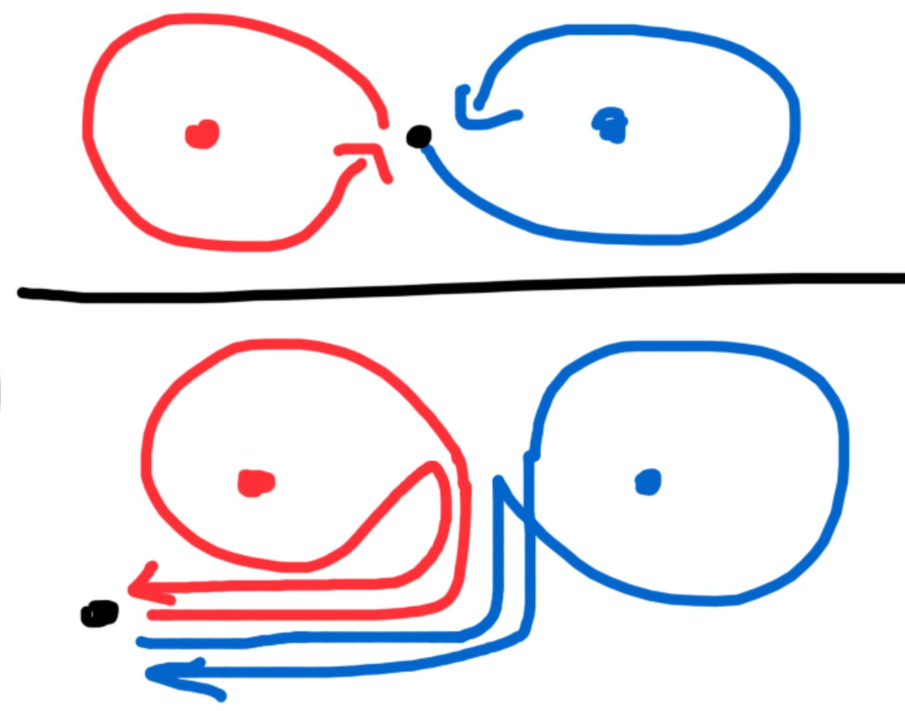
閉曲線の連続変形は、数学ではホモトピーと呼ばれます。ホモトピーでうつりあうループを同一視したときに、空間内のループを分類しようという概念が、基本群です。
$N$ 点穴の空いた平面において、どのようなループが存在するかは、完全に分類されています。
まず、適当な点をひとつ選ぶと、その点を基点(base point)とするループ全体は、ループの結合によりモノイドになります。さらにループのうちでホモトピーでうつりあうもの同士を同一視すると、ループ全体が群をなします(これを基本群という)。
平面から $N$ 点を除いた点集合(位相空間)の基本群は、各除外点のまわりを $1$ 周するループで生成される自由群であることが知られています。例えば、$2$ 点の穴をあけた場合、各除外点を $1$ 周するループを $a,b$ とすると、その基本群は「$aba^{-1}bba^{-1}b^{-1}a$」のように、$a,b,a^{-1},b^{-1}$ からなる文字列のうち、$aa^{-1}, bb^{-1}$ を含まないもの全体と同一視することができます。
考慮する穴を減らすと、この文字のうち、どれか $1$ つが単位元に置き換わります(位相空間論でいうと、空間の包含写像が誘導する基本群のあいだの準同型写像を見ています)。
例えば、除外点が 3 つあるとして、「どの 2 点を考慮してもほどけて、3 点だとほどけない」ようにするには、
$$g = a\cdot bcb^{-1}c^{-1}\cdot a^{-1}\cdot cbc^{-1}b^{-1}$$
のようにすればよいです。各点のまわりを1まわりするループを原点からとる(基点を取り換える)のも簡単で、各ループの始まりと終わりに同じ経路を加えてあげればよいです。