
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
62分6完(1ペナルティ)で88位でした。
先週から、大体わかってから詰め切るまでの手際の良さを重視して練習していますが、なかなか。Fのサイクル検出などは有名アルゴリズムだと思うのですが、考えながら初実装する形だとどうにもある程度時間がかかってしまいますね。
何はともあれ、十分時間を余して6完できたので良かったです。最近、大きな後悔を残すコンテストが多かったので。
問題B – Roller Coaster
条件を満たすものの数え上げは、
sum(condition(x) for x in iter)とbool値のsumでOKです(sumをとるときにintにキャストされる)。
地味に最近まで意識していなかった。なお、numpy なら、np.sum() よりも np.count_nonzero() の方が速いです。
問題E – Get Everything
鍵の選び方は $2^{1000}$ 通りくらいあって悲しみですが、宝箱集合は $2^{12}$ 通りくらいしかないので、この状態に対して何かを計算すると考えます。それぞれの状態から、宝箱1つ追加したときの遷移を考えると、dp更新していけます。集合を素直にset型やtuple型で持つ方法もありますが、i 番目のアイテムを持つときに $2^{i-1}$ 番目のビットを立てて整数にエンコードして扱うのが実装の簡単な方法で、特にその手法を用いる dp を競プロ方言では bit dpなどと呼ぶようです。
PyPy(231ms) : ■
Python(1485ms) :■
Python+numpy(788ms) :■
私の経験上、bit DPは np困難(numpyで簡潔に書きにくい)ことが多いです。上手く扱っている人が居たら真似をしたいなあ。
今回は、
dp[n|C] = np.minimum(dp[n|C], dp[n]+A)
と書きたい感じですが、複数箇所を並列更新するときに同一箇所を参照しているとうまく対応してくれないんですよね。

問題F – Pure
誘導部分グラフとか難しそうなことを言い出しいて、手が出ない層も多いのかなと思っていましたが、正解者数が最近の問題Fの中では最多ですか?予想よりもだいぶ正解者が多かったです。
とりあえず、手に入れたいものはサイクルであることが分かります。ただし、サイクルの関係者に制限した誘導部分グラフが条件を満たすとは限りません。[入力例3] で全ての頂点を選んだ場合がそのような例になっています。
このような場合には、頂点が全てサイクルの一部になっていることを利用すると、条件を満たしていない場合にはより小さなサイクルが見つかります。
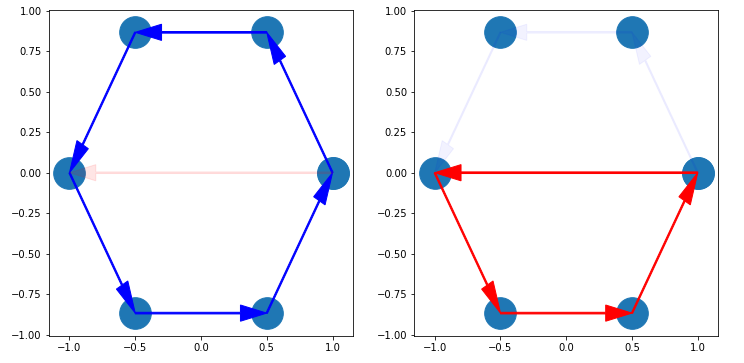
1つのサイクルから初めて、「サイクルと関係のない辺があればサイクルを小さくする」を繰り返します。「サイクルが条件を満たしていないなら必ず行ってサイクルを小さくできる」ことから、この操作をやりきった時点で所望のサイクルが手に入ります。
実装のための課題は以下の通りです。
(1) 少なくとも1つのサイクルがあるかどうかを判定する。存在する場合には具体的に見つける。
(2) サイクルに余分な辺がある限り、上述の通りサイクルを小さくする。
(2) サイクルに余分な辺がある限り、上述の通りサイクルを小さくする。
(1)は「サイクル 検出 アルゴリズム」くらいでググるといくらでも出てくる有名アルゴリズムです。私も、ちょっとどうやるのが最も一般的なのか把握していないですが、例えば
・out_deg[v] = 0 となる v は除外してよい(この v に向かう辺も合わせて消して、次数を更新)。
・頂点が1つ以上生き残って、全ての頂点のout_deg が1以上であるとする。このとき、辺に沿って移動し続けられて、行き止まりのない道 $v_1,v_2,v_3,\ldots$ が得られる。
・頂点の数が有限個のグラフであれば、$v_i = v_j$ となる $i<j$ が存在する。$v_i,v_{i+1},\ldots,v_j$ がサイクルである。
・頂点が1つ以上生き残って、全ての頂点のout_deg が1以上であるとする。このとき、辺に沿って移動し続けられて、行き止まりのない道 $v_1,v_2,v_3,\ldots$ が得られる。
・頂点の数が有限個のグラフであれば、$v_i = v_j$ となる $i<j$ が存在する。$v_i,v_{i+1},\ldots,v_j$ がサイクルである。
という要領でよいかと思います。
(2) は上で図示した通りです。辺を1つずつ見て行って、今のサイクルに絡む辺が出てきたときに、サイクルを短いものに更新します。この際、サイクルの情報として、
・頂点の集合
・各頂点の移動先
を持っておくと、1回あたりの更新を $O(1+\text{削除する頂点の個数})$ で行えます(よって全体で $O(N+M)$)。$a$ から $b$ への辺が見つかったときに、
・いま持っているサイクルにおける、$a$ から $b$ への経路上の頂点を削除
・$a$ の移動先を $b$ に設定しなおす
をやってあげればよいです。ややごちゃごちゃとした実装になってしまいましたが、バグはまりもせずAC出来てよかったです。
・各頂点の移動先
を持っておくと、1回あたりの更新を $O(1+\text{削除する頂点の個数})$ で行えます(よって全体で $O(N+M)$)。$a$ から $b$ への辺が見つかったときに、
・いま持っているサイクルにおける、$a$ から $b$ への経路上の頂点を削除
・$a$ の移動先を $b$ に設定しなおす
をやってあげればよいです。ややごちゃごちゃとした実装になってしまいましたが、バグはまりもせずAC出来てよかったです。
はじめ、1REをやらかしました。辺 (a,b) のデータを受け取るときに、
AB = [tuple(int(x) for x in line.split()) for line in readlines()]
A,B = zip(*AB)AB = [(1,2),(3,4)] という入力から、 A = (1,3), B = (2,4) と分離するような処理の簡単記法なのですが、辺データの入力が 0 件である場合にエラーを吐きます。これ、辺の個数が 0 の可能性がある問題で毎回のようにやらかしている…そろそろ要注意事項として覚えておかないと^^;

