
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | WA | AC |
全体感想
5完(3ペナルティ)で78位でした。
遅い5完ですが、Fを解いているので2桁順位。
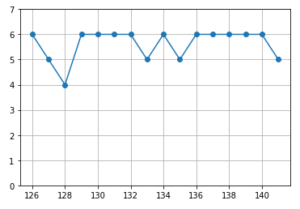
ABCコンテストの6完安定は、今の自分にとってちょうど良い目標に感じています。5連勝で途切れた、悔しい~!!
結果的には、初めての種類のバグはまりが原因だったので、コンテスト中に解消できなかったのはまぁ仕方のないところもあるか…。別実装に逃げる手もあったのですが、ratedではないのでそういう立ち回りについては後悔なし。初めての経験がひとつ増やせたので、学びのある良いコンテストだったということで。
また次戦以降、がんばるぞー(^^)
問題C – Attack Survival
1回ごとに問題文の通りにポイントを推移させようとすると、Q回にわたりN個の値の更新が必要になってTLEになります。
・1回のポイント増減 = 「全員 $-1$ したあと 1箇所 $+1$」
となります。「全員 $-1$」を $Q$ 回繰り返すことは、「全員 $-Q$」と等価なので、これをまとめてやれば計算量が $O(N+Q)$ になります。
問題D – Powerful Discount Tickets
「値段の最大のものに割引チケットを適用する」ことを $Y$ 回繰り返せばOKです。
最大値の取得するために、毎回全ての値を1回ずつ眺めると、それだけでも $O(N)$ になってしまうので、「全ての値を調べず最大値を取り出す」ためのデータ構造が必要です。リストに入れてソートすることなどが考えられますが、これだと値を書き換えるたびにソートしないといけません。
優先度つきキューを使うことで、
・値を格納しておく
・高速に最大値を取り出す($O(\log N)$ になる)
が、 実現できます。
pythonだとheapqで実装するのが普通かと思います。そのまま使うと、「最小値が高速に取り出せる」となってしまうので、$-1$ 倍して格納するなどの工夫をします。この $-1$ 倍の出し入れが混乱しやすいので、
pop = lambda: -heappop(A_minus)
push = lambda x: heappush(A_minus,-x)などを定義して実装しました。
※ ほかに、「最終的に生き残る金額最大値」を二分探索で調べるような方法もあります。チケット枚数がとても大きいときなどにも利用できて、類題がいくつかあります。
問題E – Who Says a Pun?
まず、「文字列の一致」を高速に判定したいです。
これには例えば Rolling Hash という方法があります。これは例えば「確率 $1 – 10^{-9}$ 以上で2つの文字列が完全一致するかを正しく判定できる」というような確率的な方法です。
適当な素数 $p$ と、適当な整数 $b$ (できれば $p$ の原始根)をとって、
・[2,3,4,2] → $2 + 3b + 4b^2 + 2b^3\pmod{p}$
といった要領で、数の並びを1つの整数(ハッシュ値)に符号化することを目指します(文字列は、文字コードをとるなどして数列に変換しておきます)。同一の数列は必ず同じ値に符号化され、異なる数列が偶然にハッシュ値を引いてしまう確率は 約 $1/p$ となります。例えば、$p = 10^9 + 7$ であれば、$10^{5}$ 回の判定を繰り返しても、$99.99\%$ くらいの確率で全ての判定を正しく行います。これで強度が足りないようであれば、複数の $p_1,p_2$ を併用するなどして、誤判定の確率を $1/p_1p_2$ 程度にすることで、$10^5$ 回程度文字列比較をしても、現実的には1度も誤判定が起こらないようにできます。
結局長さ $n$ の文字列のハッシュ値の計算に $O(n)$ かかっていてはダメですが、数列 $a_0,a_1,\ldots$ に対して、$a_ib^i$ の累積和を計算しておけば、ひとつひとつのハッシュ値を $O(1)$ で計算できます。
文字列の $[l_1,l_1+\text{len})$ の部分と $[l_2,l_2+\text{len})$ の部分の一致が判定できるようになれば、あとは条件を満たす len の最大値を二分探索します。二分探索する場合には、単調性に注意します。今回は、「$\text{len} = n+1$ で存在」$\implies$「$\text{len} = n$ で存在」はすぐ確かめられるので良いです。
「$\text{len} = n$ が実現できるか」の判定は、長さ $n$ 文字列のハッシュ値を全部計算して、同一ハッシュ値が $n$ 以上離れた位置に現れているかを確認すればよいです。
ここの処理で、ハッシュ値をソートして対応するインデックスを持ってきたのですが、stable でないソートをしてしまって失敗しました。
・WA → ■ (argsort をとるときに、同一値に対するインデックスが昇順になる保証がないため)
・RE → ■(atcoderのnumpyのバージョンが低いせいで、ソートに ‘stable’ が指定できない)
・コンテスト後AC → ■ (タプルの辞書式ソート)
stable でないソートに基づくバグはまりは、初めてやらかしました。これ、小さい場合を手元実験しまくっても見つけづらくてなかなか厄介ですね…。経験が増えました。すこし成長(^^)
問題F – Xor Sum 3
青のxorは赤のそれから復元できるので、赤だけに注目すればよいです。つまり、$A_1,\ldots,A_N$ の適当な部分集合の 和(xorに関する) としてどういうものがあるのかを考えればOKです(「空でない部分集合」が題意ですが、「空でない」は結果的には非本質的です)。
・bitwise xorは、$\mathbb{F}_2^n$ の加法。
・部分集合の 和 ということは、0倍または1倍の総和。
・したがって、部分集合の 和全体は $\mathbb{F}_2$ 上のベクトル空間。
・この基底を求めたければ、基本変形していけばよい。
・高々 $60$ 次元以下のベクトル空間なので、これで問題の大きさを格段に小さくできる。
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 23 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 36 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 66 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 65 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 23 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 36 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 66 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 66 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 36 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 23 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
「8の位」は担当者不在。「4の位」については、担当者を1つに絞ろうとすると、「32の位」や「16の位」の状況が今よりも綺麗ではなくなってしまうので、諦めます。
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 65 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 36 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 20 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
行基本変形の完成です。「もともとの4数の部分和で作れる数」が、「$65,36,20,3$ の4数の部分和で作れる数」と書き変わります。
この表示の良いところは、ある数 $x$ がこれら4数の和で書けるかどうかが簡単に分かるところです。$x$ の「64の位」を見ることで「65」を使うべきかどうかが決まり、「32の位」を見ることで「36」を使うべきかどうかが決まるという要領です($x$ の作り方は最大1通りにすぐ限定できて、それをテストすればよくなる)。また、部分和が $16$ 通りであることも同様に分かります。
入力例 1 の場合には、同様の方法をとると
| 4 | 2 | 1 | |
| 5 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
が完成形です。「部分和で作れる数」を考える際には、0しか入っていない行は捨ててもよく、
| 4 | 2 | 1 | |
| 5 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 |
こうですね。入力が $10^5$ 個あっても、「$2^{59}$ の位」から「1の位」までの60列しかない状況では、最終的には $60$ 個以下の数の問題に書き直してしまうことができます。さらに、上の方の桁の担当者を順に見ていくことで、問題の状況に応じた理想的な部分和を実現することができます(「理想的な部分和」が何なのか→「赤と青の和が大きいのはいつか」が少しややこしい($\mathbb{F}_2^n$ の和と $\mathbb{Z}$ の和が混ざるので)ですが、あとはそこを乗り越えればOK)。
バージョン違いに依存するWA・REは、手元環境だけだと発見しにくいですが、今回は早期に決定できました。コードが短かったですし。コードの前半部分だけ投げてREが出るかなど提出を利用したデバッグも、バグ箇所の特定に有力ですね。

