| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
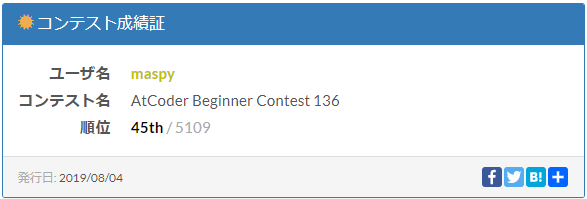
86分6完(3ペナルティ)で45位でした。
いつもと別PCでやったら、イージーミスをちょいちょいしました。
Fのコード書き終わってから提出までに5分くらいかかったり、その過程でうっかり問題AにFのコードを投げてWAを食らったり(笑)
Eはいつもよりも難しめと感じました。
問題B – Uneven Numbers
上手に数式を作ることもできますが、全探索によるナイーブ解法でもOKです。自然数 $n$ の桁数は、例えばlen(str(x)) として表せます。
問題C – Build Stairs
広義単調増加数列のことを、「単調非減少」という流儀は初めて目にしました。ググったけど、確かに世の中に存在する流儀っぽい?
基本的に、低くできるなら都度低くしておいた方が有利な貪欲戦略です。
問題D – Gathering Children
それぞれの人の最終状態を考えます。最終的に、どこかの「RL」にはさまれて、無限に右往左往することが分かります。
初期位置が L ならば、左に進んで「RL」が見つかったところでつかまります。
初期位置が R ならば、右に進んで「RL」が見つかったところでつかまります。
ある場所より左・右にあるR、Lの位置を全マスに対して事前計算しておけばOKです。
問題E – Max GCD
任意に大きくできない理由とかを考えているうちに、数列全体の総和が不変量だと気づきます。したがって、総和の約数 $d$ に対して、すべてを $d$ の倍数にできるかをテストすればよいです。
このためには、「全部を $d$ の倍数にするための操作の最小回数」が求められればよいです。例えば入力例 4 の数列を全て 5 の倍数にするには、次のようにすればよいです:
最初の数列:[1 7 5 6 8 2 6 5]
5で割った余り:[1 2 0 1 3 2 1 0]
ソート:[0 0 1 1 1 2 2 3]
0除外:[1 1 1 2 2 3]
ここから操作を開始します。それぞれ $d$ の倍数にするために、引き算か足し算で近づけることになります。引き算で使うもの、足し算で使うものどちらも1つ以上存在します。$a < b$ で、$a$ を足し算、$b$ を引き算で調整するのは得になることはありません。よって、最大値は足し算、最小値には引き算をしていきます。
合計0回の操作:[1 1 1 2 2 3]
合計1回の操作:[0 1 1 2 2 4] → [1 1 2 2 4]
合計2回の操作:[0 1 2 2 5] → [1 2 2]
合計3回の操作:[0 2 3] → [2 3]
合計5回の操作:[0 5] → []
ここから操作を開始します。それぞれ $d$ の倍数にするために、引き算か足し算で近づけることになります。引き算で使うもの、足し算で使うものどちらも1つ以上存在します。$a < b$ で、$a$ を足し算、$b$ を引き算で調整するのは得になることはありません。よって、最大値は足し算、最小値には引き算をしていきます。
合計0回の操作:[1 1 1 2 2 3]
合計1回の操作:[0 1 1 2 2 4] → [1 1 2 2 4]
合計2回の操作:[0 1 2 2 5] → [1 2 2]
合計3回の操作:[0 2 3] → [2 3]
合計5回の操作:[0 5] → []
このように、先頭と末端だけいじって、$d$ の倍数になったものを除外していきます。$2$ 元以上あれば $1$ つ減らせて、$1$ 元以下になった場合はすべて $d$ の倍数です(これは $d$ を総和の約数でとった場合)。ひとつの $d$ に対して、$O(N)$ で最小回数を計算できます。
結局のところ、前半どこかまでが引き算側、後半どこかまでが足し算側です。したがって、逐次的な操作をしなくても、この境界を調べるだけでもよい問題のようです。
[0 0 1 1 1 2 2 3]
問題F – Enclosed Points
$f(T)$ は、適当な条件を満たす点 $P$ の個数。
したがって、$\sum_{T} f(T)$ は、適切な条件を満たす組 $(T,P)$ の個数です。
したがって、$\sum_{T} f(T)$ は、適切な条件を満たす組 $(T,P)$ の個数です。
これを、$P$ 側から数えてあげる。同じものを別の見方で数えるというのはよくあるテクニックでしょうか。各 $P$ に対して、
「$S$ の 部分集合 $T$ の bounding box が $P$ を含むような $T$ の個数」
を数えて足します。
「$S$ の 部分集合 $T$ の bounding box が $P$ を含むような $T$ の個数」
を数えて足します。
部分集合 $T$ の bounding box が $P$ を含むかどうかは、$P$ の左上・左下・右上・右下 の 4 領域の点をそれぞれ使っているかどうかだけで判定できます。左上の点を1つ使っていようが、2つ使っていようが判定には影響しません。したがって、次の課題があります。
(1) 各点 $P$ に対して、左上・左下・右上・右下の点の個数を求める。
(2) それをもとに、条件を満たす部分集合 $T$ の個数を求める。
(1) について。「左上 + 左下」「左下 + 右下」など、つまり左側・下側の点の個数は、$x$ 座標、$y$ 座標でソートしたときの順位なので簡単です。あとは4領域のうちどこかが 1 領域が必要です。左下を数えることにします。これは転倒数ライクな値です。この計算は BIT で行えます。x座標が小さい方から順に見て行くとき、各時点で、ある区間に存在する元の個数を取り出せます。
BITは、ARCのC難易度の問題などでさんざん登場します。ただ、ABCコンテストで使用したのは、過去問を含めても初めてです。
(2) について。4 領域に存在するかどうかの内訳ごとに、$T$ が条件を満たすのかどうかを判定すると、結局「$T$ が $P$ の左側・上側・右側・下側 に完全に収まっている」ときが反例になると分かります。したがって、(2) は包除の原理により計算できます。

