
| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ||
| 結果 | AC | AC | AC | TLE |
全体感想
101分3完で80位でした。
1ヶ月ぶりに、レート2000以上も対象となるコンテストだったので、気合十分でした。
ここ数週間、過去問をかなりがっつり取り組んでいたこともあり、実力アップにも期待していましたが、うーん、どうだったのだろう。普段のABCコンテストと似た順位でしたが、パフォーマンス値はそれよりも高めに出ました。3問で満足するのは目標意識が低い気もするけれど、あと1問安定して解ける実力には遠く及ばない気がする。
結構、実例構成を頑張って考えるゲーに寄っていた変わったセットという印象でした。ただ、AGCはほとんど参加も過去問も経験がないので、いつもと比べてどうとかはよく分かりません。
問題A – XOR Circle
xor による和 ($\oplus$と書くことにする)は、
\[ a\oplus c = b \iff a \oplus b\oplus c = 0 \iff c = a\oplus b\] を満たすので、「両端から真ん中を決める」は無視して、「$a$, $b$ の次に$a\oplus b$ を書く」と思って考えました。結局は円状ではなく区間であれば、
\[ x, y, z, x, y, z, \ldots \] と周期3で回ることが分かります。
最終的には、次の3タイプに分けて実装しました。
・全て 0 :$0, 0, 0, 0, \ldots$ と並ぶ。
・$0$ がある:$0, x, x, 0, x, x, 0, x, x, \ldots$ と並ぶ。
・$0$ がない:3つの異なる数 $x, y, z$ が $x,y,z,x,y,z,x,y,z,\ldots$ と並ぶ。
易しい問題ではありますが、議論の漏れがないようにしっかりと場合分けをして処理しなければならず、ミスの起こりやすい問題だと思います。例えば、うっかり「$N$ が $3$ の倍数であることが必要」とかやるともうダメですし。
私も $x\oplus y\oplus z = 0$ の判定を書き忘れて1度 WA を食らいました。
問題B – Even Degrees
偶数個ずつだし一筆書きっぽい、とか、辺を加えて一筆書き、とか考えるも、全然役立ちませんでした。そもそも通常は、一筆書き可能性を次数に帰着させると嬉しい!っていう方向なので、逆の言い換えは望みが少なかったかもしれない。
手頃なグラフで実例を作ろうとしてみると、局所的には成り立つようにしていけるという当たり前の気づきを得る。最後の方で確率1/2で貼り合わない、みたいなやつ?
逆再生して、空グラフに2本セットで辺を追加していくことを考えて、不変量を探そうとする。次数の和が4ずつ増えることに気づく。つまり、辺の個数は偶数個でなければいけない!……いや、よく考えると当たり前だった(笑)
これが、「残り1頂点以外上手くいけば、最後も帳尻が合う」ことの根拠になることを確認。あとは、「都度、詰まないように決めていく」ところを考える。連結性を保ったまま辺を取り除いていくイメージですね。過去問を解いていた恩恵もあってか、「木グラフだと簡単」「まず全域木に帰着」というような方針が思いつきました。
最終的には、
・次数の和についての必要条件を確かめる。必要性が成り立てば構成できる。
・全域木をとる。全域木以外を適当に向き付ける。
・全域木の子から順に決めていく。根付き木のdfsは典型実装。根以外が条件を満たせば完成!
問題C – Skolem XOR Tree
・2ベキだと無理
・奇数だとできる:既に出来たものに手軽に足せる場所を探していったら、上手くはまった。
当たり前の式だが、$(2x) \oplus (2x+1) = 1$ というような式を見かけて記憶に残っていたことも役に立ったかもしれない。
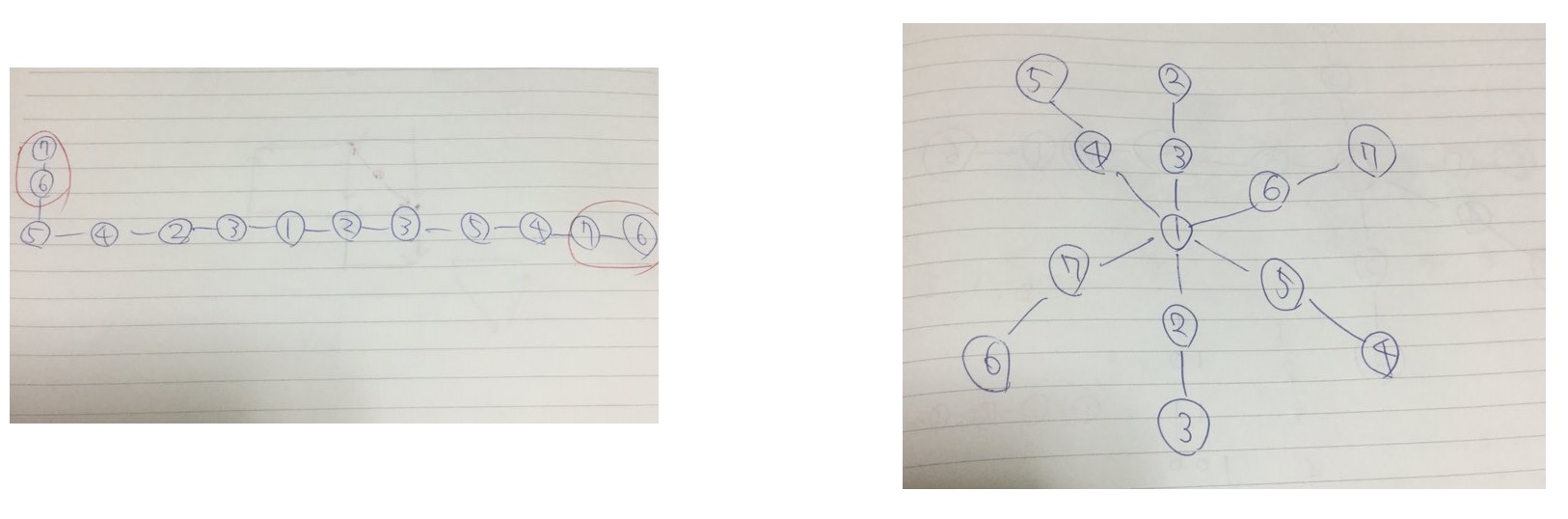 本番中のノートの画像でこんな感じ。どちらも$2x+1, 2x, 1, 2x+1, 2x$ という列を利用しています。(最後に 1 を適当なところに挿入する必要がある)
本番中のノートの画像でこんな感じ。どちらも$2x+1, 2x, 1, 2x+1, 2x$ という列を利用しています。(最後に 1 を適当なところに挿入する必要がある)$N = 6$ で詰まる。そもそも反証できるやつだったら構成を考えても空回るが、簡単な反証は思いつかないので構成できるだろうと思って粘った。
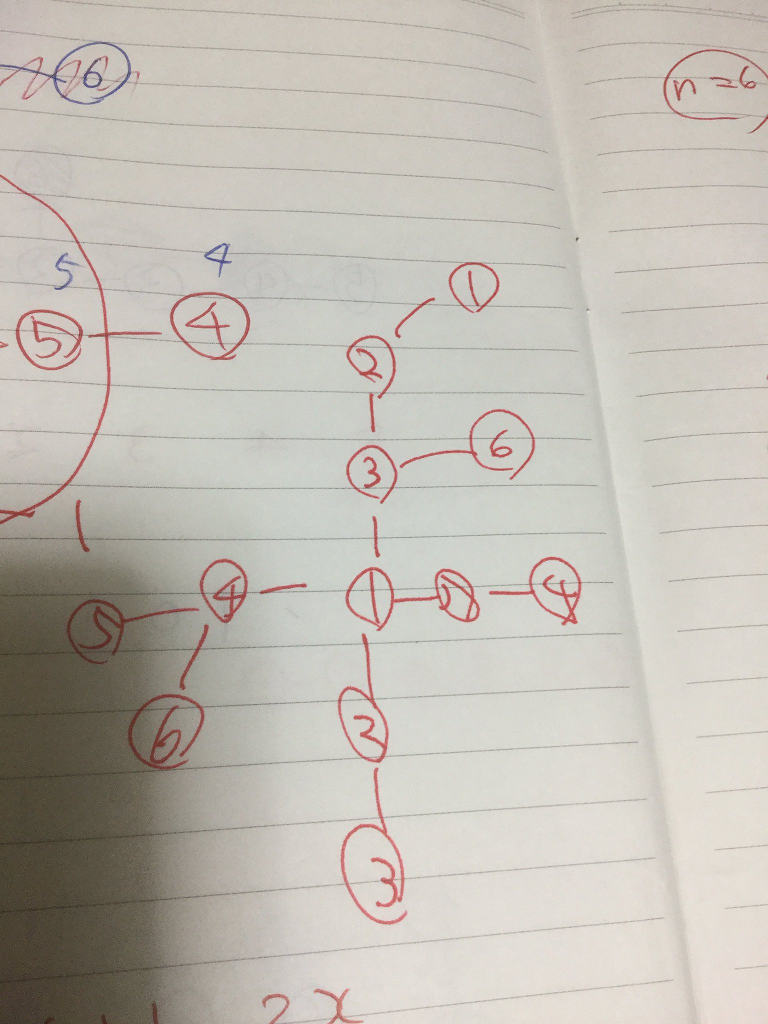
問題D – Add and Remove
残り時間も少なく、すぐには思いつかなかったので単純な再帰を書いて投下 → TLE。
a,b,c,d,… と並んでいるとき、(a,b) で使う、あるいは、a はbが更新されるまではずっと使わないフラグを立てる。ような感じで実装しました。カタラン数くらいかな?定数倍間に合わないくらいかな?と思ったけど、手元で動かした感じでは、$N = 12$ までは2秒で計算できている。
単純な再帰の実装も悩んだので、実装ミスもしているかもしれないです。

