A. Blackslex and Password
$x$ で割った余りがで添字を分類したときに，どの種類も $k$ 個以下という条件です．
ちょうど $k$ 個ずつあるときがぎりぎりで，その次が答えるものです．
B. Blackslex and Showering
すべて計算します．各要素を消したときの値は元の解からの差分更新で求まります．
C. Blackslex and Number Theory
すべてが $K$ 以上であれば，$x=a_i$ を選択することですべて $0$ にできます．
$K$ 未満の数があるとき，それは操作で変化することはありません．よって $c<K$ を固定して，$a_i\to c$ とできるかを判定できればよいです．
$a_i=c$ を除けば，$c+K\leq a_i$ が必要です．剰余で減少するときには $K$ 以上減るからです．これは十分でもあります．$x=a_i-c$ ととれるからです．
D. Blackslex and Penguin Civilization
$\mathrm{popcnt}=n,n-1,n-2,\ldots$ となる回数をそれぞれ最大化します．
$k=n,n-1,\ldots$ 順に，ある $k$ 個のビットを選び，未使用かつその $k$ ビットを含むものを昇順にすべて並べるということになります．選ぶビットも $0,1,\ldots,k-1$ の形が最適であることはすぐに分かります．
E. Blackslex and Girls
難しい．直感が働かずに，幾何をしました．
各 $i$ について使える $(a_i,b_i)$ 全体をプロットすると次のような格子点集合になります．
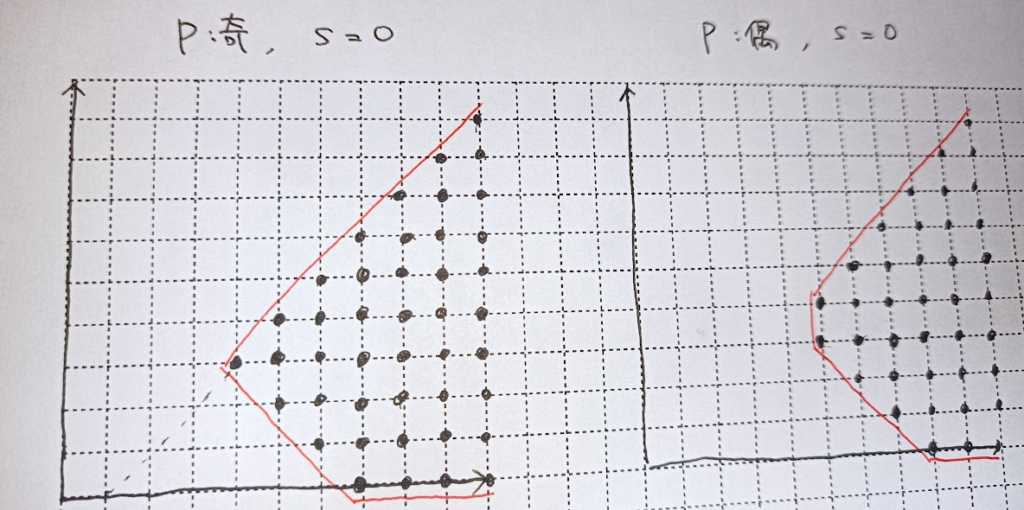
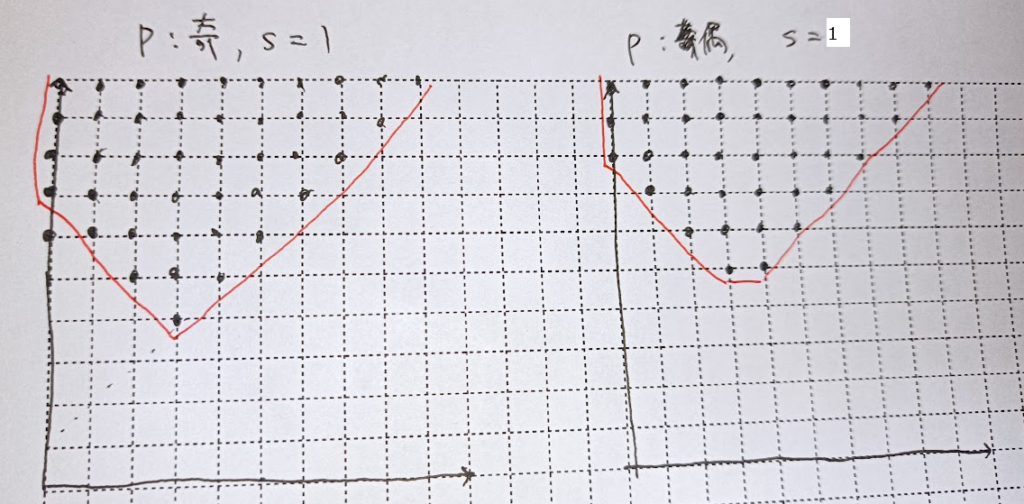
これらの格子点集合の Minkowski 和に目標の点 $(x,y)$ が入っていればよいということになります．
整数性を気にせずに凸集合の Minkowski 和をとったとき，内部の格子点はすべて作れます．一般に凸集合に対して格子点集合をとる操作と Minkowski 和をとる操作は可換ではないので微妙ですが，今回は大丈夫です．こういうのどうやって証明するのが楽なんでしょうか．定番手法は知らないです．
今回は，$S[0]=0$ としてよく，その場合 $(x,y)$ が入っていれば $(x,y+1)$ も入っています．よって各 $x$ に対して $y$ の最小値を考えて，この凸関数の min-plus convolution と思えばよいです．傾き $-1,0,1$ の境界しかないので，定義域内で $y+x,y,y-x$ の最小値が何かを計算していけばよいです．
F. Blackslex and Another RGB Walking
頂点 $1$ からの距離 $d$ にである点を $d\bmod 3$ で塗ります．
一般に頂点を距離で分類すると，距離 $d$ の頂点の近傍は $d-1,d,d+1$ の $3$ 種の距離がありえますが，本問題は二部グラフであることから，$d-1,d+1$ の $2$ 種しかありません．近傍の距離が $1$ 種ならばその方向に進めばよくて，$2$ 種あるならばどちらが $d-1$ に対応するかは決まります．
G. Blackslex and Penguin Migration
まず適当な点からの最遠点のひとつを求めます．回転対称移動を同一視すれば，これははグリッドの隅なので $(0,0)$ としてよいです．
次に $(0,0)$ からの距離をすべて求めます．$s$ から距離 $1$ の点がふたつあります．回転対称移動を同一視すれば，好きな方を $(1,0)$ としてしまってよいです．
右上隅 $(0,N-1)$ を特定します．これは $(0,0)$ からの距離が $N-1$ かつ $(1,0)$ からの距離が $N$ であるような唯一の点です．前者の必要条件で候補が $N$ 個になっているので，この部分はクエリ $N$ 回で足ります．
最後にすべての点を特定します．これは $(0,0)$ からの距離と $(0,N-1)$ からの距離から求まります．
クエリ回数は $3N^2+N$ 回になり条件を満たしています．
H. Blackslex and Plants
数列 $f$ は次のように分解できます．便宜上，$l$ をひとつずらして，$f(0)$ から足し始めるものとします．
- $0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,\ldots$
- $0,-,2,-,4,-,6,-,8,-,10,-,12,-,14,-,16,\ldots$
- $0,-,-,-,8,-,-,-,16,-,-,-,24,-,-,-,32,\ldots$
- $0,-,-,-,-,-,-,-,32,-,-,-,-,-,-,-,64,\ldots$
$k=0,1,2,\ldots$ 順に，始点から距離が $2^k$ の倍数であるところに，距離の何倍かを足すという形です．
何倍を足すかは $1,1,2,4,8,16,\ldots$ という $2$ べきからわずかに初項をいじったような倍率ですが，これは累積和が $2$ べきになるように調整したものです．
$k$ を固定して解けばよくて，「始点から距離が $2^k$ の倍数であるところに，距離を足す」ということができればよいです．足すものを $ai+b$ のようにして，$2^k$ 項ごとに見たときの区間に $a$ や $b$ を足すという処理になります．
