A. Weird Sum
色ごとに考えて,行方向と列方向について独立に考えると,$\sum_{i<j}(a_j-a_i)$ を計算するだけになります.
B. Integral Array
$y$ を固定して考えます.$x$ が good とはある列に含まれる値 $a$ に対して $\lfloor x/y\rfloor=a$ となることとします.すべての $x$ が good であればよいです.
適当な累積和テーブルを用意しておき,$a$ についてループすると,good な $x$ の個数が $O(c/y)$ 時間で求まります.$y$ についてこれをすべての $y$ について行えば $O(c\log c)$ 時間です.
C. Tyler and Strings
lcp ごとに数えます.つまり,
- $i$ 文字目より手前は完全一致している.
- $i$ 文字目は $c=s_i<t_i$ である.
- 残りは自由.
として $(i,c)$ ごとに数えることを考えます.計算量を無視すれば,適当な多項係数を足すという形で解けます.
$s_i=c$ とした場合の,多項係数における階乗逆元の積が seg[c] となるようなセグメント木を考えれば,$O(N\log N)$ 時間になります.
D. Serious Business
例えば次を順に計算すればよいです.
- ひとつの区間を使って $2$ 段目の $i$ まで進むコスト.
- ひとつ以上の区間を使って $2$ 段目の $i$ まで進むコスト.使った区間では必ず右端まで移動する.
- $2$ 段目の $i$ から,ひとつの区間を使って進み,ゴールするコスト.
$2$ 番目が易しいです.区間を使う際には $l$ でも $r$ でもソートされているような区間列を仮定してよいので,そのようにソートした上で区間内から右端に遷移させればよいです.適当なセグメント木でできます.
$3$ 番目は,$l\leq i<j\leq r$ に対して $f(i)+g(j)$ を最大化するというタイプの区間クエリができればよく,セグメント木でできます.
$1$ 番目は,$i$ を降順にループしながら,$j$ 列目で $1$ 段目から $2$ 段目に進むためのコスト cost[j] を管理することを考えます.これは常に単調減少列で,$j$ を右端とする区間があるごとに suffix に対する chmin が入る形です.これは $O(N)$ 回の区間定数加算で管理できます.
実際に最小化すべきは $cost[j]+f(j)+g(i)$ のような何かですが,これも $cost[j]+f(j)$ について同じ区間加算をしてやればよいです.
E. Air Reform
入力で与えられるグラフを $G_1$,S8 airlines のグラフを $G_2$ とします.
$G_2$ の辺重みは,$G_1$ におけるパス上の辺重みの最小値となります.答となる値もやはり,$G_2$ におけるパス上の辺重みの最小値となります.
よって,$G_2$ の最小全域木を求めることを目指せばよいです.
$G_1$ の頂点集合を小さい重みの辺から順にマージしていくときのマージ過程を考えます.重さ $w$ の辺で頂点集合 $V_1, V_2$ がマージされるとき,$V_1, V_2$ の頂点間に,$G_1$ の辺がなければ $G_2$ の $w$ の辺があります.
small to large merging で $V_2$ の点を全探索しながら,もう同じ成分となっている頂点を複数回処理しないようにしながら辺を張っていけばよいです.
F. Two Avenues
これは解説を読んで解いたのですが,なかなか読解できずに非常に苦労しました.特に $O(n+k)$ になるというあたりも理解しようとしたらとても難しかったです($\log$ をひとつ余分につけるといくらか簡単で,それでも通るようです).
DFS 木をとって,木辺と後退辺に分類します.後退辺ごとにサイクルができて,そのようなサイクルで被覆されない木辺が橋となります.
以下正のスコアを得ることを前提に場合分けして,
- 橋を $1$ つ,または橋を $2$ つとるパターン:これは簡単に計算できる.
- 後退辺を $2$ つとるパターン:これは連結集合が残るので除外.
- 後退辺を $1$ つ,木辺を $1$ つとるパターン:木辺が橋ならば最初のパターンで計算済.木辺が橋でないとして,後退辺を削除後に橋になるパターンが問題である.木辺ごとにそのような後退辺はあれば一意である.
$3$ 番目では,各木辺がいくつの後退辺に被覆されているかを数えておき,それがちょうど $1$ 個のときに何かをするというタイプの計算です.ここまでは比較的易しいです.一番難しいのは次のパターンです.
- 木辺 $2$ つを選ぶ場合.ただしどちらも元々橋ではない.$2$ つを切ることで連結成分が $2$ つに分かれるというパターン.
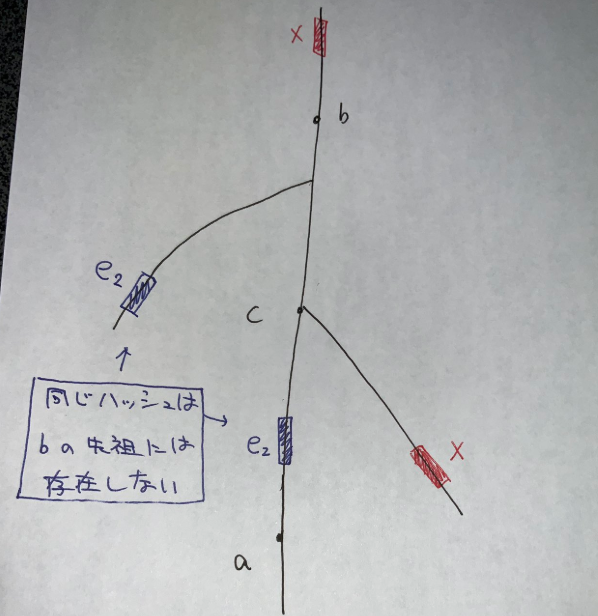
木辺を $2$ つ切ったとき,木辺だけで見ると $3$ つの連結成分になりますが,このうちどれか $2$ つが後退辺でつながっていて,全体として $2$ つの連結成分になったということです.もともと橋でなかったということは,切った辺の $1$ つをつなぎなおしても連結になることはありません.このような状況から,$2$ つの辺は次のような位置関係です.特に切る $2$ つの辺は先祖子孫の関係であることが分かります.
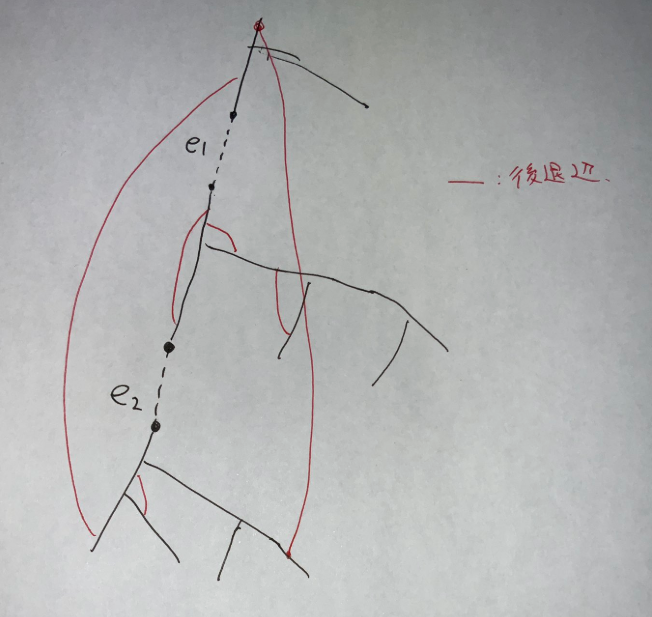
さらに,次が分かります:
- $e_1,e_2$ は橋ではなく,これらを切ると連結成分が $2$ つになるとする.このとき,$e_1,e_2$ を被覆する後退辺の集合は同一である.逆も成り立つ.
木辺だけで見たときの連結成分は上・中・下の $3$ つになりますが,上と中,あるいは中と下を結ぶ後退辺が存在しないという条件を考えるとこのようになります.
「被覆する後退辺の集合が一致」という条件がありますが,これは適当なハッシュにより扱えます.ハッシュが同一であるような辺はすべて鎖状に並び,そこから $2$ つとってスコアを最適化するという形の最適化問題になります.
大雑把な方針は次のような感じです:$score(e_1,e_2) = cnt(e_1)+2*only(e_2)-cnt(e_2)$ とする.$e_2$ を dfs で移動させながら $cnt(e_1)+2*only(e_2)$ をセグメント木で管理する($e_1$ の深さをセグメント木のインデックスとする).
$cnt(e)$ は木での最短路が辺 $e$ を通る人数.$only(e_2)$ は木での最短路が $e_2$ を通るが $e_1$ は通らないという人数.
問題点として,
- ハッシュが同じところだけを対象にセグメント木の max クエリを呼びたい(無理)
- $only(e_2)$ を $O(n+k)$ 回のセグメント木区間加算にしたい(無理)
というものがあります.どちらも工夫しないと無理です.
ハッシュは,同じハッシュの区間が交わらないという性質があります:根から $\ldots,X,\ldots,Y,\ldots,X,\ldots,Y$ のようにハッシュが並ぶことはない.
このことを使って,次のようにします.
dfs でハッシュ $X$ の辺を降りたとする.このとき,以前にも同じハッシュの辺があれば,直前のそのような辺との間の部分について,セグメント木に $-\infty$ を加算する.
$\ldots, X, \ldots, Y,\ldots, X$ となっていたとき,この $Y$ は以下の部分木の探索で絶対に登場しないからこれはやってもよいです.dfs で登るときにこれを打ち消すようにします.
このとき,セグメント木において「はじめて $X$ が現れて以降の部分」には $X$ に対応する値だけが($-\infty$ が加算されずに)有効になっています.セグメント木の求値クエリではそのような区間にクエリするようにすることで,最初の問題は解決します.
次に,$only(e_2)$ について考えます.素直にすべての辺で「$e_2$ を通るが $e_1$ を通らない人数」を管理しようとすると,更新が $O(n+k)$ 回にできません(HLD などで $O((n+k)\log n)$ 回程度にはできる).ただし,ハッシュが等しい $(e_1,e_2)$ に限定すると正しく計算されているというようにすることが目標です.
まず,人の移動は $a\to lca, b\to lca$ に分割して(人数を倍加して)しまってよいです.よって,$b$ が $a$ の祖先であるような移動 $a\to b$ だけとしてよいです.(後退辺の形ですが,最初に考えていたグラフの辺の話と混同しないように注意).
辺 $ab$ がどのような $e_1,e_2$ に寄与するかを考えます.ハッシュについて次が成り立ちます:$b$ の先祖で現れるハッシュであって,$b$ の子側にも現れるものは,鎖になる.
すると,$a\to b$ が影響するような $(e_1,e_2)$ について $e_2$ はあるパス部分にしかないことが分かります.具体的には $b$ の上下に現れるハッシュの最も深い位置での出現をとって,その $a$ との lca から $b$ までの部分です.このパスを $ac$ とします.
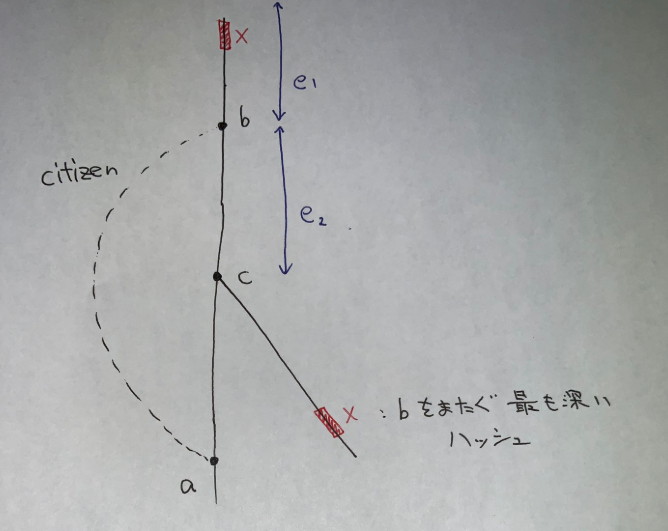
$b$ を通るときに,$b$ までの深さの $e_1$ に $2$ を加算して,$c$ の部分木に行くときに同じような $e_1$ に $-2$ を加算するようにすると,目標を達成できます.このようにすると,辺 $ab$ 上にない $e_2$ でも $only(e_2)$ の加算を行っている,あるいは辺 $ab$ 上の $e_2$ でも $only(e_2)$ の加算を行っていないような $e_1$ が出てきてしまう可能性はあるのですが,そのような辺は $b$ の部分木内でハッシュが一致して計算対象となってしまう心配はないので大丈夫です.