A. Notelock
0 に変更できてしまう場所を定義通りに数えます.
B. Make it Zigzag
prefix maximum を $c_i$ とします.
奇数番目(小さくする方)の $i$ に対して必要な操作回数を考えます.簡単のため $i-1, i+1$ 番目の項が存在するとします.
まず,すべての $i$ で生じるコストを $\max\{a_i-c_{i-1}+1,a_i-c_{i+1}+1,0\}$ とすることができます.偶数番目が $c$ になるように変換したあとで各奇数番目をデクリメントすることを考えればよいです.
個々の $i$ で見ても,最低でもコストが $\max\{a_i-c_{i-1}+1,a_i-c_{i+1}+1,0\}$ かかることを示します.$\max$ の中身それぞれについて示せばよいです.
$a_i$ に対するデクリメントを $k$ 回行ったとき,$i$ 項目は(他の操作によらず)$a_i-k$ 以上です.また $i-1, i+1$ 項目は常に $c_{i-1},c_{i+1}$ 以下です.ここから証明できます.
C2. No Cost Too Great (Hard Version)
$b$ が昇順になるようにソートします.
まず $b[0]+b[1]$ というコストで目標達成可能です.$a[0], a[1]$ を偶数にすることを考えればよいです.
以下,これより安い方法だけを考えればよいです.よって次の $3$ 種で十分です.
- コスト $0$ で目的達成している.
- コスト $b[0]$ を何回か払う.
- 唯一の $i$ に対してコスト $b[i]$ をちょうど $1$ 回払う.
それぞれ,$a[i]$ や $a[i]+1$ を素因数分解してそれらが持つ素因数を求めることでできます.
マルチテストケースなので,テストケースごとの計算量に $\max a$ をつけないように注意.素数ふるいの結果は共通前計算にするなどして対応できます.
D. Catshock
ゴールを根とする根付き木を考えて,消せる葉を消して木を小さくしていくという雰囲気で解けます.
cat が居る頂点を消さないようにするには,cat の depth の parity を管理して,消したい葉と同じ parity に居るときは操作 1 でスキップするようにします.
深さの降順に処理すれば,葉ごとの操作回数を $2$ 回を基準として「スキップ」が発生する回数だけ操作が増えます.これは,深さが切り替わるタイミングにしか生じないため,全体で $3n$ 回でおさまります.
E. No Mind To Think
ソートしておき,適当にタイブレイクして議論します(よって中央値を表す項は常に一意に確定するとします).
$x=2t+1$ とします.一度以上中央値として選ばれる値のうち最大のものを $v=a[i]$ とします.すると,$a[i]$ より大きな値のうち $t$ 個以上が,$v$ に変化します.$a[i]$ 未満の値のうち $tk$ 個以下が $v$ にできます.ここから,$x=2t+1$ と $v=a[i]$ を両方決めたときの最適解の様子が決まります.
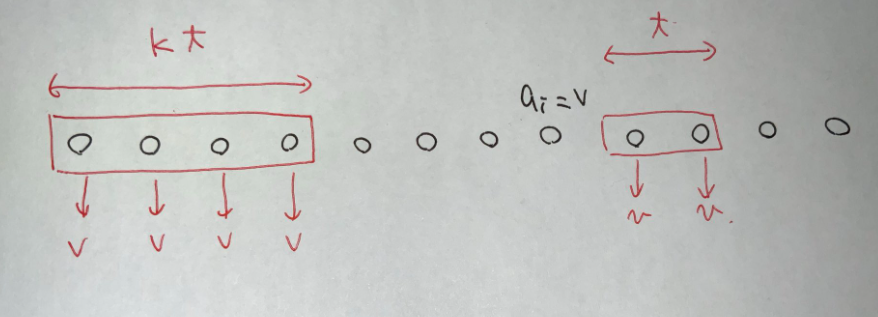
$(i, t)$ について全探索では計算量がまだダメなので,何とかします.
$i$ を固定して $t$ を最適化することを考えると,これは $t$ の上限ぎりぎりを除き,$t$ に関する上凸関数となることが分かります.
$t$ を増やしていくと,右側は減少幅が大きくなっていく(傾きが減っていく),左側は増加幅が減っていく(傾きが減っていく)からです.
よって三分探索などの凸最適化を行えばよいです.
F2. Bombing (Hard Version)
列の数え上げの問題ですが,少し変更した次の問題を解きます:列およびその塗分けの組であって適切なものを数えよ.
条件を満たす列について,たいていの場合はその塗分けは一意なので,最後に $(1,2,\ldots,N)$ に対する調整をすればよいです.
また,私は $p$ の左右に $0, n+1$ を補うことで,次のようにしました.
- $p_0=0$ は色 $1$ であり,$p_{n+1}=n+1$ は色 $2$ である.
後述の解法でも少し両端の処理分けが減るかなと思います.
$[0,x-1]$ が色 $1$ かつ $[x,n+1]$ が色 $2$ であるような唯一の $x$ を考えて,その場合の答を $F(x)$ とします.$ANS = \sum F(x)$ なので,各 $x$ に対して $F(x)$ が求まればよいです.
$p_i\neq -1$ となる $i$ を $i_0,i_1,\ldots,i_k$ として,$F(x) = \prod_j F_j(x)$ のように表します.$F_j(x)$ は,$[0,i_j]$ 部分が適切に定められている前提で,$[i_j,i_{j+1}]$ 部分を適切に定める方法の数え上げです.
$x$ を決めると,$i_j$ 番目の色が確定します.これが色 $1$ ならばそこまでの色 $1$ の個数が分かり,色 $2$ ならばそこまでの色 $2$ の個数が分かります.添字を見れば合計個数が分かるので,色 $1,2$ 両方の個数が分かります.よって,$x$ を固定すると $F_j(x)$ は適当な二項係数としてかけます.
これを高速化する(F2 のため)には,$L=i_j$, $R=i_{j+1}$ として $F_j$ が $O(R-L)$ 個の定数区間として書けることを確認すればよいです.$x$ が $p_{i_j}, p_{i_{j+1}}$ の間のときに二項係数の式が $x$ 依存になるのですが,そのうち $0$ でない値が出てくるものは $R-L$ 個以下であることが式を書けばすぐに確認できます.これらを個別更新,その他の区間を双対セグメント木などで区間更新すればよいです.
$O(N)$ 時間で解けるはずですが,$O(N\log N)$ 時間でも十分でした.

