A. Mix Mex Max
まずこのような 3 つ組が何者かを考えます.
$\mathrm{mex}=m$ が $1$ 以上になるとき,最小値は $0$ です(mex が $0$ ではないので).よって条件から最大値は $m$ です.これは $\mathrm{mex}=m$ に矛盾します.
結局 $\mathrm{mex}=0$ しかありえず,$3$ つ組は $[x,x,x]$ かつ $x\geq 1$ というものしかありません.列全体は $0$ でない値の定数列にすることになります.
B. Hamiiid, Haaamid… Hamid?
おおよそ次の $2$ 通りを考えます.
- 人の左隣に壁が作られる.脱出者は初手でどちらかの方向を選び,最寄りの壁に進み,そのあとは $1$ 歩ずつ進む.
- 人の右隣に壁が作られる.脱出者は初手でどちらかの方向を選び,最寄りの壁に進み,そのあとは $1$ 歩ずつ進む.
このときのコストは,人のインデックスおよび左右の最寄りの壁の位置から計算されます.その最大値が実際に壁作成者が達成可能になります.
C. Trip Shopping
まず $k\geq 2$ のとき,Alice は $2$ 回目以降の操作は $1$ 回目と同じ場所を連打するとしてよくて,$k=1$ に帰着できます.
Bob は選ばれた 2 箇所について,大きいもの $2$ 個をプラス,小さいもの $2$ 個をマイナスとして使うことになります.
適当にタイブレイクしておきます.Alice は次を最適化します.
- $t$ を適当にとり,$t$ 以下のものを色 $0$,$t$ より大きいものを色 $1$ とする.
- $2$ つのインデックスを選ぶ,ただし色 $0, 1$ が合計で $2$ 個ずつあるようにする.
- このときに Bob が増やせる値を最小化せよ.
$t$ をインクリメントして要素の色を変えながら,色 $1$ が $0, 1, 2$ 個あるようなインデックスに対する何かの値の最小値を管理することで解くことができます.
よく考えると色 $1$ が $1$ 個ある場所については損失 $0$ なので,もう少し簡単にできたかな.
D. Root was Built by Love, Broken by Destiny
木でない場合は不可能です.木だとします.
木 DP をします.次数 $2$ 以上の頂点を根にとると少し簡潔になると思います.
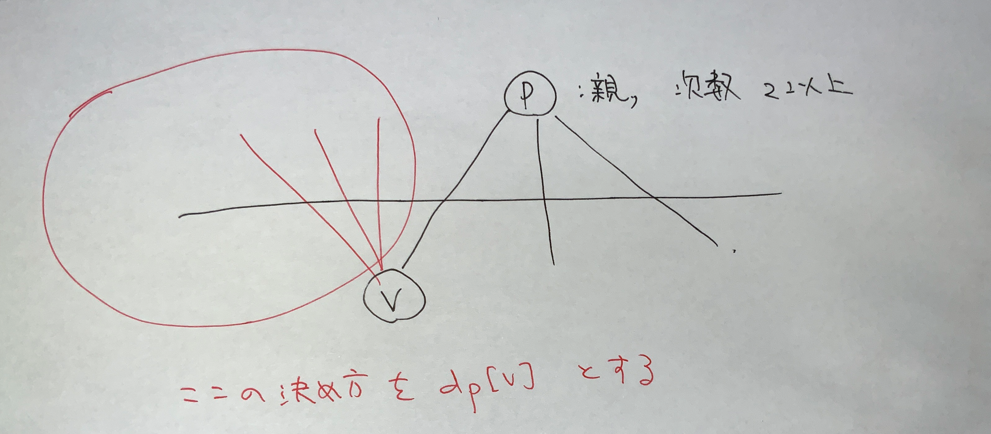
$\dp[v]$ を上のように定義します.あとは,次数 $2$ 以上の子は左端に置くしかないことに注意して計算します.
E. Ancient Tree
葉から bottom up に決めていきます.
$v$ の色を決めるとき,subtree に存在する色と同色にしておけば,その親以降で損をすることがないというのがポイントです.
よって,subtree 内ですでに色を決めているとき
- $2$ 方向にある色が複数あるなら,その点でコストが発生することは諦める.subtree 内に存在する色で塗る.
- $2$ 方向にある色がちょうどひとつあるなら,それと同じ色で塗る.コストは発生しない.
- $2$ 方向にある色が存在しないなら,subtree にある適当な色で塗る.コストは発生しない.
という要領です.
subtree にも $v$ 自身にも色がないときにどうするのかという問題がありますが,これはあとで適当な先祖のところでの都合に合わせて適当な単色で塗るようにすればよいです.これらを熱烈実装します.
subtree に配置された色集合を返り値としてマージテクを利用した木dpで実装しました.
F. Hamed and AghaBalaSar
苦戦.
とりあえず最大値 $c$ とその個数 $n$ を決めてみます.$\binom{N-1}{n-1}$ 通りの $c$ の配置がありえます.
- 「$c$ の直前が $c$ ではない」という事象が発生している場所の個数の期待値.
- そのような場所について,その $c$ までで発生するコストの期待値.
- $c$ 以外の場所を $c-1$ 以下で埋める方法の数え上げ.
の積として求めたいものがかけます.
最初の値は,$n(N-n)/(N-1)$ です.右端に置く $c$ も含めて,$(N-n)/(N-1)$ ずつです.
$2$ 番目の値は,そのブロックの先頭に置かれることになる値の期待値が $(M-nc)/(N-n)$ であることから決まります.最後の値は,$[x^{M-nc}](1+x+\cdots+x^{c-1})^{N-n}$ です.
もろもろやった結果,私の帰着先は以下のような問題でした:
$$\sum_n [x^{M-nc}]\binom{N-1}{n-1}\cdot n\cdot (1+x+\cdots+x^{c-1})^{N-n}$$
これを $\sum_n [x^{M}](x^c)^n\times \cdots$ のようにして,二項定理などで変形すると,
$$\sum_n [x^{M-c}](1+\cdots+x^c)^{N-1} + (N-1)[x^{M-2c}](1+\cdots+x^c)^{N-2}$$
のようになりました.結局 $[x^{m}](1+\cdots+x^c)^{n}$ のような計算に帰着され,これは $(1-x^{c+1})/(1-x)$ と見て分子を二項定理で展開することで $O(m/c)$ 時間で計算できます.
全体の計算量は $\sum_c \lfloor M/c\rfloor$ で $O(M\log M)$ 時間となります.
G2. Inter Active (Hard Version)
G1
$k$ 番目を無視しないとすると,$Q$, $\mathrm{rev}(Q)$ に対するクエリの和が $N$ になるということを利用します.$k$ 番目を無視したことによってこの和が $N$ からずれて,ここから何らかの情報を取り出すという戦略です.
$k=N/4$ 程度にとって,$k$ 番目に $v$ を置き,
- query1:$A, v, B, C$ の結合($|A|=|C|=k-1$)
- query2:$\mathrm{rev}(C), v, \mathrm{rev}(B), \mathrm{rev}(A)$ の結合
とします.これらの和を求めると,$B\to v$ 辺が存在するかが分かります.よって二分探索すれば,$v$ に入る辺を決定できます.
$v$ ごとに $O(\log N)$ 回で全体のクエリ回数は $O(N\log N)$ 回です.
これで G1 は AC になりました.手元で試すと $10.6N$ から $11.0N$ 回程度となっており,G2 まであと少しです.
G2
G1 から小手先の効率化を考えてもなかなかうまくいきません.これは途中で気づいたことですが,$\log(100!)/\log 2$ が $525$ 程度であることから,「$2$ クエリあたり $1$ bit の情報量(ひとつの bool を得る)」という考え方だけでは絶対に解けないということになっています.
次に考えたことは,$1000$ 回の質問時点で $85$ 項程度は確定できるので,残りの項は適当な Heuristic によりこれまでの質問と矛盾しない解を無理やり見つけるという方法です.これはすべてのクエリの返り値を利用できるので情報量は足りているだろうと考えていました.しかし実はこれも失敗です.グラフが $50$ 組のマッチングからなるとします.長さ $2$ のサイクルについてはどちらかを $k$ 番目に置くことがない限り,その連結成分はクエリ結果に常に $1$ の寄与をするため,そのようなサイクルが複数残ってしまったときに区別の方法がありません.ランダムケースは上手くいくのでなかなか気づきませんでした.
というわけで,$2$ 回より少ない回数で $1$ bit の情報を得るという感じの方法を考えます.
$P[a]=b$ となる $a,b$ が分かっているとします.第 $k$ 項に $b$ を置くことにします.
- $a, X, Y$ と並べたあと $k$ 項目に $b$ を挿入したもの
- $X, a, Y$ と並べたあと $k$ 項目に $b$ を挿入したもの
のクエリ結果を比べます.$a\to b$ 辺の寄与を除いてからこの $2$ 通りを比較します.これらではおおよそ $X\to a$ 辺と $a\to X$ 辺の個数が違いとして現れるのですが,$a\to b$ 辺があると分かっている状況では単に $X\to a$ 辺の個数が得られるということになります.
これで二分探索可能になっています.これは一見するとやはり「$2$ クエリで $1$ bit」という情報量を得ているだけですが,片側のクエリが二分探索中で常に一定にできるため最初の定数回を除き $1$ クエリあたり $1$ bit の情報を得ることができます.
G1 での解法でひとつの辺を見つけたあと,この方法でパスを延長していってサイクルを確定させるという手順をとることで,連結成分のうちひとつ以外の点ではこちらのアルゴリズムを適用できます.
私の提出では,ジャッジ内のテストケースに対してクエリ回数 $814$ 回以下を達成しているようです.
H. 23 Rises Again
怪しい Heuristic 的解法です.
まず $M\leq 79$ であることが分かります.
- 全域木をとる.
- ここからひとつ辺を足すごとに,「頂点とサイクルの組」が $3$ 個以上ずつ増えていく。
- 「頂点とサイクルの組」は $150$ 以下なので,全域木に足せる辺は $50$ 個以下.
合計 $2M$ 個の辺を考えて,独立集合問題にします.
- 同じ辺の向きだけ逆のものは同時に選べない
- どの頂点でも入次数は $1$ 以下
- どの頂点でも出次数は $1$ 以下
これで $2M$ 頂点の最大独立集合問題が解ければよいということになります.
最大独立集合は $100$ 頂点前後くらいならまあまあ解けるだろうという感覚のもと,最大独立集合 solver を持ってくると AC になりました(実は $79$ 頂点というつもりで投げたのですが $158$ 頂点の勘違い…実際のテストケースはすべて $M\leq 50$ っぽい?).計算量保証のできていない解法ですが,落とすのは難しいだろうなあ….
その他,「辺をランダムに並べて貪欲に使っていく」「辺を使うかどうかを rollback dfs で探索」などさまざまな解法が通っているようです.
まとも解法情報(Nachiaさん):https://x.com/NachiaVivias/status/1953528760621498649

