概要
問題文 → ■
公式解説 → なさそう?
自分の提出 → ■ (950768 点)
Heuristic contest タイプの問題で、厳密解が得られなくともそこそこ良い解を出力することが要求されています。
本番時間内の順位表基準で、トップスコア以上になりました。本番後の提出を合わせても、2021 年 4 月現在で、ぎりぎり 1 位スコアみたいです。
解法
置き方の全列挙
「積の和」なので、大きな積でがっつり稼ぐのが基本っぽいです。したがって、全配置のうち積が最大となるものから置いていく貪欲法を考えました。
「全配置」って全列挙できるのかな?ということで、[polyomino] でググって調べたところ、大きさ $8$ のミノは、回転や対称を同一視しない場合で $2725$ 通りあることが分かります。全計算して、ソースコード埋め込みなどもできそうです。
実際には、かなり雑に生成しても $100$ ミリ秒かからず生成できました。同じミノに対する表現が一意になるように、$x$, $y$ 座標の $\min$ が $0$ になるように生成していきます。いろんなマスの $4$ 方向隣接を追加していくだけです。
def gen_polyomino(n):
if n == 1:
yield ((0, 0), )
return
se = set(gen_polyomino(n - 1))
dxdy = ((1, 0), (0, 1), (-1, 0), (0, -1))
for P in se:
me = set(P)
for x, y in P:
for dx, dy in dxdy:
to = (x + dx, y + dy)
if to in me:
continue
Q = P + (to, )
min_x = min(x for x, y in Q)
min_y = min(y for x, y in Q)
Q = ((x - min_x, y - min_y) for x, y in Q)
Q = tuple(sorted(Q))
yield Q効率はともかくとして、今回の目的ならこの程度の実装で大丈夫でした。
貪欲法
mino が $2725$ 種あり、置き方の起点が $2500$ 通りあるので、雑に見れば大体 $2700\cdot 2500$ で $7\cdot 10^6$ 通り程度の置き方がありそうです。このうち、壁を突き破るものや、「$0$」を含むものを除きます。手元のランダムケースでは、置き方は $2.8\cdot 10^6$ 通り程度でした。$0$ を含まない確率が $0.9^8 = 0.43$ 程度と見積もってもそのくらいですね。
このくらいでしたら、全部ソートすることが可能です。全置き方を、置けた場合に得られるスコアでソートします。ソートしたら、その順にしたがって貪欲に置いていきます。

これで、94.3 万点(順位表 7 位相当)が得られました。
ランダム要素の追加
貪欲法では、積の大きなパターンから順に試していくことになります。ところで、「積」としてありうる値はかなり限られています。

「一桁の整数 $8$ 個の積」としては、$2026$ 通りの値しかありません。一方、上述の貪欲法では、$3\cdot 10^6$ 通りのパターンのソート順を利用しています。したがってこのソートには引き分けの値がかなりたくさん存在して、同じ貪欲アルゴリズムでも容易に乱数要素を含めることができます。
積の値が一定の部分をシャッフルしながら、貪欲法を完全にやりなおして、当たり待ちをします。

これで、950768 点を出すことができました。
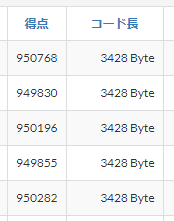
同一コード 5 回の提出で、このくらいばらけました。たくさん提出することでスコアが上がる余地がありますね。
ところで
[入力例 1] に対するスコアは、採点スコアの 2 割くらいしか出ていないんですよね。何でだろうと思って確かめてみると、[入力例 1] は生成方法が採点用データと異なるようです。
2, 3, 4 がたくさん生成されていて、8, 9 はかなり少ない盤面となっているようですね。ちゃんと生成器をダウンロードするか、自分でランダム生成するかをしないと、施策の改善が評価できなくていまいち。
その他反省。
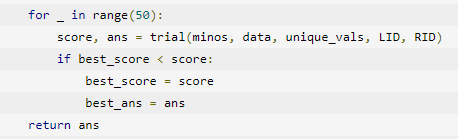
試行回数を増やしても、スコアが改善しないやつに気づかず頭が悪い。return best_ans に修正しましょう。

