ニワンゴくんとゲーム（第4回ドワンゴからの挑戦状本選 [D]）

概要
解法
関連

概要

問題文 → ■
公式解説 → ■
自分の提出 → ■

解法

$N$ を定数とします。次のように $\dp(x), \DP(x)$ を定義します。

$x$ から始めて $N$ を作る方法の数え上げ：$\DP(x)$
$x$ から始めて、初手が操作 $2$ または操作 $3$ である場合に $N$ を作る方法の数え上げ：$\dp(x)$

これらは、次の漸化式により大きな $x$ から順に計算できます。

$\dp(x) = \DP[2x] + \DP[2x+1]$
$\DP(x) = \DP[x+1] + \dp[x]$

特に、$\DP$ は $\dp$ の上側累積和です。例えば $N = 25$ として、次の表のようになります。

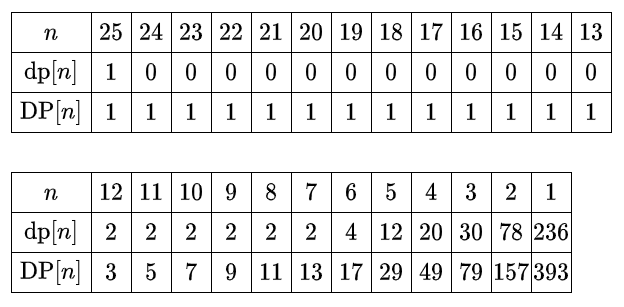
答は $\text{DP}[1]$ となります（$N = 25$ に対する答は $393$ です）。

$L_{k} = \lfloor N / 2^{k+1}\rfloor$,$R_{k} = \lfloor N / 2^k\rfloor$ とします。次が帰納的に確かめられます。

ある多項式 $f_k$ が存在して、$1\leq x < R_k – L_k$ に対して $\dp[R_k – x] = f_k(x)$
ある多項式 $F_k$ が存在して、$0\leq x < R_k – L_k$ に対して $\DP[R_k – x] = F_k(x)$

$L_{k+1} < x < R_{k}$ ならば $\dp[x] = \DP[2x] + \DP[2x+1] = F_k(R_k-2x) + F_k(R_k-2x-1)$ より $f_k$ が計算できます。$\DP[x] = \DP[R_k+1] + \dp[R_k] + \sum_{x\leq y < R_k} \dp[y] = F_{k+1}(R_{k+1}-R_k-1) + \dp[R_k] + \sum_{y=1}^{R_k-x}f_k(y)$ より $F_k$ が計算できます。

多項式 $f_k$, $F_k$ は、列 $f_k(1), \ldots, f_k(k)$ や $F_k(0), \ldots, F_k(k+1)$ を持つ形で管理します。$f_k$ の計算は $F_{k-1}$ に対するLagrange 補間、$F_k$ の計算は累積和および $F_{k-1}$ に対する Lagrange 補間から行えます。

概要

解法

関連