| A | B | C | D | E | F | |
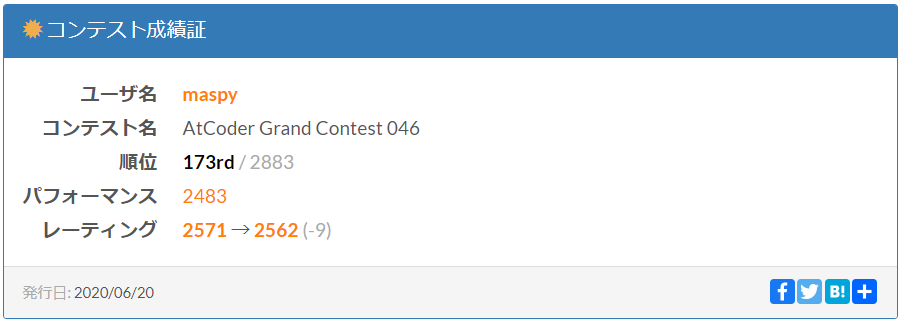
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | |||
| 結果 | AC | AC | AC |
全体感想
91分、ABC 3 完で、173位でした。
90秒 + 30 分 + 60 分。A は証明込みです、ここだけ速かった。
B, C とも結構苦戦しての AC で、そんなに簡単だとは思わなかったので、感触よりも順位がふるわずという感じです。
5連戦の収支は一応プラスですが、赤はまだまだですね。過去問に言語アプデきましたし、練習いっぱいがんばるぞ!
問題A – Takahashikun, The Strider
$r = e^{2\pi i\cdot x / 360}$ とします。移動を複素平面で考えると、$k$ 回目の移動は $r^k$ です。したがって、
$$1 + r + \cdots + r^{K-1} = 0$$
となる最小の $K$ を求めればよいです。$r\neq 1$ なので、 $r-1$ 倍することによりこれは $r^K =1$ と同値なので,$\exp(2\pi i\cdot Kx / 360) = 1$ となる最小の $K$、つまり $360\mid Kx$ となる最小の $K$ を求めればよいです。
問題B – Extension
「操作列の結果、完成図としてありうるものを数えよ」というタイプの問題です。このような問題では、複数の操作列が同じ完成図に対応しうるのが厄介です。完成図としてありうるパターンの同値な言い換えを探したり、操作に制約を加えて同じ完成図を作る方法が一意になるようにすることを目指します。
まずは、サンプル 2 から考えました。行は下方向に足すことにしました。
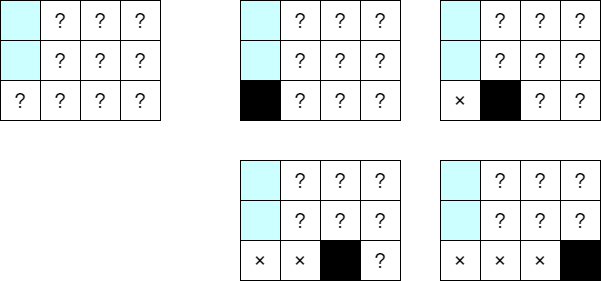
完成図で一番下の行のうち、最も左端にある ■ で場合分けです。例えば、左下隅が黒く塗られる場合、ここは初手にとるとしてよいです(そうでない操作列があったとして、初めてここを黒く塗る瞬間までの操作列を考えると、容易に初手に左下隅を塗る操作列に取り換えられる)。(ここを考察の起点としました)。
左から2番目が初出の■の場合にも、列幅を 2 に拡張した直後にここを塗るとしてよいです。
サンプル 2 の合わせ:$65 = 3^3 + 2\cdot 3^2 + 2^2\cdot 3 + 2^3$
$c,d$ を固定して、$a\times b$ の長方形を $c\times d$ に拡張するときの数え上げを、$\dp[a,b]$ として漸化式をつくります。
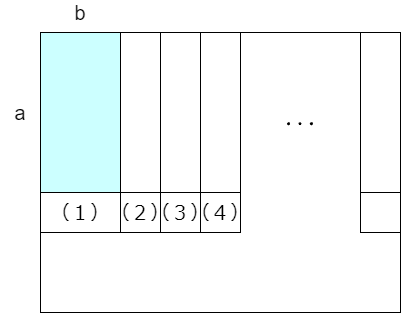
同じように次の列で初出の ■ がどこにあるかに応じて計算すると、(1), (2), … の順に式にして
$$\dp[a,b] = b\cdot \dp[a+1,b] + a\cdot \dp[a+1,b+1] + a^2\cdot \dp[a+1,b+2] + a^3\cdot \dp[a+1,b+3] + \cdots$$
という式が立ちます。これで、dp テーブルを下段から、右から埋めていく形で実装しました。$\dp[a+1, -]$ が埋まったとき、まず、(1)部分の寄与は、$\dp[a,b] \leftarrow b\dp[a+1,b]$ の形で計算できます。(2)~部分の寄与については、$\dp[a,b]$ へ足しこむ値が $\dp[a,b+1]$ へ足しこむ値の $a$ 倍に項をひとつ加えたものになっているので、大きな $b$ から順に計算することで、ひとつひとつの $\dp[a,b]$ を $O(1)$ 時間で計算できます。
問題C – Shift
条件を言い換えるところにも時間がかかったし、そのあと数え上げを考えるところにも時間がかかりました。
「抜き取って挿入することを繰り返す」系の典型的な考え方として、「挿入は最後にまとめてよい」みたいなのがあります。(https://atcoder.jp/contests/abc006/tasks/abc006_4)
$K$ 個以下の $1$ を抜き取ったあと、もとの位置よりも左に挿入するという問題になります。今回は、抜き取る数が $1$ だけに限られるというのが著しいポイントです。特に、「$0$」の位置は固定されていることが考察の起点となります。(しばらく、抜き取らなかった数とのLCSが~、みたいな考察をしてしまいましたが、下手でした。$0$ が不動…確かにそりゃそうで、すぐ気づけるべきですね。)
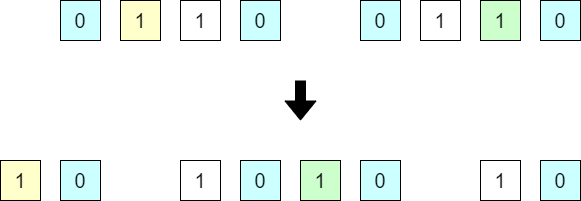
特に、各「$1$」の位置を、$0$ との関係によってとらえなおします。左に $n$ 個の $0$ があるような「$1$」の位置を $n$ と呼ぶことにすると、上の例では
・1, 1, 3, 3 → 0, 1, 2, 3
のように変換しています。
単調増加数列 $A_1, \ldots, A_n$ が与えられる。$k$ 個以下の $A_i$ を選び、$0$ ~ $A_i-1$ のどれかに変化させることができる。作れる数列を、multiset として見たものは何通りあるか
という問題に置き換わりました(かなり言い換えたので、ここで愚直実装でサンプル合わせをして検算しました)。
multiset なのが厄介なところです。問題 B のように、完成図に対して一意な操作列になるよう操作を限定することによって対応します。具体的には
・不要な変形は行わない:$a$ を $b$ に書き換え、 $b$ を $c$ に書き換える操作。
・単調性:$a>b$ として、$a$ を $c$ に、$b$ を $d$ に書き換えているならば $c\geq d$。
を課すことで、multiset を得る方法を一意に限定することができます。
たとえば サンプル 2 で考えます。[1,1,3,3] を2手まで変形する問題です。「1」の変化のさせ方によって場合分けをします。
(1)どちらの 1 もそのまま
(2)片方の 1 を 0 に書き換える
(3)両方の 1 を 0 に書き換える
(1)の場合には、[3,3] 部分は自由に変化させます。
(2)や(3)の場合は、[3,3] 部分は「1に変化させてはいけない」というルールで操作をすると見なします。
・どの数値まで操作したか
・何回の操作を行ったか
・「変化させてはいけない数」がいくつできたか
をキーとして dp を書くことができます。
操作「$a \to b$」を行うときには、$a$ だけでなく $0,1,\ldots,b-1$ も、今後変化禁止の対象となります。この部分の遷移を累積和を使ってまとめることで、$\Theta(N^3)$ 時間の解法となります。

