概要
公式解説より良い計算量になっていますね。たぶん、$3$ の指数が半分という感じ。
解法
前計算1:パスの場合
長さ $n$ のパスの場合に、次の $2$ つの値を計算しておきます。
- 端点をともに色 $0$ で塗った場合の、パス上の塗り方の数え上げ
- 片方の端点を色 $0$、もう片方の端点を色 $1$ で塗った場合の、パス上の塗り方の数え上げ
以下、$\dp_{00}[n]$, $\dp_{01}[n]$ などと呼びます。
前計算2:グラフの変形
はじめ、辺に重み $1$ をつけておきます。次の 2 つの操作を可能な限り繰り返します。
- 次数 $1$ の頂点 $v$ があれば、削除する。かわりに、最後に答に $K-1$ 倍することを覚えておく。
- 次数 $2$ の頂点 $v$ があるとき。
- 長さ $n$ の自己ループを $2$ 重カウントしているならば、終了。
- そうでないならば、その頂点に接続する $2$ つの辺を、$av$, $bv$ としたとき、頂点 $v$ を削除して新たに辺 $ab$ を張る。重みはもとの $2$ 辺の和である。頂点 $v$ は削除する。
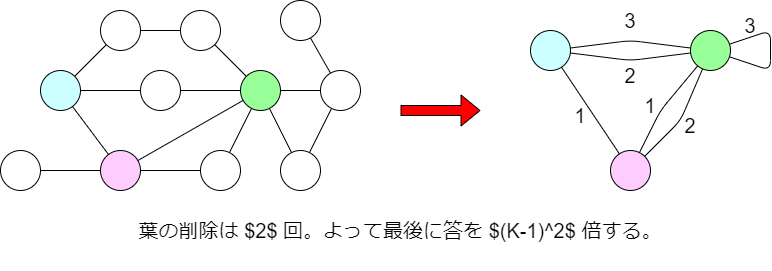
操作の過程で、連結性は維持されます。もとが木ならば終了時点で次数 $0$ の頂点がひとつ残り、もとが unicyclic ならば終了時点で $1$ 頂点と自己ループひとつが残ります。
変形後のグラフの大きさ
変形後の頂点数、辺の個数を $V, E$ としましょう。まず操作による頂点や辺の個数の変化は、頂点と辺ともに同時に $1$ 減少するパターンしかありません。よって、$E – V \leq 3$ が成り立ちます。また、操作はグラフの連結性を保ちます。よって、
- 次数 $0$ の頂点が存在する場合:連結性より頂点数はひとつ。$(V,E) = (1,0)$ である。
- そうでない場合:次数 $1, 2$ の頂点はすべて削除されているので、残った頂点の次数はすべて $3$ 以上である。$3V\leq \sum_{v}\deg(v) = 2E \leq 2V + 6$ なので、$V\leq 6$ となる。
よって、$V\leq 6$ かつ $E\leq 9$ が成り立ちます。
数え上げ
あとは簡単でしょうか。たぶん、ここは公式解説とも共通ルートです。
$V$ の塗り方を決めていきます。$|V|$ がかなり小さくなったので、ある程度まともな方法ならだいたい間に合うのではないでしょうか。$K$ が大きいので、$K^{|V|}$ 通り全探索するとかは無理ですが。
私は「すでに塗り方を決めた集合」をキーとする bit DP の形で実装しました。
$V$ の分割を全列挙するとかでも大丈夫でしょう。$V$ の点の塗り方に応じて、圧縮したパス上の塗り方($\dp_00[n]$ や $\dp_01[n]$)を掛け合わせます。
計算量
前計算は線形時間 $O(N+M)$ 時間。数え上げ パートは例えば $O(|V|3^{|V|})$ 時間で計算できます。
$|V| \leq 2(M-N)$ と評価できて、$O((N+M)(M-N)3^{2(M-N)})$ 時間で解くことができます。

