概要

えええ…正当性の保証がないことを認識した上での出題というのはどうなのと思ってしまいました。うっかり論理に穴があって出題ミス、というのならまだ分かりますが。まぁ、完璧じゃなくてもいいから気楽に出題していこうというサービスですから、仕方がないでしょうか。

なるほど。一読して、出題ミスは十分ありうるくらいの認識はしかしていなかったけれど、そもそも正当性を確かめていないもの(想定解が存在しないレベルのものも?)ある感じなのですね。
とはいえ、証明できました。
ちゃんと書き残しておいた方が良いと思うので、書きます。
以下、yukicoder様の解説と同様、答の値を $f(W,H)$ と書いていきます。「$f(W,H)$ が〇〇以上」という下からの評価については、その条件を満たす経路を具体的に構成するだけでよく、この部分に関してはyukicoder様の解説で完結しています。$f(W,H)$ の上からの評価に焦点を当てて論じていきます。
$H,W$ がどちらも偶数の場合
まずは次の図を見てみましょう。これは、yukicoder様の解説ページ の、$W = 10, H = 6$ の場合の図の移動経路です。頂点や辺に色を塗ったりしています。
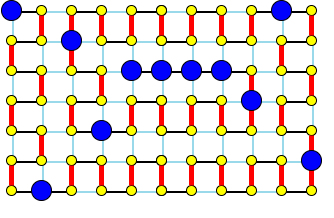
移動経路上の頂点をそれっぽい定義で「曲がる点」「直進点」の2種に分類することにします。また便宜上、スタートとゴールも直進点としておきます。上の図では、直進点を青頂点としています。また、移動経路上の縦線を、赤線として表しています。
以下のようにして、直進点の個数が $W + 1$ 以上であることが分かります:
- 赤線のみを辺とするグラフを考える。
- 縦に並ぶ $H+1$ 個の点を考える。 $H+1$ は奇数である。握手補題 などにより、このうち奇点は偶数個。よって偶点は奇数個ある。
- 特に、偶点は、縦に並ぶ $H+1$ 頂点の中に $1$ つ以上存在する。全体では $W+1$ 個以上。
- 偶点は必ず直進点(※スタートとゴールを除き同値)なので、直進点は $W+1$ 個以上。
ここまで分かれば、元の問題の最大値が、$(W+1)(H+1) – \max(W,H)$ 以上であることも容易です。曲がる点は$(W+1)(H+1) – (W+1)$ 以下であり、経路に含まれる線分の個数は、曲がる点の個数より $1$ 多いことから、\[f(W,H) \leqq (W+1)(H+1) – (W+1) + 1 = (W+1)(H+1) – W\] が得られます。$W,H$ を入れ替えて同様の議論を行うことで、$f(W,H) \leqq (W+1)(H+1) – H$ も分かるので、合わせて $f(W,H) \leqq (W+1)(H+1) – \max(W,H)$ が示されました。
$H = W$ の場合
$H = W$ については、あとひとつ評価を改良する必要があります。

経路の始点に注目します。必要ならば縦と横を入れ替えて、始点から縦線でスタートしているとしてよいです。あとは上と同じ議論をすればよいです。
- 赤線グラフにおける偶点は $W+1$ 個以上存在する。これらは全て直進点。
- 経路の始点は、「偶点ではない直進点」。したがって直進点は $W+2$ 個以上。
あとは同様にして、 $f(W,H) \leqq (W+1)(H+1) – W – 1$ が証明されます。
$H,W$ の片方が偶数, 片方が奇数の場合
$H$ が偶数であるとして、$f(W,H) \leqq (W+1)(H+1) – W$ を示しましょう。
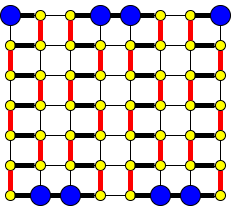
とはいったものの、この場合は、「$H,W$ ともに偶数の場合」と同様です。各縦列に直進点の存在がいえます。省略。
$H,W$ がどちらも奇数の場合
やはり、直進点の個数を下から評価することが課題です。
$(H,W) = (1,1)$の場合は容易なので省略します(一部適用できない議論があるため)。
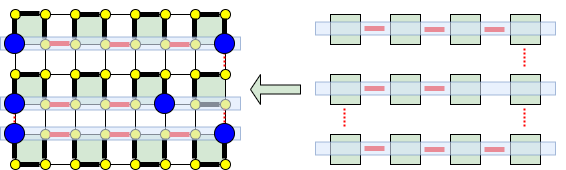
下の左図は、$H = 5$, $W = 7$ の場合の経路の具体例です。$H,W$ は奇数ですが、頂点は縦横に偶数個ずつ並びます。したがって、頂点を $2\times 2$ のグループに分けることができます。グループとなる4点を、緑色の正方形として図示しています。また、異なるグループ間の移動を赤線で表しています。(同グループ間の移動経路は、黒の太線で表しています)。
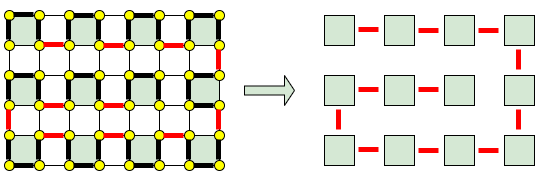
以下、$H+1 = 2a$, $W+1 = 2b$ として $a,b$ を定めます。 緑色の正方形は $a\times b$ の形に並んでいます。これら「緑色の正方形」を頂点、「赤線」を辺と見立てて、グラフを考えましょう。なお上図の場合には、単純パスの形をしていますが、一般には同じ頂点を複数回通る場合もあります。
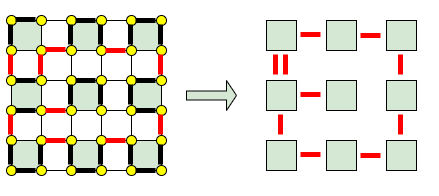
右側のグラフに対する次の補題を証明します。
【補題】$a, b$ を $ab\geqq 2$ であるような正の整数とする。頂点が $a\times b$ の長方形状に並んでいて、辺が隣接する頂点(4方向)にのみ貼られた連結グラフがあるとする。このとき、次のいずれかが成り立つ:
・全ての行に対して、少なくとも 1 つの辺が存在する。
・全ての列に対して、少なくとも 1 つの辺が存在する。
例えば 図4, 図5 の右側のグラフでは、いずれも全ての行に対して辺が存在します。
補題を証明しましょう。行に対する条件が成り立たない(反例となる行が存在する)と仮定して、列に対する条件を確認すればよいです。
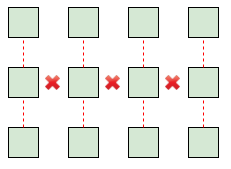
これは適当に図を描けば分かります。反例となる行をとります。その行に含まれる頂点が孤立点にならないようにするためには、上下のどちらかに辺が出ていなければいけません($ab\geqq 2$ かつ連結なので、孤立点はダメ)。この行の全ての頂点がそうなので、全ての列に辺が必要なことが示されました。
さて、緑正方形に対するグラフについて、全ての行に辺が存在するとしましょう。これを元の移動経路に戻すと、少なくとも $a$ 個の行に対して、赤線(正方形間の移動)が存在すると分かります。
そのような行に含まれる $2b$ 個の頂点に注目する。この行は、横方向に完全マッチングにならない。よって、横線のみを辺と見た場合に偶点が存在する。握手補題などにより偶数個の偶点が存在するので、この行には少なくとも $2$ 個の偶点(したがって直進点)が存在する。
(※ この辺の議論は、「 $H,W$ がどちらも偶数の場合 」で行った議論と同様です。縦線と横線が入れ替わってしまったので、そこに注意してください)
分かったこと:「$a$ 個以上の行にそれぞれ $2$ 個以上の直進点」が存在。
合計で、$2a = H+1$ 個以上の直進点の存在が分かりました。これは、補題における「全ての行に辺が存在」する場合の結論です。列側の場合も合わせると、$\min(H,W) + 1$ 個の直進点の存在が示されており、あとはこれまでと同様にして結論を得ます。
感想
出題ポリシーにはええっってなったけど、題材自体は楽しめました。
奇数の場合は、注目した値がなかなか機能せず、失敗の連続でかなり悩まされました。移動経路上の任意の点は $2$ つの辺に接続しますが、その局所的な性質だけでは絶対に上手くいかないです(緑色の正方形の辺集合が反例)。そこに気づいたことで、筋の良い方針を見分けられるようになりました。局所的な偶奇よりも、連結性に基づいた議論が必要だと断定できますので。
もう少しうまくできる余地はありそうですがいかがでしょう。
あとは、 draw.io に少し親しみました。

