遅延伝搬 Segment 木まで一通り、 $0$ から実装できるようことを目指して、丁寧に自習しました。折角なので記事化。
概要
を前提としています。
- 1点更新、区間作用、区間積取得が可能な Segment 木。
- いわゆる非再帰実装
- 1-based index
- $N=2^n$ を仮定しない
モノイド $A$ がモノイド $X$ に右作用するとします。各々のモノイドの二項演算を、積の形で、$$\begin{align*}A\times A\longrightarrow A;\quad (a,b)\mapsto ab,\\X\times X\longrightarrow X;\quad (x,y)\mapsto xy\end{align*}$$ と書きます。作用は、$$X\times A\longrightarrow X;\quad (x,a)\mapsto x^a$$ と指数の形で書くことにします。
- モノイド:結合法則 $(xy)z = x(yz), (ab)c = a(bc)$ が成り立つということ(単位元もある)。
- 右作用:$(xy)^a=x^ay^a$, $x^{ab} = (x^a)^b$ が成り立つということ(他に、単位元の作用が自明であることなどが仮定される)。
この記事ではモノイド、作用の具体例は扱いません。左作用($(ab)x = a(bx)$)でもよいのですが、そこはお好みでどうぞ。時系列順で後に行った作用を $A$ の演算で左右どちらにつけたいかです。
$x_i$ などと書いたらモノイド $X$ の元です。$a,b,c$ などは $A$ の元とします。$X$ の元の列 $[x_0,x_1,\ldots,x_{N-1}]$ が与えられたとき、
- $x_i$ の値を変更
- $x_L,\ldots,x_{R-1}$ を同時に $x_i^{a}$ に変更
- $\prod_{L\leq i < R} x_i$ の計算
が行える Segment 木を扱います。$x_1^ax_2^ax_3^ax_4^a = (x_1x_2x_3x_4)^a$ などが成り立つことを使って、区間積への作用をまとめて計算してあげることで、クエリあたり $O(\log N)$ 回の演算(モノイドの演算 or 作用)が実現されます。
作用が要素数や両端のインデックスに依存するものもありますが、それもこの枠組みで扱えます。例えば $X$ をモノイドとするとき、$Y = \N\times\N\times X$ として、$y_1=(L_1,R_1,x_1)$ と $y_2=(L_2,R_2,x_2)$ の積を $(L_1,R_2,x_1x_2)$ としたモノイド $X$ を考える(適当に単位元つけて)と、両端のインデックスを作用の定義に含めることができます。$R_1 = L_2$ じゃないときは未定義とすべき・モノイドではなく圏を扱っているという見方もありますが、気にせずいきます。
実装を観察しながら、特に具体値でのアルゴリズムを丁寧に可視化することで、$0$ からすぐに実装できるような盤石な理解を目指します。
参考文献
- data-structures / Lazy Segment Tree https://scrapbox.io/data-structures/Lazy_Segment_Tree
- 遅延伝搬 Segment 木でできる操作や計算量が簡潔にまとまっています。
- 遅延伝播セグメント木について https://beet-aizu.hatenablog.com/entry/2017/12/01/225955
- モノイド、作用の例など。
- Efficient and easy segment trees https://codeforces.com/blog/entry/18051
- 可換性が仮定されている。1-based, 非再帰。
- 遅延評価セグメント木をソラで書きたいあなたに http://tsutaj.hatenablog.com/entry/2017/03/30/224339
- 0-based, 可換, 再帰。
- 非再帰版の遅延評価セグメント木の実装メモ https://smijake3.hatenablog.com/entry/2018/11/03/100133
- 0-based, 可換, 非再帰。
- セグメント木の上に乗る構造はモノイドではなく圏である https://kimiyuki.net/blog/2018/12/06/categories-on-segment-tree/
- 記事タイトル通り
可視化
私の実装例:https://yukicoder.me/submissions/470340
まずは、$N = 8$ としてやっていきます。コードを載せる前に、 ひたすら何をするとどうなるべきかの可視化をしていきましょう(この辺、特に非可換だとあまり充実していなくて困った)。
区間作用
作用素の単位元は省略します。対象となる区間を $O(\log N)$ 個の区間に分割し、そこの作用素を追加する。というのはすぐに想像がつくと思います。これに加えて前処理と後処理が必要になり、次の $3$ ステップが必要です。
(1)作用素の伝搬
(2)作用素の追加
(3)再計算

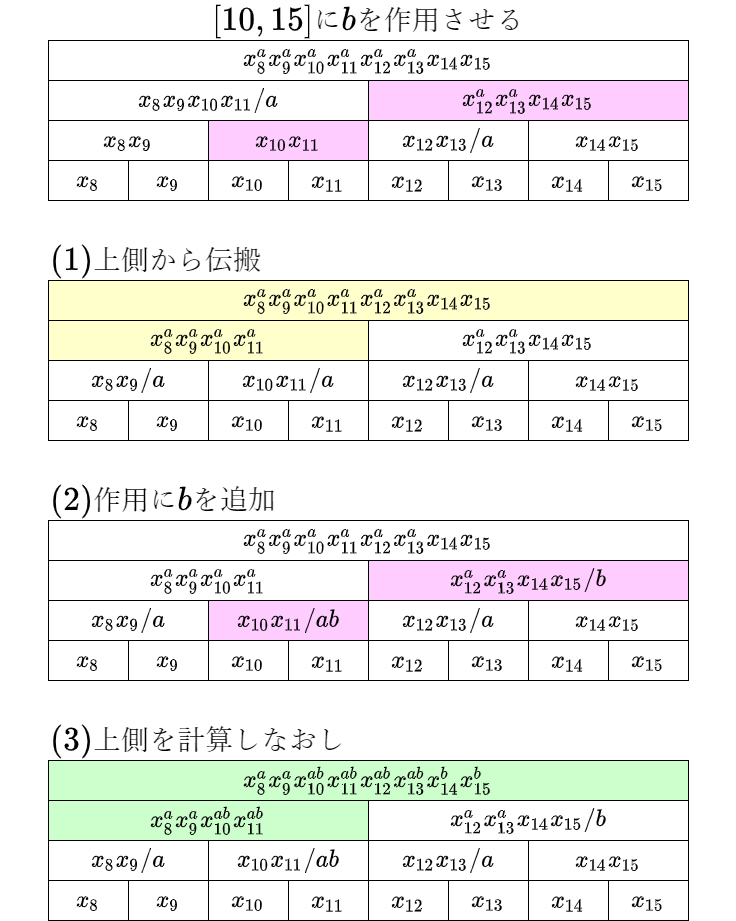
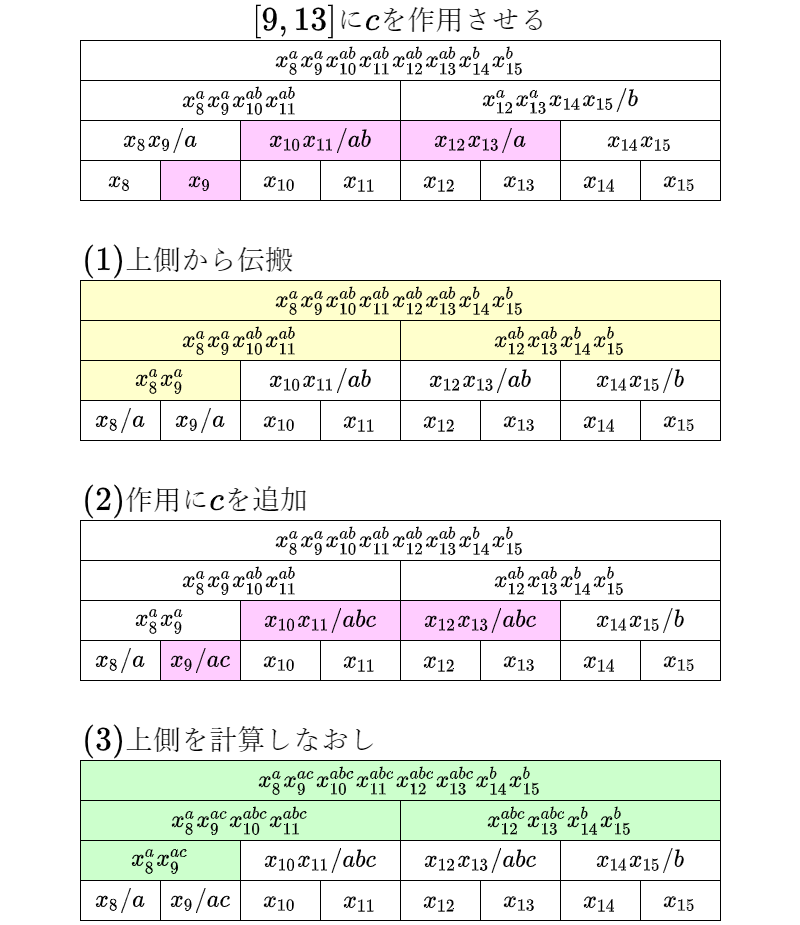
実際の挙動を図示してみるの、個人的には理解にとても良いと思っていて。実際これを見ただけでも自力実装できるような気がします。
セルのデータ $(x,a)$ は、だいたい対応する区間積が $x$ であること、作用素 $a$ が作用していることを意味しています。ただし、そのセルの上方にある作用素も含めて評価することで、初めて正しい値になるようになっています。上段ほど作用素の反映が終わっていて、下段ほど作用素の反映が遅れていることが観察できますね。上方ほど優先して反映を済ませるのはなぜかというと、
- あるセルの上方の情報を全てもらってくるのは簡単 ($O(\log N)$ 個)
- あるセルの下方の情報を全てもらってくるのは難しい($O(N)$ 個)
という違いがあります。下段のセルが最新の作用素を持てていないですが、これは必要になったときにすぐに 上からもらってこれます。一方、必要になってから慌てて下の情報をとってこようとしても、必要なものがどこにあるか分からないので、あるセルを更新したらその瞬間に上部に計算を反映させないといけないです(ステップ(3))。
ステップ(1)は、作用素が可換であれば必要にならないところです。作用が非可換であれば、作用の順序が迷子にならないように注意しなくてはいけません。そのため、作用を追加する区間の上部に作用素が残っていない状態に書き直してから、作用素を追加します。上にある作用素の方が下にある作用素よりも時系列順で後に追加されている状態がキープされます。
実装の確認は後にして、区間積の計算、$1$ 点更新の計算も先に可視化していきます。
区間積
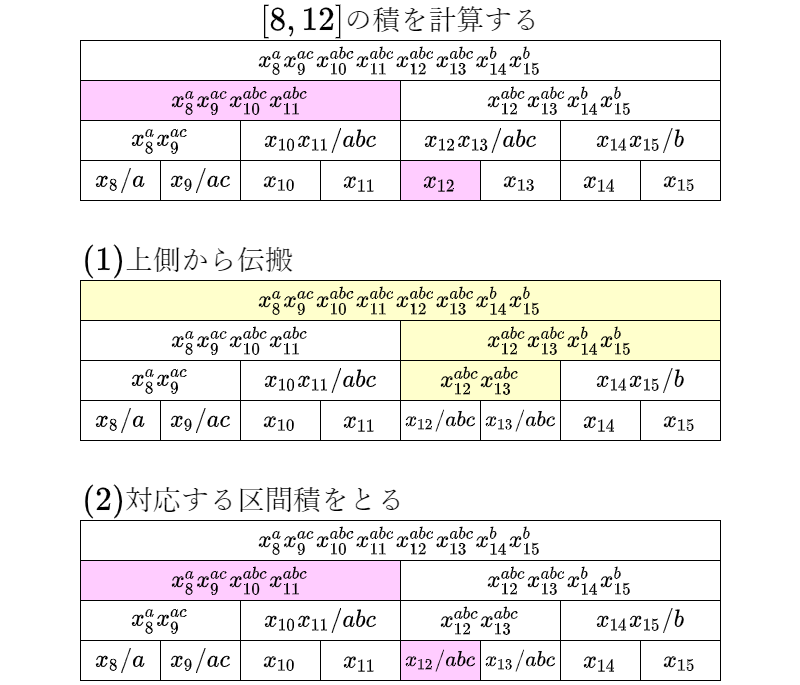
やるべきことは単純です。参照される区間に、上方の作用素を伝搬してきます。あとは普通の(遅延伝搬のない)Segment 木と同じです。上の例だと、積 $x_8^ax_9^{ac}x_{10}^{abc}x_{11}^{abc}x_{12}^{abc}$ が計算されます。
1点更新
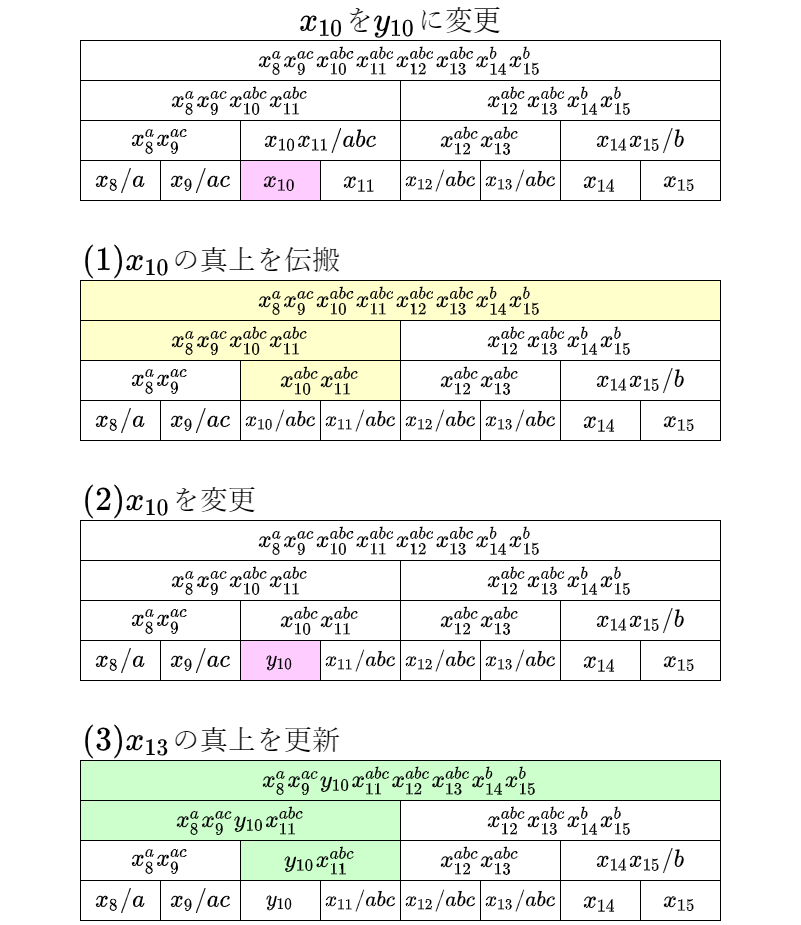
対象となる点を含む区間に残っている作用素を伝搬してしまえば、あとは下段から更新していくだけです。(1)において伝搬するときに $x_{10}^{abc}x_{11}^{abc}$ の部分を計算していますが、ここはどうせ再計算される部分なので、省略することもできます(実装が僅かに増える)。
伝搬させるインデックスの取得
- 区間作用 (1)(3)
- 区間積 (1)
ではそれぞれ、対象となるセルの真上にあるセル群に対して、作用素の伝搬または再計算を行う必要がありました。そのセル群が一体何者なのかが分かれば、実装の難所はおしまいです。
$N=40$, $L=45$, $R=78$ で可視化してみましょう。

作用素や積の計算対象がピンクのセル、伝搬や再計算をするのが黄色のセルです。
$N=2^n$ じゃない図なので、例によって一部に異常値が入ります。
計算対象となる区間たちの真上に並ぶ区間。なのですが、実際には「左端・右端の計算対象区間」の真上を見るだけで十分です。上の図の場合には、$45$ 番、$38$ 番のセルの真上です。
したがって、両端の計算対象区間を取得できればよいということになります。Segment 木の区間積の計算を思い出します。インデックスの遷移だけ見ると、こんな感じです。
while L < R:
if L & 1:
(セル L の値をかける)
L += 1
if R & 1:
R -= 1
(セル R の値をかける)
L >>= 1
R >>= 1特に、初めて計算対象になるまでの遷移を確認すると、きわめて単純です。$L$, $R$ とも、奇数になるまで $2$ で割り続けるだけです。
したがって、区間 $[L,R)$ に $a$ を作用するときには、例えば以下のようにすればよいです。
L0 = L // (L & -L) # 奇数になるまで L を 2 で割ったもの
R0 = R // (R & -R) # 奇数になるまで R を 2 で割ったもの
(L0 の真上を伝搬する)
(R0 の真上を伝搬する)
while L < R:
if L & 1:
(L に作用素 a を追加)
L += 1
if R & 1:
R -= 1
(R に作用素 a を追加)
L >>= 1
R >>= 1
(L0 の真上を再計算する)
(R0 の真上を再計算する)あるセルの真上に対して、伝搬:上から下の順、再計算:下から上の順に計算することに注意して実装すれば完成です。再計算は、いつものです。
while i > 1:
i >>= 1
(2i, 2i+1 での値を使って i の値を計算)伝搬は、上から下の順に行います。$i$ の $n$ 個上のセルが $\lfloor\frac{i}{2^n}\rfloor$ であることに注意すると、これも簡単なループです。
h = (2^h <= i となる h の最大値)
for n in range(h, 0, -1):
(i >> n における伝搬)
