遅延伝搬 Segment 木まで一通り、 $0$ から実装できるようことを目指して、丁寧に自習しました。折角なので記事化。
遅延伝搬 Segment 木は後日、別記事で。 → Segment Tree のお勉強 (2)
概要
- モノイドの列を扱う。1点更新、区間積取得が可能な Segment 木。
- いわゆる非再帰実装
- パフォーマンスを得る手段と思って学んでみたら、むしろこの方が分かりやすいと感じた。
- 1-based index
- $N=2^n$ を仮定しない
- 意外と文献が少なく、自分で図示するまで納得できなかったりした。
Segment 木は、文献は豊富なのですが、この辺の条件もばらばらだったり、微妙に分かりたいものが全部そろっていなかったりして(交換法則が前提となっていたり、実装の解説がなかったり、などなど)、 理解を深めるまでに文献をうろうろする必要があり、時間がかかりました。自分のためにも一度整理しておきます。
$x_i$ などと書いたらモノイド $X$ の元です。$X$ の元の列 $[x_0,x_1,\ldots,x_{N-1}]$ が与えられたとき、
- $x_i$ の値を変更
- $\prod_{L\leq i < R} x_i$ の計算
が行える Segment 木を扱います。実装を観察しながら、特に具体値でのアルゴリズムを丁寧に可視化することで、$0$ からすぐに実装できるような盤石な理解を目指します。
参考文献
- data-structures / Segment Tree https://scrapbox.io/data-structures/Segment_Tree
- Segment 木でできる操作や計算量が簡潔にまとまっています。
- beetさん セグメント木記事まとめ https://beet-aizu.hatenablog.com/entry/2019/11/27/125906
- モノイドの例など使用例が豊富。また記事ではないが、実装はbeet さんのものを参考にしました。
- Efficient and easy segment trees https://codeforces.com/blog/entry/18051
- 大体同じ実装方針。コードの説明は丁寧。交換法則が仮定されている部分が多いので注意。
- アリ本 p. 153
- 2べき, 再帰, 0-based
- セグメント木をソラで書きたいあなたに http://tsutaj.hatenablog.com/entry/2017/03/29/204841
- アリ本と同じ(多分)実装の詳しい解説
- 非再帰セグ木サイコー!一番すきなセグ木です https://hcpc-hokudai.github.io/archive/structure_segtree_001.pdf
- この記事と同方針。$N\neq 2^n$ の図もあり、二分探索も扱っています。
実装・可視化
私の実装例:https://judge.yosupo.jp/submission/7795
まずは、$N = 8$ としてやっていきます。
初期化
def build(self, seq):
for i, x in enumerate(seq, self.N):
self.X[i] = x
for i in range(self.N - 1, 0, -1):
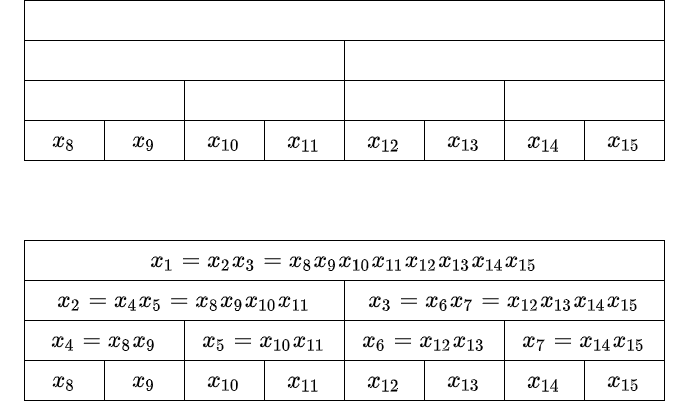
self.X[i] = self.X_f(self.X[i << 1], self.X[i << 1 | 1])実際のデータは、インデックス $[N, 2N)$ 部分に入れます。インデックス $i$ でのデータを $x_i$ とするとき、$x_i = x_{2i}x_{2i+1}$ が成り立つようにします。後ろから順に計算できます。
1点更新
def set_val(self, i, x):
i += self.N
self.X[i] = x
while i > 1:
i >>= 1
self.X[i] = self.X_f(self.X[i << 1], self.X[i << 1 | 1])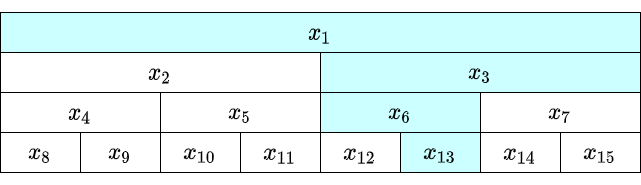
最下段のしかるべき場所を書き換えて、そのまま上に。ある要素を含む区間たちには、インデックスを $2$ で割っていくことで、遷移可能です。
区間取得
def fold(self, L, R):
L += self.N
R += self.N
vL = self.X_unit
vR = self.X_unit
while L < R:
if L & 1:
vL = self.X_f(vL, self.X[L])
L += 1
if R & 1:
R -= 1
vR = self.X_f(self.X[R], vR)
L >>= 1
R >>= 1
return self.X_f(vL, vR)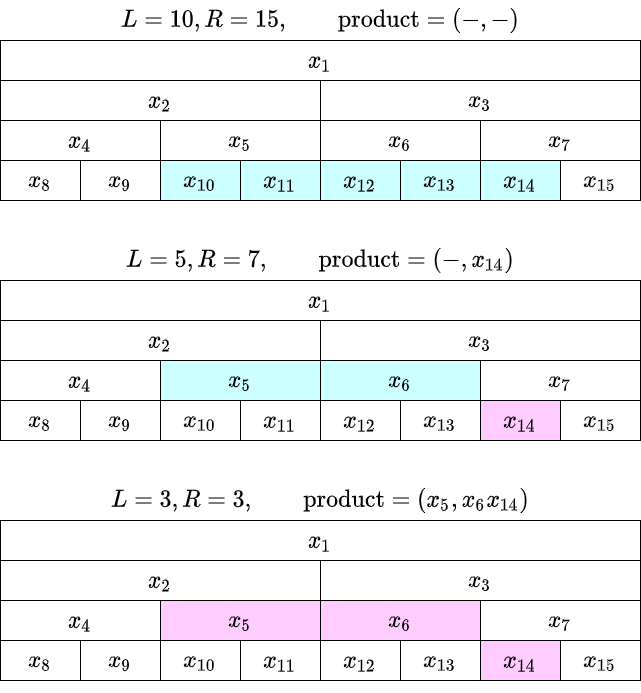
いわゆる非再帰実装では、外側から計算していきます。「左側の計算済の積、右側の計算済の積」に加えて、「未計算の区間、$x_L,\ldots,x_{R-1}$」を持ってループします。
$L$ が奇数だと、$x_L$ をその場で計算、$R-1$ が偶数だと $x_{R-1}$ をその場で計算。それ以外の部分は $2$ つずつの積がまとめて同じ親のところに入っているので、計算をひとつ上の段に委ねます。意識したことがなかったですが、最終的には左から奇数番号、右から偶数番号の $x_i$ が掛け算されるのですねー。
交換法則を仮定しない実装では、積の順序に注意しましょう。例えば上の例では、右側の積を $x_{14}x_6$ にしてしまわないように注意します。
交換法則を仮定するのであれば、左側・右側に分けて計算過程を持つ必要はなく、好きな順に好きな方向からどんどん計算結果に追加していけばよいです。
$N=2^n$ を仮定しない場合
実は全く同じコードで動きます。と初め聞いたときは、驚きました。例えば $N=11$ で図示してみます。

上の図で見たことがありますが、下の図の方が理解に適しているように感じます(個人差?)。
今までのように、$x_i = x_{2i}x_{2i+1}$ のルールで埋めていきます。全マス埋めるのですが、このとき、一部の $x_i$ には、区間積に対応しない、異常値が入ります($x_{5}=x_{20}x_{21}x_{11}$ など)。ですが、この値は計算に使われないので実は壊れないという仕組みです。

区間積の計算を思い出してみましょう。最下段から順に、孤立している両端は計算。$2$ つずつまとめられる区間は上の段に帰着する。というだけです。一部異常値が入っている場所が出来てしまうという話でしたが、 $2$ つずつまとめて正常な値が入っているところの上には正常な値が入っているので、区間積の計算は正常に機能します。
ところで
$x_1 = x_{16}x_{17}x_{18}x_{19}x_{20}x_{21}x_{11}x_{12}x_{13}x_{14}x_{15}$ となっていますね。
どんな $N$ でも、こんな感じで $x_1$ には全要素の積が入ります。ただし、積の順序が壊れているので異常値の類です。
しかし、可換モノイドという話であれば、$x_1$ は正常な全要素積になります。覚えておくと、しばしば使えるのではないでしょうか?

