グラフ数え上げ

概要
ラベル付き無向グラフ
ラベルなし無向グラフ
1. ラベルなし根付き木 $[0, 1, 1, 2, 4, 9, 20, 48, 115, \ldots]$
2. ラベルなし木 $[0, 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, \ldots]$
ラベル付き有向グラフ
参考文献

概要

「$N$ 頂点のグラフであって xx を満たすものはいくつありますか？」という種類の問題を扱います．

いわゆる入力定数個の数え上げ問題です．「グラフが与えられるので条件を満たす部分グラフを数えよ」というタイプの問題は扱いません．

特に，競技プログラミングでそのものまたは類似物が問われたことがあるものが中心です．導出方法が「グラフが与えられるので条件を満たす部分グラフを数えよ」というタイプの出題に応用できるものもあります．他にも重要な例があれば，随時追加するかもしれません．

なおグラフの辺の個数もパラメータとした数え上げ問題も考えられますが，これも本記事では扱いません．ただし多くの例では，紹介している手法をそのまま辺の個数も考える場合に一般化可能です．

本記事では次の用語を用います．

グラフについて，特に明記しない場合でも，単純グラフであることを仮定します．つまりループと多重辺がないものを扱います．
グラフが labeled であるとは，頂点集合が $\{0,1,\ldots,N-1\}$ であり，2 つのグラフは辺の有無が不一致であるような 2 頂点の組がある場合に区別して数えることといいます．
グラフが unlabeled であるとは，同型であるようなグラフを同一視して数えることをいいます．
グラフが連結であるとは，頂点集合が空集合ではなく，任意の 2 頂点に対してそれらを結ぶパスが存在することいいます（そうではない流儀もあるので注意してください）．

グラフの EGF （指数型母関数 / exponential generating function）をよく用います．ある性質を満たす $n$ 頂点のグラフが $a_n$ 個あるとき，その EGF とは $A(x) = \sum_{n=0}^{\infty}a_n\dfrac{x^n}{n!}$ のことをいいます．この記事では特に定義しなくとも，「EGF $A(x)=\sum_{n=0}^{\infty}a_n\dfrac{x^n}{n!}$」のように，EGF の文字と数え上げを表す数列の文字は同じアルファベットの大文字・小文字を用いることにします．

例えば「$n$ 頂点のグラフの EGF を $A(x)$ とする」と書けば，$n$ 頂点のグラフの個数を $a_n$，$A(x)=\sum_{n=0}^{\infty}a_n\dfrac{x^n}{n!}$ であるということとします．

ラベル付き無向グラフ

ラベル付き無向グラフ $[1, 1, 2, 8, 64, 1024, \ldots]$

特に条件をつけない場合，頂点数 $N$ のラベル付き無向グラフの個数は $2^{\binom{N}{2}}$ です．すべての $2$ 頂点間に辺を作るか否かを定めるためです．

OEIS：https://oeis.org/A006125
実装例：https://maspypy.github.io/library/graph/count/count_labeled_undirected.hpp

ラベル付き無向連結グラフ $[0, 1, 1, 4, 38, 728, \ldots]$

ラベル付き無向グラフの EGF を $A(x)$ とし，ラベル付き無向連結グラフの EGF を $B(x)$ とします．このとき，$A(x) = \exp B(x)$ が成り立ちます．

典型的な $\exp$ の利用法です．簡単に理由を確認しておきます．

$a_{n,k}$ を，連結成分がちょうど $k$ 個であり，各連結成分に $0, 1, \ldots, k-1$ のラベルがついているものの数え上げとします．$a_n = \sum_{k=0}^{\infty}\dfrac{a_{n,k}}{k!}$ です．連結成分につけたラベルを忘れたあとすべての $k$ について和をとることを考えればこうなります．

$a_{n,k}$ を求めましょう．ラベル $i$ の連結成分の大きさが $n_i$ とすると，$a_{n,k}=\sum_{n_0+\cdots+n_{k-1}=n}$ というタイプの和に分解できます．足すものは，まず頂点集合を各ラベルの成分に分割する多項係数 $\dfrac{n!}{n_0!\cdots n_{k-1}!}$ がつきます．さらに，各頂点集合を連結グラフにするための方法の数 $\prod b_{n_i}$ がつきます．結局，

$$a_{n,k}=\sum_{n_0+\cdots+n_{k-1}=n}\frac{n!}{n_0!\cdots n_{k-1}!}b_{n_0}\cdots b_{n_{k-1}}$$

となります．したがって，$\sum_{n=0}^{\infty}a_{n,k}\dfrac{x^n}{n!}=B(x)^k$ です．

これらを $\dfrac{1}{k!}$ 倍して足し合わせて，$A(x)=\sum_{k=0}^{\infty}\dfrac{B(x)^k}{k!}=\exp B(x)$ となります．

計算したいものは $B(x)$ で，$A(x)$ は既に求めたものです．よって $B(x)=\log A(x)$ により答が計算できます．

OEIS：https://oeis.org/A001187
実装例：https://maspypy.github.io/library/graph/count/count_labeled_connected.hpp

ラベル付き木 $[0, 1, 1, 3, 16, 125, \ldots]$

$N=0$ ならば $0$ 個，$N>0$ ならば $N^{N-2}$ 個です．Cayley の公式と呼ばれています．

OEIS：https://oeis.org/A000272 （$N=0$ の場合の値が $1$ となっています，空グラフを木と定義する流儀があるのかかなり疑問ですが．）
実装例：https://maspypy.github.io/library/graph/count/count_labeled_tree.hpp

非常に多くの証明が知られています．形式的べき級数の扱いに慣れているならば，ラグランジュ反転を用いる証明が簡潔だと思います．ラベル付き根付き木の個数が $N^{N-1}$ であることを示しましょう．ラベル付き根付き木の EGF を $A(x)$ とすると，ラベル付き根付き木から根を除けば再びラベル付き根付き木に分解されることを考慮すれば，$A(x)=x \exp A(x)$ が得られます．これをラグランジュ反転すれば $a_n=n^{n-1}$ が得られます．

ラベル付き森 $[1, 1, 2, 7, 38,291, \ldots]$

ラベル付き木の EGF を $A(x)$，ラベル付き森の EGF を $B(x)$ とすれば，$B(x)=\exp A(x)$ が成り立ち，$b_n$ が計算できます．

OEIS：https://oeis.org/A001858
実装例：https://maspypy.github.io/library/graph/count/count_labeled_forest.hpp

ラベル付き $N$ 辺 $N$ 頂点連結グラフ $[0,0,0,1,15,222, \ldots]$

$N$ 辺 $N$ 頂点連結グラフは唯一サイクルを持つ連結グラフというのと同値で，unicyclic graph などの名称があります．日本語競プロ界隈だと，なもりグラフという俗称もあります．

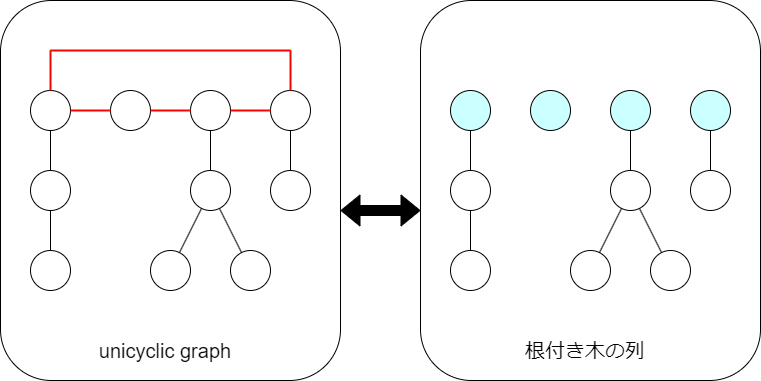
唯一のサイクル上に適当に始点と向きを付けてから切ると，根付き木の列が得られます．

そこで unicyclic graph の EGF を $A(x)$，根付き木の EGF を $B(x)$ とすれば，サイクルの頂点数が $k$ （$k\geq 3$）であるような unicyclic graph の EGF は $\dfrac{1}{2k}A(x)^k$ となり，$A(x)=\dfrac12\sum_{k=3}^{\infty}\dfrac{1}{k}B(x)^k$ となります．

和の範囲が $k\geq 3$ であることに注意すると，右辺は $\dfrac12 \log (1-B(x))-\dfrac12 B(x)-\dfrac14B(x)^2$ であることが分かり，これで $A(x)$ が計算できます．EGF の合成に慣れている場合には，単にサイクルの EGF と根付き木の EGF の合成であるという理解もできるでしょう．

OEIS：https://oeis.org/A057500
実装例：https://maspypy.github.io/library/graph/count/count_labeled_unicyclic.hpp

ラベル付き無向連結オイラーグラフ $[0, 1, 0, 1, 3, 38, 720, \ldots]$

連結かつすべての頂点の次数が偶数であるようなグラフを数えましょう．

例によって，連結性の条件を外して「すべての頂点の次数が偶数」であるようなグラフを数えたあと，$\log$ をとればよいです．

「すべての頂点の次数が偶数」であるようなグラフは，全域木をひとつとれば，全域木に含まれないすべての辺に対して結ぶか結ばないかを決めることと対応するため，$2^{\binom{n-1}{2}}$ 個あります．

OEIS：https://oeis.org/A033678
実装例：https://maspypy.github.io/library/graph/count/count_labeled_eulerian.hpp

ラベル付き無向連結 2 部グラフ $[0,1,1,3,19,195,\ldots]$

2 部グラフとは，頂点全体を 2 つの独立集合に分割可能であるようなグラフです．分割が可能だというだけで，分割の方法には任意性があることに注意します．そこで次の定義をします．

色付き 2 部グラフとは，グラフ $G$ および，その各頂点を色 $0$, $1$ で塗る方法の組であって，辺で結ばれた点の色が異なるもののことをいう．

色付き 2 部グラフの EGF を $A(x)$，連結色付き 2 部グラフの EGF を $B(x)$，連結 2 部グラフの EGF を $C(x)$ とすると，$A(x)=\exp B(x)$ および $B(x)=2C(x)$ が分かります．後者については連結 2 部グラフを 2 彩色する方法がちょうど 2 通りあることから分かります．

よって $C(x)=\dfrac12 \log A(x)$ なので，$A(x)$ が計算できればよいです．色 $0$ の頂点 $n_0$ 個，色 $1$ の頂点 $n_1$ 個の場合を考えることで

$$a_n=\sum_{n_0+n_1=n}\dfrac{n!}{n_0!n_1!}2^{\binom{n}{2}-\binom{n_0}{2}-\binom{n_1}{2}}$$

より $\dfrac{a_n}{n!2^{\binom{n}{2}}}$ が畳み込みで書けて， $A(x)$ が計算できます．

OEIS：https://oeis.org/A001832
実装例： https://maspypy.github.io/library/graph/count/count_labeled_bipartite.hpp

ラベル付き無向 2 部グラフ $[1, 1, 2, 7, 41, 376, \ldots]$

ラベル付き無向連結 2 部グラフの EGF を $\exp$ すれば，ラベル付き無向 2 部グラフの EGF が得られます．上と同じ記号を用いれば，求めるものは $\exp C(x)$ ということになります．

$C(x)=\dfrac12 \log A(x)$ なのでした．したがって $\exp C(x)=\sqrt{A(x)}$ となるので，$\exp, \log$ の計算は不要で sqrt をとるだけになります．

OEIS：https://oeis.org/A047864
実装例：https://maspypy.github.io/library/graph/count/count_labeled_bipartite.hpp

ラベル付き 2 重辺連結グラフ $[0, 1, 0, 1, 10, 253, \ldots]$

この記事では，橋のない連結グラフを 2 重辺連結グラフと呼ぶことにします．英語 wikipedia における定義とは整合していると思いますが，後述の OEIS では $N=1$ に対する値が $0$ となっているため，$N=1$ の場合には複数の流儀があるかもしれません．

導出過程で現れる EGF 各種を定義します．

$A(x)$ を 2 重辺連結グラフの EGF とします．
$B(x)$ を根付き 2 重辺連結グラフの EGF とします（根付きグラフとはグラフとその 1 点の組のことで，明らかに $b_n=na_n$ です）．
$C(x)$ を連結グラフの EGF とします．
$D(x)$ を根付き連結グラフの EGF とします．
$E(x)$ を根付き連結グラフであって，根に接続する辺がすべて橋であるものとします．

明らかに，$b_n=na_n$ および $d_n=nc_n$ が成り立ちます．

$D(x)=B(E(x))$ が成り立つというのが面白い議論です．このことを確認しましょう．とりあえず図を見てください．

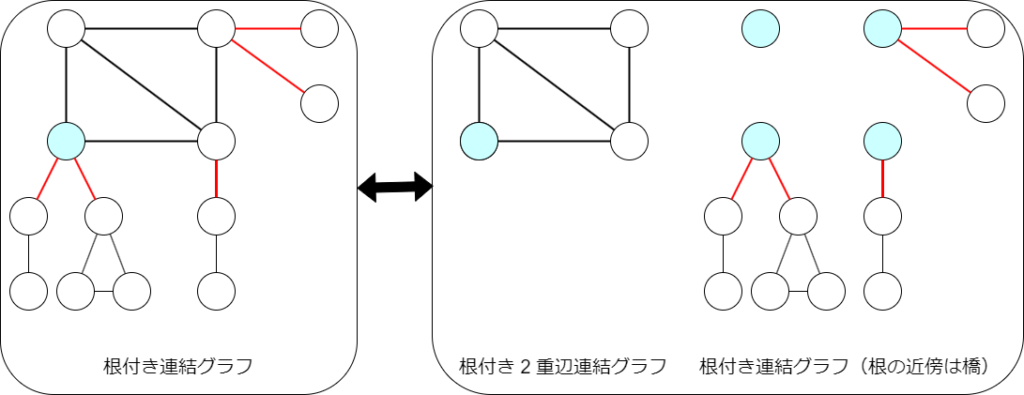
根付き連結グラフがあるとき，根を含む 2 重辺連結成分を取り出すことで，根付き 2 重辺連結グラフが定まります．さらに，成分内の各頂点に接続する橋および橋の反対側を集めてくると，成分内の各頂点に対して，根に接続する辺がすべて橋であるような根付き連結グラフがひとつずつ定まります．この対応を丁寧に見ると $D(x)=B(E(x))$ という式が得られます．ラベルの有無など混乱要素が多いと思うので，丁寧に見ていきましょう．

$d_n$ のうちで，根の 2 重辺連結成分の大きさが $k$ であるものの個数を $d_{n,k}$ とします．$k$ を固定して，$\sum_{n=0}^{\infty}d_{n,k}\dfrac{x^n}{n!}=b_k\dfrac{E(x)^k}{k!}$ を示せばよいです．$k!$ 倍した式 $\sum_{n=0}^{\infty}k!d_{n,k}\dfrac{x^n}{n!}=b_k E(x)^k$ を示しましょう．

$k!d_{n,k}$ は，ラベル付き根付き連結グラフの根の 2 重辺連結成分に対してさらにラベル $0, 1, \ldots, k-1$ を割り当てたものを考えることに対応します．これは上の図の分解によって

$k$ 頂点からなるラベル付き根付き 2 重辺連結グラフ
番号 $0, 1, \ldots, k-1$ の根付き連結グラフ（根の近傍は橋）の組であって，全体として頂点ラベル $0, 1, \ldots, n-1$ がついているもの

の組に対応します．ラベル付きグラフにラベルが付いているという感じのややこしい状況なので慎重に考えてみてください．

各番号の根付き連結グラフの頂点数 $n_i$ を固定することで，後者の数え上げは多項係数 $\dfrac{n!}{n_0!\cdots n_{k-1}!}$ と $e_{n_0}\cdots e_{n_{k-1}}$ の積になり，$n_i$ を動かすとこれは $[x^n]n!E(x)^k$ と書けることが分かります．以上をまとめると $D(x)=B(E(x))$ が得られます．

あとは $E(x)$ が求まると良さそうです．また，$E(x)=x \exp D(x)$ が成り立ちます．これは，$E(x)$ で対象となっているグラフの根を取り除くと，根付き連結グラフに分解されることから分かります．

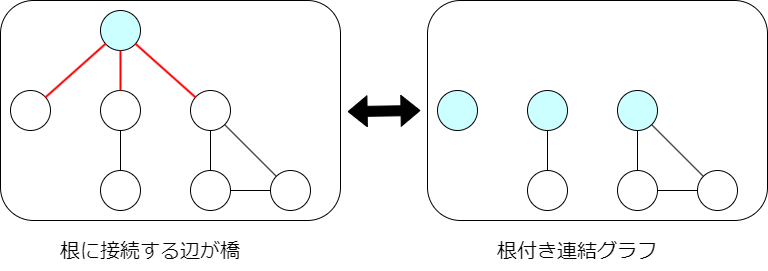
画像に alt 属性が指定されていません。ファイル名: bridgeless_1.drawio-1.png

目標は $A(x)$ の計算です．$A, B$ の間には簡単な関係があるので，$B(x)$ を計算すればよいです．$C(x)$ は既に計算されており，したがって $D(x)$ も簡単に計算できます．$E(x)$ は $E(x)=x\exp D(x)$ により計算できます．

結局，$D(x)=B(E(x))$ という状況で $D(x), E(x)$ が与えられているときに $B(x)$ を求めればよいです．これは，$E(x)$ の合成に関する逆元を $D(x)$ に代入すれば計算できます（$B, D, E$ は $0$ 次の係数が $0$ です）．

OEIS：https://oeis.org/A095983
実装例：https://maspypy.github.io/library/graph/count/count_labeled_bridgeless.hpp

$b_N$ （したがって $a_N$）を得るだけならば，ラグランジュ反転による $\Theta(N\log N)$ 時間での計算も可能です（上の実装例に，このタイプの実装もあります）．

ラベル付き 2 重連結グラフ $[0,0,1,1,10,238,\ldots]$

根付きのグラフを考えることもあれば，根なしのグラフにおいて頂点 $0$ を特別視して議論することもあるので，これらの混同に注意してください．

結果的に添字をひとつずらしておくと綺麗になる，という意味の微分が発生します．

$A(x)$：2 重連結グラフの EGF．
$B(x)=A'(x)$：$b_n=a_{n+1}$ という列の EGF．
$C(x)$：連結グラフの EGF．
$D(x)=C'(x)$：$d_n=c_{n+1}$ という列の EGF．
$E(x)$：根付き連結グラフの EGF．
$F(x)$：$2$ 頂点以上で頂点 $0$ が関節点でないような連結グラフの EGF．
$G(x)=F'(x)$：$g_n=f_{n+1}$ という列の EGF．

2 重辺連結成分のときと違って，頂点 $0$ を含む 2 重連結成分をとろうとしても，それは一意ではないのでやりにくいです．一方で，頂点 $0$ が関節点ではないという条件を付けると 2 重辺連結成分の場合と似た議論が可能になって，今回は $G(x)=B(E(x))$ という式を得ることができます．

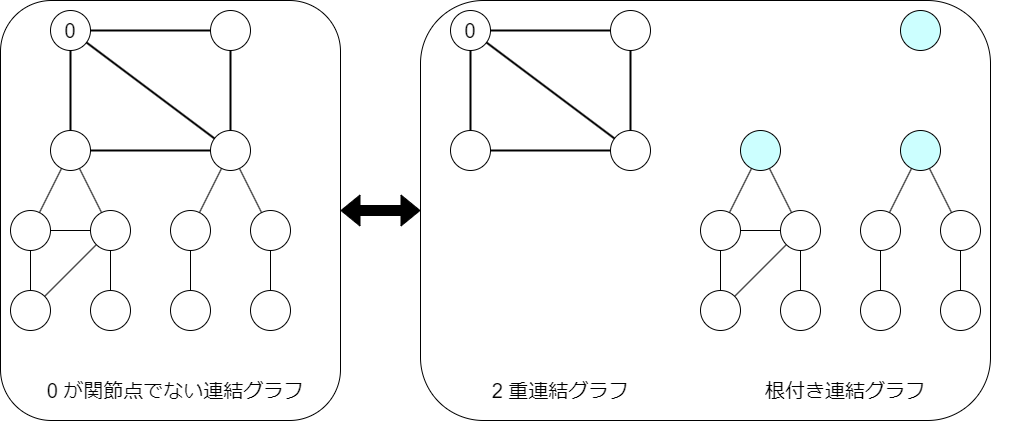
議論は 2 重辺連結の場合と同じです．ラベル $0$ の頂点を特別視しているので，ラベル $1, 2, \ldots, n-1$ を $k-1$ 個の成分に分配するという形になって，添字を $1$ ずらしている（$A(x)$ の代わりに $B(x)=A'(x)$，$F(x)$ の代わりに $G(x)=F'(x)$ を考えている）おかげでシンプルな合成の関係式が得られています．

あとは，「頂点 $0$ が関節点ではない」というグラフの数え上げを考えればよいです．

任意の連結グラフを考えて，頂点 $0$ を除いたときの連結成分分解を考えます．

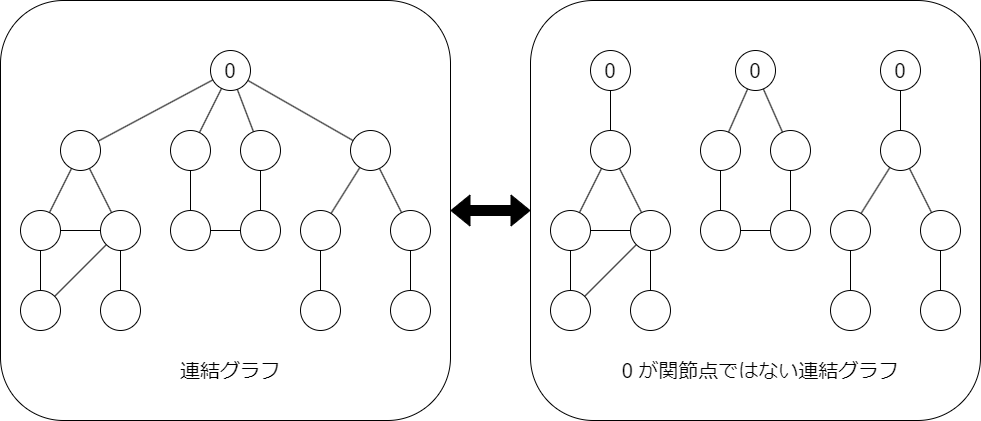
すると，$D(x)=\exp G(x)$ という関係式が得られます．

結局，計算手順は以下の通りです．まず $C(x)$ を求めます．すると $D(x), E(x)$ が求まります．

$D(x)=\exp G(x)$ より $G(x)$ が求まります．$E, G$ が求まったので， $G(x)=B(E(x))$ から $B(x)$ が求まります．したがって $A(x)$ が求まります．

OEIS：https://oeis.org/A013922
実装例：https://maspypy.github.io/library/graph/count/count_labeled_biconnected.hpp

ラベルなし無向グラフ

同型なグラフを同一視する必要があり，一般的にはこちらの方が難易度が高いと思われます．

ラベルなし根付き木 $[0, 1, 1, 2, 4, 9, 20, 48, 115, \ldots]$

$A(x)$ をラベルなし根付き木の OGF とします．つまり，$a_n$ をラベルなし根付き木の個数とし，$A(x)=\sum_{n=0}^{\infty} a_nx^n$ とします．

ラベルなし根付き木は根を取り除くことで，根付き木の multiset と対応します．したがって，ラベルなし根付き木を得るには，より小さなラベルなし根付き木それぞれを何個使うかを定めればよいです．このことから，

$$A(x)/x = \prod_{n=1}^{\infty}(1+x^n+x^{2n}+\cdots)^{a_n}$$

が得られます．頂点数 $n$ のラベルなし根付き木を使う回数を選ぶ部分が $(1+x^n+x^{2n}+\cdots)$ に対応し，そのような木が $a_n$ 個あるため $a_n$ 乗がかかります．両辺の対数をとると $\log (A(x)/x) = \sum_{n=1}^{\infty}-a_n\log(1-x^n)$ なので

$$A(x)/x = \exp\biggl(\sum_{n=1}^{\infty}-a_n\log(1-x^n)\biggr)$$

が得られます．この式から，あとは Relaxed Convolution のテクニックを使えば，$a_0, a_1,\ldots,a_n$ を既知としたときに $a_{n+1}$ を計算できます．結局，$a_0,\ldots,a_N$ の列挙を $\Theta(N\log^2N)$ 時間で行うことができます．

OEIS：https://oeis.org/A000081
根付き木：https://maspypy.github.io/library/graph/count/count_unlabeled_tree.hpp

ラベルなし木 $[0, 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, \ldots]$

つい最近，Shirotsume さんが解説しました．

ここでは少し違った導出を紹介しましょう（ https://users.math.msu.edu/users/magyarp/math482/Otter-Trees.pdf に基づく，dyssymmetry theorem と呼ばれることがある手法を利用します）．

$a_n$ を木の個数とします．
$b_n$ を木とその頂点の組（つまり根付き木）の個数とします．
$c_n$ を木とその辺の組の個数とします．
$d_n$ を木とその辺とその向きの組の個数とします．

いずれも数え上げはラベルなし木としての数え上げで，同型による同一視を行います．根や向きがついたものについても，それを保つ同型による同一視を行います．

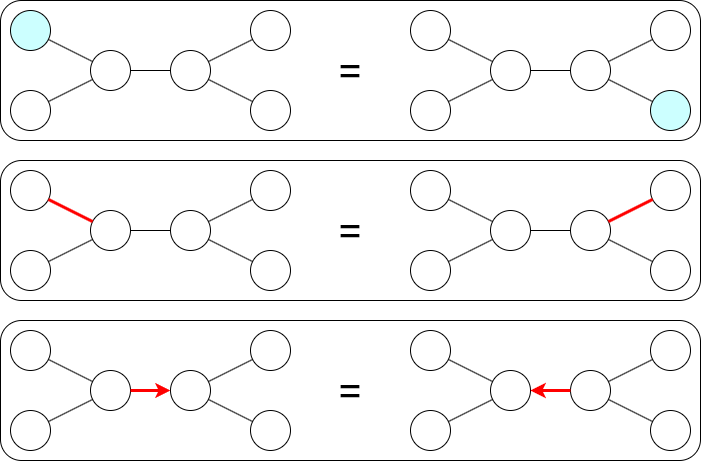
基本的には $d_n=2c_n$ になりそうですが，選ばれている辺が木の中心であるときにはどちらの向き付けも同じと見なされることに注意してください．

次が成り立ちます：$a_n=b_n+c_n-d_n$．

以下では木の元論文などに合わせて木の中心を用いた議論をしますが，木の重心を用いても同じ議論が可能です．

木は唯一の中心（これは 1 点または 1 辺）を持つことを考えれば，$b_n+c_n-a_n$ は次の数え上げと一致することが分かります：

木と，頂点または辺の組であって，選んだ頂点または辺が中心と不一致であるものの個数．

これが $d_n$ と一致することを確認しましょう．

選んだ頂点が中心ではない頂点であるとき，その頂点から中心に向かう方向に辺とその向きを選ぶことにします．選んだ辺が中心ではない辺であるとき，その辺を中心から遠ざかる方向に向き付けます．すると，全ての辺とその向きの組が一度ずつ登場して $b_n+c_n-a_n=d_n$ が示されます．

中心である辺の向き付けも，頂点から中心に向かう形でちょうど 1 回登場することに注意してください．

$a_n, b_n, c_n, d_n$ の OGF を $A(x), B(x), C(x), D(x)$ とします．

$B(x)$ は既に計算しました．
選んだ辺をグラフから削除することを考えると，$c_n$ 2 つの木からなる非順序対の数え上げと等しいです．ここから，$C(x)=\dfrac{1}{2}(B(x)^2+B(x^2))$ が分かります．
選んだ辺をグラフから削除することを考えると，$d_n$ 2 つの木からなる順序対の数え上げと等しいです．ここから，$D(x)=B(x)^2$ が分かります．

したがって $A(x)=B(x)+\dfrac12 (B(x)^2-B(x^2))$ が分かります．

OEIS：https://oeis.org/A000055
実装例：https://maspypy.github.io/library/graph/count/count_unlabeled_tree.hpp

ラベル付き有向グラフ

ラベル付き有向グラフ $[1,1,4,64,4096,\ldots]$

$n$ 頂点ラベル付き有向グラフの個数を $a_n$ とすると，$a_n=2^{n(n-1)}$ が成り立ちます．

グラフにはループ・多重辺がないとしていますが，反対方向に向き付けられた辺が両立する場合は考えています．

ラベル付きDAG $[1,1,3,25,543,\ldots]$

有向グラフにおける入次数 $0$ の点を source といいます．

$a_n$ を $n$ 頂点のラベル付き DAG の個数とします．
$b_n$ を $n$ 頂点のラベル付き DAG であって，source が $0$ 個のものの個数とします．

source が $0$ 個の DAG なんてものは空グラフ以外に存在しないので，当然 $B(x)=1$ です．この EGF を別の方法で計算しましょう．

包除原理を考えます．source になるという条件を指定した $k$ 個の頂点がある場合の数え上げを考えて，$(-1)^k$ 重みで足せばよいです．

source とする $k$ 頂点の間には辺がなく，それ以外の $n-k$ 頂点の間では DAG を作り，これらの間 $k(n-k)$ 辺には source からの辺を自由に作れることなどから，

$$b_n=\sum_{k=0}^n\binom{n}{k}(-1)^ka_{n-k}2^{\binom{n}{2}-\binom{k}{2}-\binom{n-k}{2}}$$

という式が出てきます．

これは畳み込みの形で書けます．$b_n$ を既知として $a_n$ は，係数に適切な $2$ べきをつけながら形式的べき級数逆元の計算を一度行うというタイプの計算で求めることができます．

OEIS：https://oeis.org/A003024
実装例：https://maspypy.github.io/library/graph/count/count_labeled_dag.hpp

ラベル付き強連結グラフ $[0,1,1,18,1606,\ldots]$

有向グラフの強連結成分のうちで，他の連結成分から入る辺が存在しないものを，source strong component といいます．

$a_n$ を $n$ 頂点のラベル付き有向グラフの個数とします．
$b_n$ を $n$ 頂点のラベル付き有向グラフで，source strong component が $0$ 個のものの個数とします．
$c_n$ を $n$ 頂点のラベル付き強連結有向グラフの個数とします．

今回も $B(x)=1$ です．これを別の方法で計算しましょう．

包除原理を考えます．source strong component になるという条件を指定した $k$ 個の部分集合がある場合の数え上げを考えて，$(-1)^k$ 重みで足せばよいです．まず次の $d_n$ を定義します．

$d_n$ を $n$ 頂点のラベル付き有向グラフであって，すべての強連結成分が source strong component であるようなものの個数．ただし，強連結成分が $k$ 個である場合に $(-1)^k$ の重みをつけて数える．

すると，$D(x)=\sum_{k=0}^{\infty}(-1)^k\frac{C(x)^k}{k!}=\exp(-C(x))$ です．また，DAG のときと同様に

$$b_n=\sum_{k=0}^n\binom{n}{k}d_ka_{n-k}2^{\binom{n}{2}-\binom{k}{2}-\binom{n-k}{2}}$$

という関係式も得られます．$A(x)$, $B(x)$ が既知であることから $D(x)$ が計算でき，これの $\log$ をとることで $C(x)$ が計算できます．

OEIS：https://oeis.org/A003030
実装例：https://maspypy.github.io/library/graph/count/count_labeled_strong_digraph.hpp

ラベル付きトーナメント $[1,1,2,8,64,1024,\ldots]$

トーナメントとは，任意の 2 頂点対に対してちょうど 1 つの有向辺があるようなグラフです．

それぞれの辺の向きが 2 通りありうるため，$2^{\binom{N}{2}}$ 個のトーナメントがあります．

ラベル付き強連結トーナメント $[0,1,0,2,24,544,\ldots]$

ラベル付きトーナメントの EGF を $A(x)$ とします．
ラベル付き強連結トーナメントの EGF を $B(x)$ とします．

トーナメントの強連結成分分解を考えます．一般に強連結成分をまとめて 1 つの頂点として扱うと，DAG が得られますが，トーナメントの場合にはトーナメントかつ DAG であるようなグラフが得られます．したがって，$k$ 個の強連結成分に全順序が定まり，強連結成分の間にはその順序に従って辺が張られるということが分かります．

結局，ラベル付きトーナメントを得るには，頂点全体を $k$ 個の部分集合に分割し，それらに適当な順序を定め，それぞれの部分集合内にラベル付き強連結トーナメントを定めればよいです．このことから，$A(x)=\sum_{k=0}^{\infty}B(x)^k=\dfrac{1}{1-B(x)}$ が得られます．

$A(x)$ は既知なのでこれで $B(x)$ が計算できます．