問題概要
問題文 → ■, ■
自分の提出 → ■(根付き木, 169 ms),■ (全方位,332 ms)
Static Top Tree (以下 STT)と呼ばれるデータ構造を用いた解法の実装例について解説します.
STT は競技プログラミングでの流行は比較的最近ですが,このことは実装や理解の難しさを表すわけではありません.どちらかというと,実装の簡潔さと応用の強力さを兼ね備えているところが優れていて,木のデータ構造の中でも習得しやすい方だと思います.
とは言ったものの新しさゆえに資料が少なく,また実装の自由度が高いため,誰もが使っているような標準的な実装が分かりにくいといった学習の難しさがあります.
私の実装もあまり良い感じではないかもしれませんが,とりあえず現時点で Fastest付近 / Fastest がとれていることと,そもそも全方位版での実装例や解説がほとんど存在しないように思ったので,何かしらの役に立つかもしれないと思って記事を書きます.
Static Top Tree 参考文献
- https://atcoder.jp/contests/abc351/editorial/9868 (Nyaan さん)
- https://atcoder.jp/contests/abc351/editorial/9910 (yosupo さん)
- 関連 https://www.mathenachia.blog/mergetech-and-logn/ (Nachia さん)
- https://www2.ioi-jp.org/camp/2024/2024-sp-tasks/contest3/joitour-review.pdf (tatyam さん)
以下,これらを「Nyaan 解説」「yosupo 解説」「Nachia 解説」「tatyam 解説」などと引用します.
STT 初学者の方に真っ先に見て欲しい文献は,Nyaan 解説です.STT がとは何であるかが,かなり分かりやすく丁寧に書かれているので熟読することをお勧めします.
STT の構築には,rake, compress の順序や heavy path の選択などの自由度がありますが,yosupo 解説は線形時間の計算でその選択を(木の高さの意味で)最適化できることを示しており,理論的にも重要な結果であるように思います.私は HLD にまで手を入れるのは面倒に感じたのでそこは採用しませんでしたが, compress の実装の部分を参考にしました.作られる STT の木の高さについては,Nachia 解説で定数倍も含めて詳細に評価されています.
tatyam 解説は,根が virtual であるような半開区間 Path だけをクラスタとすることにより実装を簡潔にする(例えば Path, Point の区別を必要としない)方法が説明されています.light edge のマージなど,Point クラスタとして扱えるところも Path クラスタとして扱うために,余分なデータを持ってしまい,定数倍について最適な実装ではないと思うのですが,これを使っていて他の人の提出より実行速度で劣るという経験は今のところないので,この方法を採用しています.
解法(根付き木)
根が virtual であるような半開パスだけをクラスタとして,STT を構築します(tatyam 解説の方針).
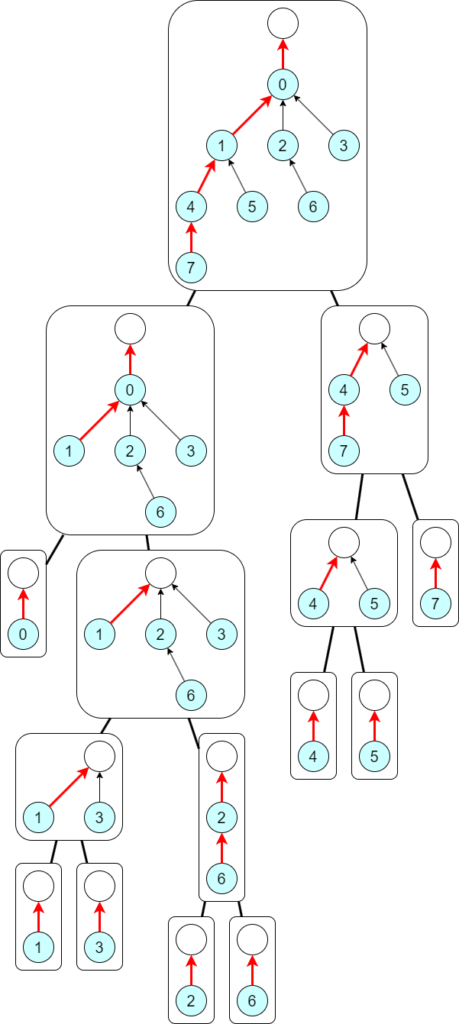
各 STT のノード(クラスタ)は,ひとつのパスが選ばれた(expose された)有向木です.
根付き木全体に virtual な根をひとつ追加します.STT の葉が元の木の頂点と対応するようになり,STT は頂点集合のマージ過程とも見なせるようになって個人的にも分かりやすかったので採用しています.
辺 $N-1$ 個のマージ過程として構築することも出来て,この方が “Static Top Tree” という呼称に合っているかもしれません($N=1$ の場合の対処に注意してください).また Nyaan 解説に沿って,辺と頂点を合わせた合計 $2N-1$ 個のもののマージ過程として構築することもできます.
構築手順は,HLD を使って再帰的に行えます.各頂点の light child 方向の部分木に関するクラスタを構築し,heavy child と rake でまとめたあと,heavy path に沿って compress します.
rake でまとめる部分は,貪欲に小さいもの 2 つをマージするという戦略.compress でまとめる部分は,部分木頂点数が半分になるあたりで分割統治すればオーダー最適になります(Nachia 解説).compress でまとめる部分についてはさらに,スタックを用いた簡単なアルゴリズムで「最適化」できることが yosupo 解説で示されており,私の実装でも採用しました.
ところで,私はつい最近まで,compress を heavy path の中央で分割するという,最悪計算量オーダーの悪化する方法で実装してしまっていましたが,実行速度のロスは小さいようです.HLD のパスクエリでの $\log$ を減らす工夫(■, ■)が通常の制約で大きな速度差がつきにくいのと似ていると思います.
STT が構築できたら,各クラスタに対して適当なデータを持たせて,クラスタに対するデータがボトムアップな木 DP で計算できるようにすれば,本問題の解法になります.
問題で与えられる木がパスの場合をセグメント木で解くとして,各半開区間に対してどのようなデータを持つべきかを考えると,考えやすいと思います.
各クラスタについてパス $[d,u)$ が expose されているとき,
- クラスタ内の頂点を根にうつしたときの値の総和,および頂点の個数
- パス $du$ 上の 1 次変換すべての合成
を持てばよいです.
- 解答例(169 ms)
全方位
各クラスタに対して,expose されているパスを逆向きにした場合のデータも持たせるようにします.
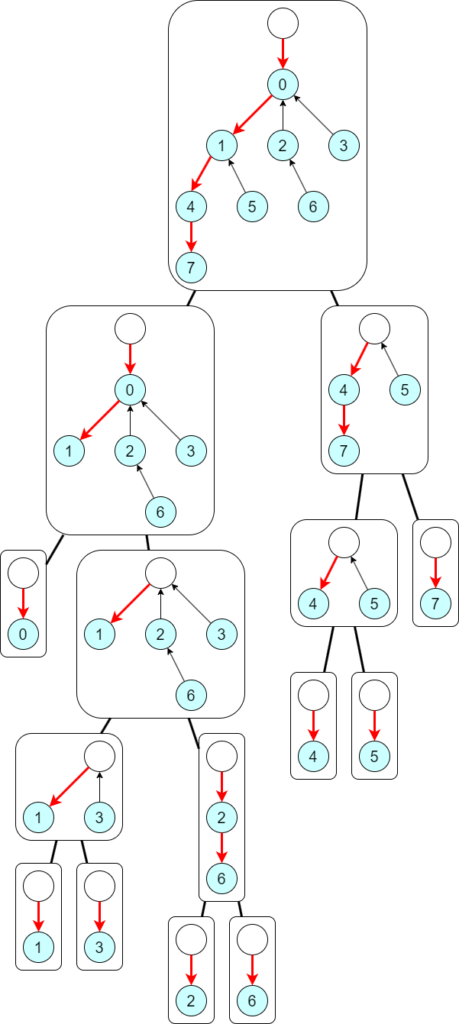
各ノードに,パスの向き 2 通りに対応する 2 つの集約値を持たせます.
virtual な点が expose されているパスの始点・終点であるようなデータを両方扱う必要がありますが,この混在はどのような実装方針でも避けるのは困難だと思います.(例えば 1 つの辺からなるクラスタについて子側を virtual であるような「逆向きのデータ」を持たせようとすると,頂点更新の計算量が壊れます).
この木DPが計算できるためには,次のようなクラスタのマージを実装できればよいです.
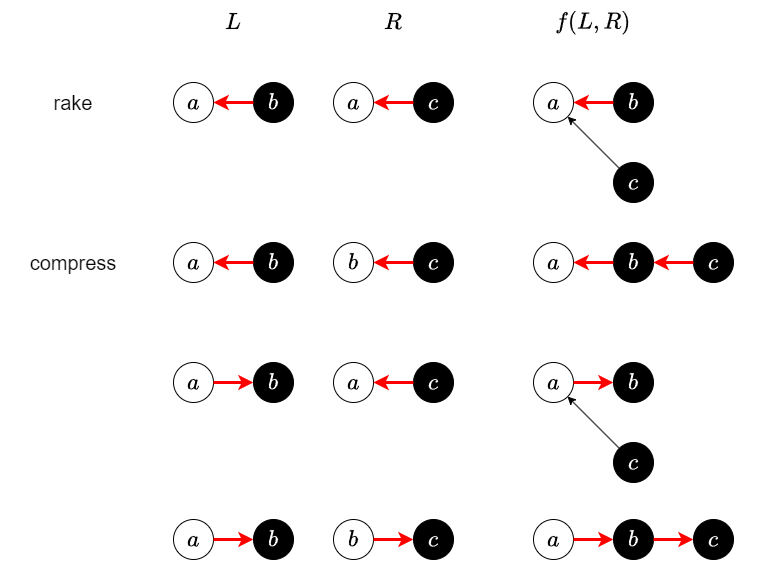
これらを実装すれば,STT の各ノードのクラスタに対応するデータが動的に更新できるようになります.
あとはこれに基づいて任意頂点を根とする有向木の集約値を得ましょう.
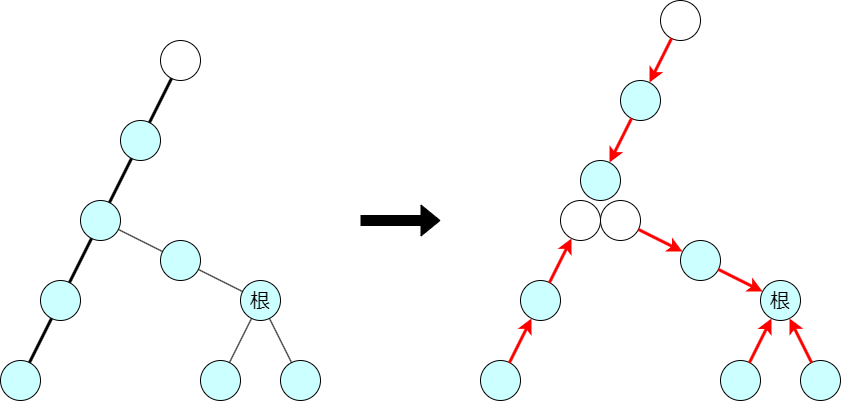
根にしたい点 $r$ を含むクラスタについて,パスとの位置関係に注目して,上のように $r$ 方向に根を持つ $3$ つの有向木を作って管理することにします.
STT の葉 $r$ からボトムアップにこれら $3$ つのデータを計算していけば完成です.最終的には,元の木の根の隣に virtual な点が expose されているような根付き木が完成します.
- 解答例(332 ms)
その他の方法について
少し書いておきますが,別解というよりは同じ解の実装方針の違いという感じになる気がします.
動的木の利用
根を変更する操作を持つ機能のある動的木で適切に実装すれば解けます.例えば Link Cut Tree で解けます.
Link Cut Tree の各ノードも,あるパスが expose された有向木(クラスタ)と見なすことが出来る(light edge も含めて LCT における subtree 全体を考えればよい)ため,light edge に対する集約値を適切に管理すれば各クラスタに対するデータを計算できます.今回は light edge に対する集約は sum であり,引き算が可能な分少し簡単になると思います.
light edge の情報も適切に管理する Link Cut Tree は,Top Tree とほとんど同じと言われていて,もちろん Top Tree でも本問が解けます.STT は,これら動的木の機能を静的な木に限定する代わりに実装を大きく簡略化したものだと考えられます.(私は Top Tree を実装したことがないのでこの辺は参考程度で.)
- ei1333 さんの実装例 (Link Cut Tree, 1362ms)
HLD の利用
ボトムアップに木DPを計算することを考え,heavy path 上での dp value の変換をセグメント木で管理します.これは light edge の集約から定まるため,点更新が入るたびにその頂点から根までのパスに沿って,light edge の値とセグメント木の点更新を交互に行っていきます.
heavy path を葉方向に下る際の dp value の変換もセグメント木で管理すれば,全方位のクエリにも答えられます.
light edge をひとつ更新した場合に light edge に対する集約値を更新する必要がありますが,本問では足し引きで更新できます.STT は,この更新にセグメント木のような二分木を利用したものとほとんど同じで,tute さんによる STT の実装ではよりこのことが強調されていると思います.

