個人的に勉強したことを整理します。
新規性とか強い主張とかは、特にありません。
Euler Tour
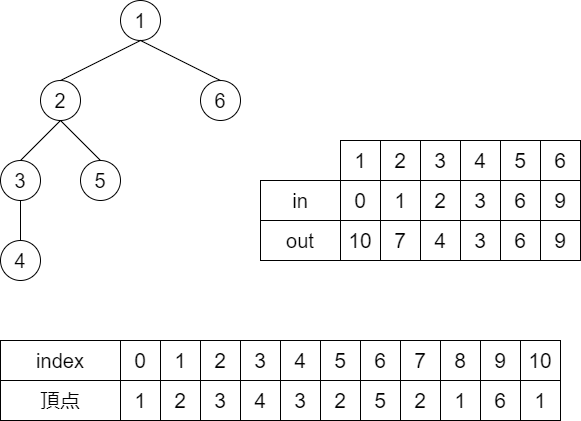
(1) DFS 順に探索して、通った頂点の列を記録する($1,2,3,4,3,2,5,2,1,6,1$)。
(2) 各頂点 $i$ について、最初に通った時刻と最後に通った時刻 $\mathrm{in}[i]$, $\mathrm{out}[i]$ を覚える。
参考:
・アリ本 p. 294 (Euler Tour の名前は出ていませんが)Euler Tour による LCA の計算。
登場する頂点を並べますが、計算で必要になるのはむしろ、$\mathrm{in}[i]$, $\mathrm{out}[i]$ の方ですね。例えば閉区間 $[\mathrm{in}[i], \mathrm{out}[i]]$ を見ると、$i$ を根とする部分木 $\mathrm{subtree}_i$ の頂点が分かるという特徴があります。木に対する主要な計算のいくつかを、区間に対する計算へと言い換えることができるようになりますね。

通った辺を並べてみる
アリ本の解説と同様、「通った頂点を順に並べます」というのが Euler Tour の基本だと思っていました。ブログ記事を検索しても、この説明の方が多いように思います(ただし探すと、以下に述べる、辺を基礎とした解説も複数存在しました)。 頂点 $i$ の根側の辺を $i$ として、辺に番号をつけます。上から下に通ったときに $+i$, 下から上に通ったときに $-i$ を並べましょう。
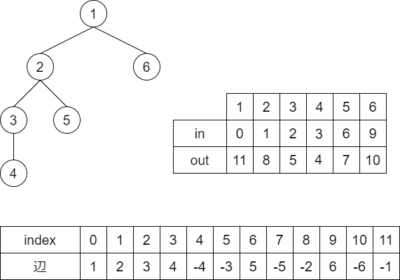
辺 $1, -1$ は実際には存在しないのですが、「今から探索始めるぞ!」「探索終わりました!」という「移動」に対応しているつもりで追加します。$\pm v$ がちょうど $1$ 回ずつ記録され、それが $\mathrm{in}[i]$, $\mathrm{out}[i]$ です。
※ 頂点を並べる説明でも同一の in, out のテーブルが作られるため、特に新しいことをやっている・新しいものが計算できるというわけではないです。
ただ個人的に、こちらの方が分かりやすいなと感じました。
まず、綺麗です。全ての辺が双方向に $1$ 回ずつ現れます。 部分木の範囲が見やすくて、部分木を表す区間同士が、完全な包含 or 交わらないことも個人的には意識しやすくなりました。$\mathrm{in}[i], \mathrm{out}[i]$ の間には部分木の辺が $2$ 回ずつ現れることから、部分木の辺の個数が $\frac12(\mathrm{out}[i]-\mathrm{in}[i]-1)$ になることも見やすいです(頂点数はそれよりも $+1$)。また例えば次の事実も、辺を並べようとするまで意識したことがなかったです。
「通った辺を並べたもの」から「通った頂点を並べたもの」を復元するのは簡単で、各辺の終点を対応させると変換できます(辺 $+i$ には頂点 $i$、辺 $-i$ には頂点 $\mathrm{parent}[i]$)。逆は少し手間です(in, out を見る、手前・後ろの頂点を見るなどが必要)。ので、「通った頂点を全て並べた列」には利点があまりないのかな?ということを考えていました。
クエリ各種
部分木クエリ
全ての頂点(辺)が値を持っているとします。頂点 $i$ の値を $v_i$、辺 $i$ の値を $e_i$ とします(可換モノイドに値を持つと仮定します)。
頂点 $i$ を根とする部分木に対し、その和の計算ができます。 同じ頂点を $2$ 回計算しないように、下向きの辺に対してのみ値を持たせます。

例えば空欄を単位元として Segment 木 を使えば、値の 1点変更・部分木取得ができます。同じことですが、遅延伝搬 Segment 木 を使えば、部分木更新にも対応できるでしょう。群であれば累積和あるいは Fenwick Tree で置き換えることも可能かもしれません。
見れば分かるように、このように index を持つと、配列の半分しか使いません。「下向きの辺に対してのみ値を持たせます」と言ったばかりでしたから、下向きの移動だけ使って配列を小さくすることができます。beet さんの記事では、頂点属性の Euler Tour と呼び分けています。私は不勉強ゆえ、実装したことがなかったです。
パスクエリ
根からある頂点 $i$ までのパスを考えたとき、このパスにおける頂点・辺の値の和を取得できます。

各時点で、累積和と計算対象が一致するようにします。群に値を持つ(逆元がとれる)場合にこれが可能です。可換性は要求しません。親 → 子 順の和が手に入ります(適切にやれば 子 → 親 順もできる)。
LCA
アリ本にあるので有名だと思いますが、これが最も発想しにくい Euler Tour の利用方法な気がします。

「両方の頂点を含む極小な部分木」と思うといまいちで、「$i$ から $j$ に DFS 順で移動するときに通る、最も根に近い頂点」というすごい言い換えをすると、区間最小値の計算に帰着されます。上の例だと、辺 $-2$ の終点として、$\mathrm{LCA}(3,6) = 1$ が計算できます。
ただし以下を見たときには、「両方の頂点を含む極小な部分木」 という見方も知っておくと役に立つなあと感じました。
「全ての頂点を含む部分木」は、「全ての頂点を含む区間」と言い換えられるので、 「$n$ 点の LCA」を求めるときに、左端と右端のものだけを見ればよくなります。$n$ 個の max や min をとったあとで $2$ 点の LCA を計算をすると、$n$ 点の LCA が計算できます。


