Dirichlet 積と、数論関数の累積和

2021.03.29

スポンサーリンク

Dirichlet 級数と Dirichlet 積

$\N = \{1,2,3,\ldots\}$ を定義域とする関数 $a, b\colon \N\longrightarrow \C$ を、数論関数　(arithmetic function) と呼ぶことがあります。

$c(n) = \sum_{ij=n}a(i)b(j)$ により定まる $c\colon \N\longrightarrow \C$ を、$a, b$ の Dirichlet 積といいます。この記事では、$c = a * b$ と表すことにします。この積は、交換法則・結合法則・分配法則などを満たします。

モノイド $(\N, \times)$ に関する畳み込み演算と言ってもよいです。$(\N\cup\{0\}, +)$ の畳み込み演算は、形式的べき級数に置き換えることで性質が見やすく整理できることがありますが、$(\N, \times)$ の場合には、Dirichlet 級数で表すことが一般的です。つまり、数列 $\{a_n\}$ を

$$D_a(s) = \sum_{n=1}^{\infty} a_nn^{-s}$$

に置き換えることで、$c = a * b \iff D_c = D_aD_b$ と Dirichlet 積は級数の積に変換されます。

  • $i^{-s}\cdot j^{-s} = (ij)^{-s}$ を、分配法則を満たすように拡張することで積を定義します。
  • $\text{Re}(s)$ が十分大きな複素数 $s$ の代入を考える場合もありますが、今回は収束などの細かいことは無視しましょう
  • 「$-s$」の符号は、歴史的な背景によりこうなっていますが、この記事では大事ではありません。式を書くのが手間であれば、全て「$+s$」にしてしまっても不都合は生じないでしょう。

また、無限数列を使って定式化をしますが、そのうち $1\leq n\leq N$ 部分だけを配列として持つのが基本的な取り扱いとなるでしょう。

Dirichlet 積の計算量

$a$, $b$ が既知で、$c = a*b$ のとき、$c(1), \ldots, c(N)$ を計算することは、$O(N\log N)$ 時間で行えます。次の要領です。

c = [0] * (N+1)
for i in range(1, N+1):
  for j in range(1, N//i+1):
    c[i*j] += a[i] * b[j]

乗法的 Dirichlet 級数の場合

$a(1) = 1$ かつ、互いに素な $n,m$ に対して $a(nm) = a(n)a(m)$ が成り立つような $a$ は、乗法的であるといいます。素べきでの値 $a(p^k)$ からすべての $a(n)$ が復元できるという性質で、約数の個数や和、Euler関数などの例が有名でしょう。

Dirichlet 級数の言葉で書けば、級数が Euler 積分解 $$D_a(s) = \prod_p \Bigl(\sum_{k}a(p^k)p^{-ks}\Bigr)$$ を持つことと対応します。

$O(N\log\log N)$ 時間での計算

$a$ が乗法的であるとき、$a*b$ の計算は $O(N\log\log N)$ 時間 で行えます。$a$ が疎な関数の Euler 積に分解されていることを利用して、in-place に $p$ パートの乗算を繰り返します。Dirichlet 積の言葉で書けば、

for p in primes:
  D_{a,p}(s) = sum a(p^k) p^{-ks}  (p-part of D_a)
  D_b(s) ← D_b(s) D_{a,p}(s)

といった計算をしていけばよいです。

c = b
for p in primes:
  for i in range(N//p, 0, -1):
    n = p * i
    # n = (p^k) * m となるとき、c[n] ← c[n] + a[p^k] * c[m] として更新
    q, m = p, i
    while True:
      c[n] += a[q] * c[m]
      if m % p != 0:
        break
      q, m = q * p, m // p

in-place に更新するため、更新順に注意しましょう。大きい番号から更新することで、後の計算に必要な部分が先に上書きされてしまうことを避けています。計算量は、$$\sum_{q=p^k\leq N}\Bigl\lfloor\frac{N}{q}\Bigr\rfloor=\sum_{p\leq N} \Bigl\lfloor\frac{N}{p}\Bigr\rfloor + O(N) = O(N\log\log N)$$ などと解析されます（$q$ は素数べきで、$p$ は素数）。

$O(N)$ 時間での計算

$c$ が乗法的ならば（特に $a, b$ が乗法的ならば）、$n$ が素数 $p$ でちょうど $k$ 回割り切れ $n = p^km$ と書けるとき、$c(n) = c(p^k)c(m)$ が成り立ちます。このことを利用すると、$c(1), \ldots, c(N)$ を $O(N)$ 時間で計算することもできます。

  1. 素数べき $p^k\leq N$ に対して、$c(p^k)$ を愚直に（$O(k^2)$ 時間で）計算する。
  2. $n = 2, 3, 4, \ldots$ の順に、それが素数べきでないならば、$n = p^km$ として $c(n) = c(p^k)c(m)$ により $c(n)$ を求める。

前計算として、各 $n$ を割り切る $p^k$ を持っておくことが必要になります。この前計算も、線形篩を用いることで $O(N)$ 時間で行うことが可能です。

Dirichlet 積と累積和

数論関数 $a$ に対して、$A(n) = \sum_{i=1}^n a(i)$ と書くことにします。この記事では小文字と大文字を対応させて、$a$ の累積和を $A$、$b$ の累積和を $B$、$c$ の累積和を $C$ で表すことにします。

まず、次を確認しましょう。

【命題 1】$c = a*b$ とし、任意の $1\leq i\leq N$ に対して $a(i), b(i), A(i), B(i)$ が計算されているとする。$C(N)$ は $O(\sqrt{N})$ 時間で計算できる。

$$C(N) = \sum_{n=1}^N \sum_{ij=n}a(i)b(j) = \sum_{ij\leq N}a(i)b(j)$$ と式変形をします。さらに、$M = \lfloor \sqrt{N}\rfloor$ として、$\sum_{i,j} = \sum_{i\leq M} + \sum_{i > M}$ と変形します。

  • $i \leq M$ を固定します。$ij\leq N\iff j\leq \lfloor N/i\rfloor$ なので、この部分は $a(i)B(\lfloor N/i\rfloor)$ と計算できます。
  • $i > M$ であるとき、$j \leq M$ である必要があります。$j$ を固定したとき、$i$ の範囲は $M < i \leq \lfloor N/j\rfloor$ なので、$b(j)\bigl(A(\lfloor N/j\rfloor) – A(M)\bigr)$ が固定した $j$ の寄与になります。

これらを足し合わせることで、$C(N)$ は $O(\sqrt{N})$ 時間で計算できました。

$N$ が大きいとき、この計算において、必要な $a(i), b(i), A(i), B(i)$ のインデックスはかなり疎 (sparse) です。再び $M = \lfloor \sqrt{N}\rfloor$ とおきます。

【命題 2】$c = a*b$ とし、次の形のものがすべて計算されているとする。

  • $1\leq i\leq M$ となる $i$ に対する $a(i), b(i)$
  • $1\leq i\leq M$ となる $i$ に対する $A(\lfloor N/i\rfloor)$, $B(\lfloor N/i\rfloor)$

このとき、$C(N)$ は $O(\sqrt{N})$ 時間で計算できる。

計算方法は全く同じです。さらに同じようにすると、次も分かります。

【命題 3】$c = a*b$ とし、次の形のものがすべて計算されているとする。

  • $1\leq i\leq M$ となる $i$ に対する $a(i), b(i)$
  • $1\leq i\leq M$ となる $i$ に対する $A(\lfloor N/i\rfloor)$, $B(\lfloor N/i\rfloor)$

このとき、次のものすべてが、合計 $O(N^{3/4})$ 時間で計算できる。

  • $1\leq i\leq M$ となる $i$ に対する $c(i)$
  • $1\leq i\leq M$ となる $i$ に対する $C(\lfloor N/i\rfloor)$

計算する前後でデータの持ち方をそろえることで、同様の計算の反復に備えています。アルゴリズムはほとんど変わりません。

$n = \lfloor N/i\rfloor$ と書ける $n$ に対して、$A(\lfloor n/j\rfloor)$ といった値が必要になりますが、$\lfloor n/j\rfloor = \lfloor N/ij\rfloor$ が成り立つため、結局計算のいたる所で $\lfloor N/i\rfloor$ と書けるようなインデックスしか登場しません。$A(1), \ldots, A(M)$ の値は新たに必要となりますが、これは $a(i)$ の累積和として簡単に手に入ります。

計算量を確認しましょう。

  • $c(1), \ldots, c(M)$ の計算に、$O(M\log M) = O(N^{1/2}\log N)$ 時間
  • 各 $C(\lfloor N/i\rfloor)$ の計算に、$i$ ごとに $O(\sqrt{N/i})$ 時間

となりますが、$\int_{1}^M\frac{1}{\sqrt{t}}dt = O(\sqrt{M})$ であることなどから評価すると、合計で $O(N^{3/4})$ 時間であることが分かります。

$\sqrt{n}$ で区切るという発想で自然に $O(N^{3/4})$ という計算量が出てきましたが、実はこの計算量は簡単に落とすことができます。

【命題 4】$N\leq KL$ となるように $K, L$ をとる。$c = a*b$ とし、次の形のものがすべて計算されているとする。

  • $1\leq i\leq K$ となる $i$ に対する $a(i), b(i)$
  • $1\leq i\leq L$ となる $i$ に対する $A(\lfloor N/i\rfloor)$, $B(\lfloor N/i\rfloor)$

このとき、次のものすべてが、合計 $O(K\log K + (NL)^{1/2})$ 時間で計算できる。

  • $1\leq i\leq K$ となる $i$ に対する $c(i)$
  • $1\leq i\leq L$ となる $i$ に対する $C(\lfloor N/i\rfloor)$

特に $K = \lceil (N/\log N)^{2/3}\rceil$, $L = \lceil N^{1/3}(\log N)^{2/3}\rceil$ ととった場合には、$O(N^{2/3}(\log N)^{1/3})$ 時間である。

また、この時間計算量は、以下の条件のように削減可能である。

  • $a, b$ のうち一方が乗法的であれば、$O(N^{2/3}(\log \log N)^{1/3})$ 時間
  • $a, b$ の両方が乗法的であれば、$O(N^{2/3})$ 時間

$C(N)$ ひとつ計算する場合には $N^{1/2}$ で切るのがオーダー最適でしたが、多くの値をまとめて計算する場合には、$N^{2/3}$ 程度で切ることでオーダーが改善できることになります。

アルゴリズムは同様で、

  • $c(1), \ldots, c(K)$ を、$O(K\log K)$ 時間で計算する。
  • $A(1), \ldots, A(K)$ および $B(1), \ldots, B(K)$ を $O(K)$ 時間で計算する。
  • 各 $1\leq i\leq L$ に対して、$C(\lfloor N/i\rfloor)$ を、$i$ ごとに $O(\sqrt{N/i})$ 時間で計算する（【命題 2】）。$1\leq i\leq L$ に対する合計時間は $O((NL)^{1/2})$ 時間である。

となって、$O(K\log K + (NL)^{1/2})$ 時間であることが分かります。

また $a, b$ がともに乗法的であれば、Dirichlet 積の計算がより高速に行えて、上記の計算が全体で $O(K + (NL)^{1/2})$ 時間であることも分かります。この場合には $K = \lceil N^{2/3}\rceil$, $L = \lceil N^{1/3}\rceil$ ととれば、$O(N^{2/3})$ 時間が実現できますね。

除算の計算

同じ議論をうまく遡ることで、次の操作も行えることが分かります。$a_1\neq 0$ が必要になります。

【命題 5】$N\leq KL$ となるように $K, L$ をとる。$a*b = c$ とし、次の形のものがすべて計算されているとする。

  • $1\leq i\leq K$ となる $i$ に対する $a(i), c(i)$
  • $1\leq i\leq L$ となる $i$ に対する $A(\lfloor N/i\rfloor)$, $C(\lfloor N/i\rfloor)$

このとき、次のものすべてが、合計 $O(K\log K + (NL)^{1/2})$ 時間で計算できる。

  • $1\leq i\leq K$ となる $i$ に対する $b(i)$
  • $1\leq i\leq L$ となる $i$ に対する $B(\lfloor N/i\rfloor)$

特に $K = \lceil (N/\log N)^{2/3}\rceil$, $L = \lceil N^{1/3}(\log N)^{2/3}\rceil$ ととった場合には、$O(N^{2/3}(\log N)^{1/3})$ 時間である。

また、この時間計算量は、以下の条件のように削減可能である。

  • $a, c$ のうち一方が乗法的であれば、$O(N^{2/3}(\log \log N)^{1/3})$ 時間
  • $a, c$ の両方が乗法的であれば、$O(N^{2/3})$ 時間

【命題 4】の類似ですね。【命題 1】で出てきた式変形などを使って、小さな $b(i)$, $B(i)$ から順に計算していくことになります。例えば、Dirichlet 積の定義式から $$c(n) = a(1)b(n) + \text{より小さな $b(i)$ の寄与}$$ と書けることから、$b(1), b(2), \ldots, b(K)$ が計算できます。累積和をとれば $B(1), \ldots, B(K)$ が計算できます。$$C(n) = a(1)B(n) + \text{より小さな $B(i)$ の寄与}$$ と書けることから、$B(\lfloor N/i\rfloor)$ も小さい方から（$i$ が大きい方から）順に計算できます。

詳しい実装は紹介しませんが、後述の関連問題を解きながら細部を考えてみてください。

【命題2】の類似は成り立ちません。つまり、$1$ 点での値 $C(N)$ だけが欲しい場合にも、大きな $N$ での $C(N)$ の計算に小さな $C(i)$ の値が必要となるため、$O(N^{2/3 + \epsilon})$ の形の計算量になります。

具体例

代表的な Dirichlet 級数として、$\zeta(s) = \sum_{n=1}^{\infty}n^{-s}$ があります。また、この平行移動 $\zeta(s-k) = \sum_{n=1}^{\infty}n^kn^{-s}$ も頻出でしょうか。これらの組合せだけでも、有名な数論関数がかなり網羅できてきます。

約数関数の累積和

$\sigma_k(n) = \sum_{d|n} d^k$ としましょう。特に、$k=0$ ならば約数の数え上げ、$k = 1$ ならば約数の和です。Dirichlet 級数は

$\sum_{n=1}^{\infty} \sigma_k(n)n^{-s} = \zeta(s)\zeta(s-k)$ と表すことができます。

$\zeta(s)$ や $\zeta(s-k)$ については、$n$ 番目の取得や、$n$ 番目までの累積和の取得は、$k$ を定数と見た場合 $O(1)$ 時間で計算できます。したがって、その $N$ 番目までの総和は、【命題 1】より $O(\sqrt{N})$ 時間で計算できます。

この例は、結局のところ $\sum_{ij\leq N}i^k$ の計算を、少なくとも一方は $\sqrt{N}$ 以下であることに注目して計算しているだけで、きわめて基本的です。これまでの命題について、簡単な場合にロジックを見直したいときに役に立つのではないでしょうか。

$\lfloor N/i\rfloor$ 番目までの総和をすべての $i$ に対して列挙したい場合には、【命題 4】より $O(N^{2/3})$ 時間で計算できます。

Möbius 関数の累積和（Mertens 関数）

Möbius 関数 $\mu(n)$ の累積和 $M(n) = \sum_{i=1}^n\mu(i)$ は、Mertens 関数 と呼ばれます。Möbius 関数は Dirichlet 積においてはとても基本的で、$\zeta(s)$ の逆元に相当します：$$\frac{1}{\zeta(s)} = \sum_{n=1}^{\infty}\mu(n)n^{-s}.$$

【命題 5】を用いることで、Mertens 関数 $M(N)$ は $O(N^{2/3})$ 時間で計算できることが分かります。

Euler 関数の累積和

Euler 関数 $\varphi(n)$ について、次が基本的です：$n = \sum_{d|n}\varphi(d)$。つまり、$\zeta(s-1) = D_{\varphi}(s)\zeta(s)$ が成り立ちます。$D_{\varphi}(s) = \frac{\zeta(s-1)}{\zeta(s)}$ であることが分かります。

なお、このことは、$\varphi(n)$ の素因数分解による計算法を表した Euler 積 $$D_{\varphi}(s) = \prod_{p} (1 + (p-1)p^{-s} + (p^2-p)p^{-2s} + \cdots) = \prod_{p}\frac{1-p^{-s}}{1-p\cdot p^{-s}}$$ からも確かめられます。

$\zeta(s)$ と $\zeta(s-1)$ に対して【命題 5】を用いることで、$\sum_{i=1}^N \varphi(i)$ は $O(N^{2/3})$ 時間で計算できることが分かります。あるいは、$D_{\varphi}(s) = \zeta(s-1)\cdot \frac{1}{\zeta(s)}$ から、Mertens 関数と【命題 4】を用いてもよいでしょう。

無平方数 (square-free number) の数え上げ

$p^2|n$ となる素数 $p$ が存在しないときに、$n$ は無平方 (square-free) であるといいます。$N$ 以下の無平方数を数え上げたいとしましょう。これは、Dirichlet 級数

$$f(s) = \prod_p (1 + p^{-s})$$

における $n^{-s}$ の係数の累積和を求めよという問題です。$1 + p^{-s} = \frac{1-p^{-2s}}{1-p^{-s}}$ より $f(s) = \frac{\zeta(s)}{\zeta(2s)}$ です。よって、$f(s)\zeta(2s) = \zeta(s)$ なので、$\zeta(s)$ や $\zeta(2s)$ を【命題 5】の形で管理できればよさそうです。

$\zeta(2s)$ は、平方数に対してのみ係数 $1$ を持つという単純な形をしているため、累積和も平方数の数え上げとして容易に行うことができます。よって、$N$ 以下の無平方数の数え上げは $O(N^{2/3})$ 時間で行うことができます。

疎な変形

少し難しい例も扱っておきましょう。例えば、$a(n) = \sigma_0(100n)$ （$\sigma_0$ は約数の個数の数え上げ関数）として、$\sum_{n=1}^N a(n)$ を求める問題を考えましょう。

$\sigma_0(n)$ や $a(n)$ は $n$ の素因数分解を元に計算できます。これは、Dirichlet 級数 $D_{\sigma_0}$, $D_a$ が 「Euler 積分解」を持つことを示しています。例えば、

  • $f_p(s) = 1 + 2p^{-s} + 3p^{-2s} + \cdots = \frac{1}{(1-X)^2}$ （ただし $X = p^{-s}$）とおく
  • $D_{\sigma_0}(s) = \prod_{p} f_p(s)$ が成り立つ

ことが分かります。$n$ が $p$ で $k$ 回割り切れるときに、$k + 1$ をかけていく。という計算手順が、項 $(k+1)p^{-ks}$ に対応しています。なお、$D_{\sigma_0}(s) = \zeta(s)^2$ でしたが、その表示と $\zeta(s) = \prod_p (1-p^{-s})^{-1}$ を利用しても同じ結論に至ります。

$D_a$ はどうでしょうか？$n$ が $p$ で $k$ 回割り切れるときの計算ですが、$p\neq 2, 5$ については $\sigma_0$ と変わりません。したがって、$D_a$ は $D_{\varphi}$ から疎な変形を行う形で表すことができます。

  • $g_2(s) = 3 + 4X + 5X^2 + 6X^3 + \cdots$ （ただし $X = 2^{-s}$）
  • $g_5(s) = 3 + 4X + 5X^2 + 6X^3 + \cdots$ （ただし $X = 5^{-s}$）

とすると、$D_a(n) = \prod_{p\neq 2, 5}f_p(s)\cdot g_2(s)\cdot g_5(s)$ と書けることが分かります。

$$D_{a}(s) = D_{\sigma_0}(s)\cdot \frac{g_2(s)g_5(s)}{f_2(s)f_5(s)}$$ となります。$F(s) = \frac{g_2(s)g_5(s)}{f_2(s)f_5(s)}$ はとても疎な Dirichlet 級数で、$n = 2^a5^b$ のところにしか $0$ でない値を持ちません。

したがって、そのすべての項の計算や、累積和の計算は容易に行うことができ、 $\sum_{n=1}^N \sigma_0(100n)$ は $O(N^{2/3})$ 時間で計算できることが分かります。また、$F$ が非常に疎であることを利用すると $\sigma_0$ の累積和は $n = \lfloor N/(2^a5^b) \rfloor$ の形の $n$ についてしか行う必要がないことも分かり、全体として $O(\sqrt{N})$ 時間で計算することもできます。

「疎な変形」としては、このように少数の素数部分の変形や、あるいはどの $p$ でも $2$ 乗以上で割り切れる数（powerful number）部分の変形が代表的だと思います。

関連問題

Project Euler は、コンテンツの性質上さらなるヒントや解答コードの提示はできませんので、ご了承ください。

問題例：Multiple Sequences (ARC 116 [C])

本記事を執筆する直接的なきっかけとなった問題です。

C - Multiple Sequences
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp

記号を適宜取り換えて、$A_i$ を比に取り換えることで、次の問題であることが分かります。

自然数の組 $(A_1, \ldots, A_M)$ であって、総積が $n$ であるものの個数を $f_M(n)$ と書く。$\sum_{n=1}^N f_M(n)$ を求めよ。

解法 1：$O(N^{2/3}\log M)$ 時間解法

$$\zeta(s)^M = \sum_{n=1}^{\infty} f_{M}(n)n^{-s}$$ が成り立ちます。つまり、興味のある数列は、$\zeta$ を Dirichlet 積に関して $M$ 乗したものです。

Dirichlet 級数について、必要な情報を【命題 4】の形で管理することにします。$\zeta^i$ は常に乗法的なので、Dirichlet 積の計算は $1$ 回あたり $O(N^{2/3})$ 時間で行えます。

これを $M$ 回計算するとひどい計算量になってしまいますが、Dirichlet 積は結合的なので繰り返し二乗法を適用でき、全体として $O(N^{2/3}\log M)$ 時間で計算できます。

AtCoder コードテスト環境で、$N = M = 10^9$ を 3 秒で計算することができています。

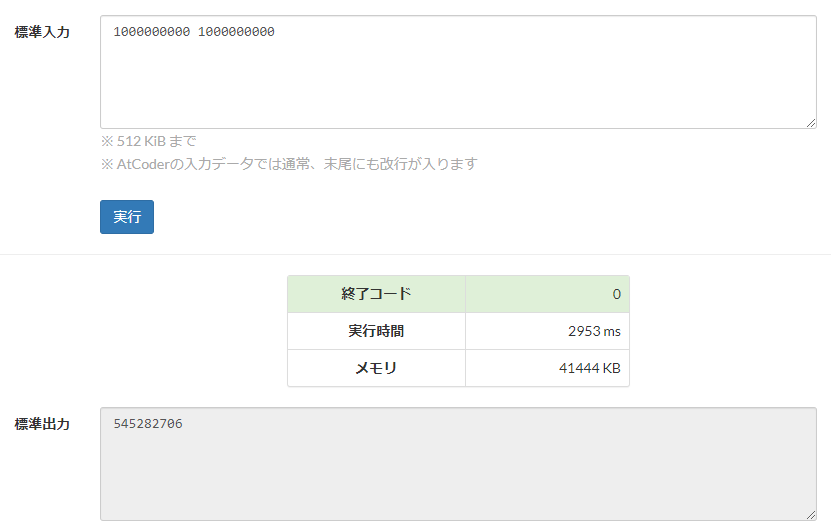
解法 2：$O(N^{2/3}\log N)$ 時間解法

$2$ 以上の 自然数の組 $(A_1, \ldots, A_m)$ であって、総積が $n$ であるものの個数を$g_{m}(n)$ と書くことにします。$G_m = \sum_{n=1}^Ng_{m}(n)$ とすれば答は $\sum_{m}G_m\binom{M}{m}$ です。$2^m > N\implies G_m = 0$ であることはすぐに分かるので、$0\leq m\leq \log_2n$ に対して $G_m$ を計算すればよいです。

ここで、$\sum_{n=1}^{\infty}g_{m}(n)n^{-s} = (\zeta(s)-1)^m$ が成り立つことが分かります。「$2$ 以上の自然数」というルールなので、$\sum_{n\geq 2}n^{-s} = \zeta(s)-1$ を用いています。

二項定理で展開することで、$\zeta(s)^i$ $(0\leq i\leq \log_2 n)$ に対する $N$ 項累積和が計算できればよいと分かります。やはり、$\zeta$ を $1$ 回ずつ畳み込んでいけばよいです。

解答例：https://atcoder.jp/contests/arc116/submissions/21380945 （$O(N^{2/3}(\log\log N)^{1/3})$ 時間計算量での実装）

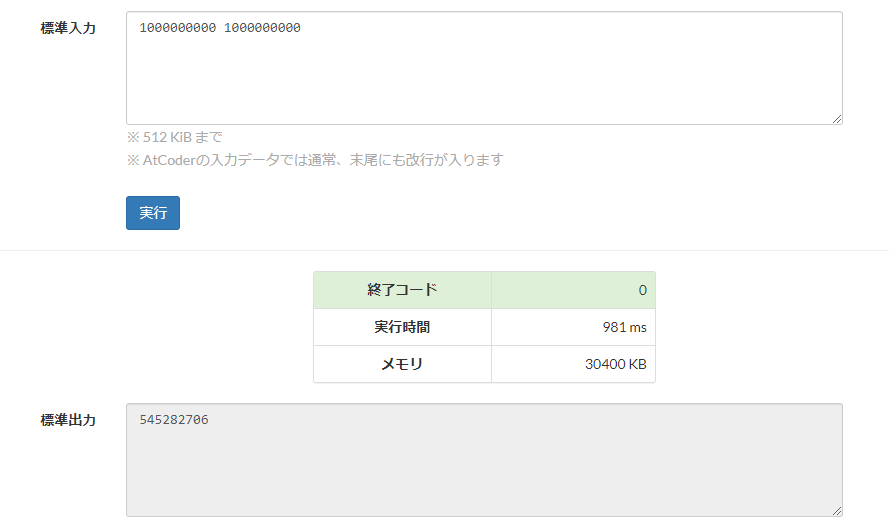
$N = M = 10^9$ に対して、約 1 秒の実行時間を実現できました。上の解法と比べて高速になりましたが、

  • 繰り返し二乗法の乗算回数 $O(\log N)$ 回よりも、この解法の乗算回数 $O(\log M)$ 回の方が、定数倍が小さい
  • こちらの解法は、乗算の対象が常に $\zeta(s)$ であるため、それを陽に配列として持つ必要がない

といった性質が挙げられます。

参考文献

スポンサーリンク
タイトルとURLをコピーしました