A. Plus and Square Root
$k(k+1)$ の形を保つように操作していくことができます.
B. Complete The Graph
未定の辺重みを $(0,0,\ldots)$ から $(\infty,\infty,\ldots)$ まで適当な順にインクリメントしていくことを考えると,最短路長はインクリメントによって高々 $1$ しか増えません.よって適当なインクリメント順の列を作って二分探索すればよいです.
C. Digit Tree
重心分解することで,根を通るパスについて調べることに帰着されます.
根までの digit 列を $a$,根からの digit 列を $b$ とすれば $10^{|b|}a+b\equiv 0\pmod{M}$ という条件になりますが,$M$ は $10$ と互いに素なのでこれは $a\equiv 10^{-|b|}b$ と変数分離できるので数えられます.
D. Create a Maze
おおよそ $(2,2)$ 進むごとに $6$ 倍にしていくような構築で解きました.
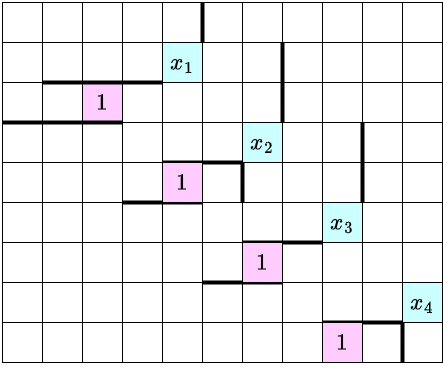
上図では $T=1234$ の出力で,$x_2=6x_1+4$, $x_3=6x_2+1$, $x_4=6x_3+4$ が成り立っています.ちょうど $1$ 通りになるようなマスと並走しながら適当な方法で合流させることで,$6x+0, \ldots, 6x+5$ のすべてを作ることができます.
E. Complete the Permutations
$O(N^2)$ で解けるはず(私の提出はさぼり $3$ 乗).
まず「distance」は有名問題で,$p_i\to q_i$ に辺を張ったときのサイクルの個数と対応します(サイクルの個数が $N – \text{distance}$).よってサイクルを数えましょう.
$v\to v$ という辺があるときそれは消してサイクルの個数を $1$ 足しておきます.入力で $x\to v$, $v\to y$ となる $v$ がある($v$ は頂点で,$x,y$ は頂点または未定)とき,これを $x\to y$ に置き換えてよいです.
この処理をすべてやったあとでは入力の $p,q$ の両方に現れる頂点は存在しないとしてよいです.さらにこの時点で辺 $v\to w$ があれば,$v, w$ を縮約してもサイクルの個数は変わらないため,この辺を入力から消してしまってもよいです.
結局
- $p,q$ の両方に現れている頂点は存在しない
- 各 $i$ について $p_i,q_i$ どちらかは未定.
としてよいです.$p$ にだけ現れている点をタイプ $0$,$q$ にだけ現れている点をタイプ $1$,そのほかをタイプ $2$ としておおよそ次の問題に帰着されます.
- タイプ $0$, $1$, $2$ の頂点がある(ラベル付き).これらの順列であって,「タイプ $0$ の頂点の行き先はタイプ $1$ ではない」という条件を満たすものを,サイクルの個数ごとに数えよ.
包除原理を使います.行き先がタイプ $1$ であるようなタイプ $0$ の頂点数を固定するごとに数えればよいです.これも包除ルールの辺は縮約してしまって考えればよいので,単に順列をサイクルの個数ごとに数えるという有名問題(第 $1$ 種スターリング数)に帰着されます.

