A. Cake Assignment
逆順に操作していけばよいです.一意に決まっていって,$2$ で割れる回数が増えていくことから初期状態に到達します.
B. Antiamuny Wants to Learn Swap
321 avoding sequence(あるいは LDS 2 以下)ということになります.なぜならばそのような $3$ 要素のうち右端と左端の距離が最小であるものをとると,転倒を解消するスワップの繰り返しでその $3$ 要素を隣接させられて,$2$ 種類目の操作を転倒を $3$ 減らす形で使えてしまうからです.逆にそのような $3$ 要素がなければ転倒を $3$ 減らす操作ができるタイミングは発生しません(操作 2 は高々 1 回までなので).
$R$ をインクリメントしながら,同じ $R$ に対するクエリにまとめて答えます.このためには,$A_1,\ldots,A_R$ に対する長さ $3$ の減少列であって左端が最も大きいものを適当な方法で求めておけばよいです.
C2. Maple and Tree Beauty (Hard Version)
longest common subsequence といっていますが,longest common prefix としてよいです.prefix を使わないパターンがあるとして適当なスワップ操作で使う場所の深さを小さくするという議論で示せます.
葉の深さを $d$ とします.長さ $k$ が達成できるかどうかですが,$k\leq d+1$ が必要です.あとは深さ $k$ までのところで同じ深さのところに同じ値を書いて,目標の個数分布にできるかどうかです.bitset を持って subset sum の dp しながら,ある区間に true があるかを見ていけばよいです.
D. Antiamuny and Slider Movement
すべての $i$ について独立に解きます.制約が小さい.
$i$ を固定すると,
- $x=a_i$ で初期化.
- 「$x:=v$」「$x:=\min(x,v)」「$x:=\max(x,v)」という $3$ 種のクエリを並べる.
ということになります.
さらに適切な座圧を行って,次のことを $O(Q)$ 回計算することにします:「最終的な位置が $x$ 以上になるような操作列は何通りありますか?」
$x$ を固定してこの問題を考えると,$x$ 以上の座標を $1$,その他を $0$ として扱えばよくなります.$\mathrm{chmin}(x,1)$ と $\mathrm{chmax}(x,0)$ は無視,その他のクエリはすべて代入操作として扱えます.代入操作のうち最後に来るものはどれかだけに興味があるので,順列が条件を満たす確率が簡単に計算できます.
適切にやると $O(NQ)$ 時間程度になると思いますが,毎回雑な座圧で $O(NQ\log Q)$ 時間使っても大丈夫です.
E2. Determinant Construction (Hard Version)
私は E1 を経由せず直接 E2 という感じでした.
tridiagonal に作ることを考えます.
det は dp で計算できます.各行から $1$ つずつ選ぶ方法について考えて,「$i$ 行目までを選んだ時点で $[0,i+1]$ 列目のうち $i,i+1$ のどちらかだけまだ選んでいない」という $2$ 状態を持つようにします.
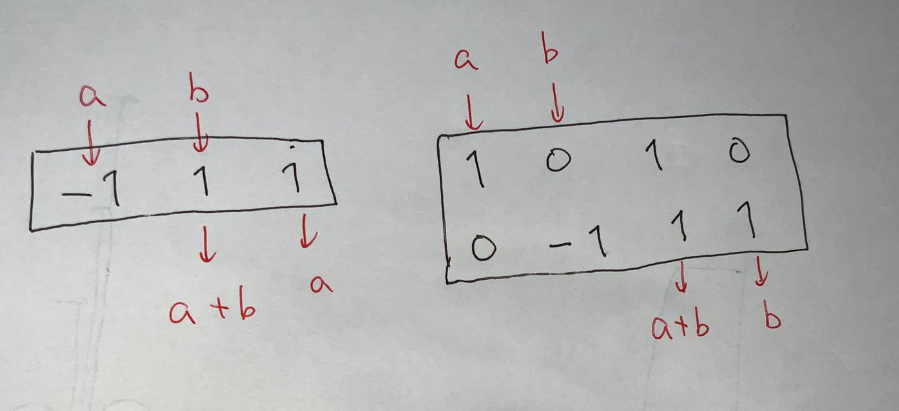
私はこの 2 種を実装したのですが,考えるまでもなく後者はスワップと前者でしたね(終了後に気づいた).
$(\pm 1,\pm 1)$ からスタートしてこれらの操作で和が $N$ の状態に持っていけばよいです(コンテスト中はこれも $(N,x)$ を作ろうとしていてコスト $1$ を損していた).
$(N,x)$ を互除法のように戻していって $(\pm 1,\pm 1)$ にするときのコストが目的の値以下になれば成功です.このような $x$ は乱択で簡単に見つかるようです.
F. Ode to the Bridge Builder
コンテスト中はスルーしましたが,難しくはないと思います.
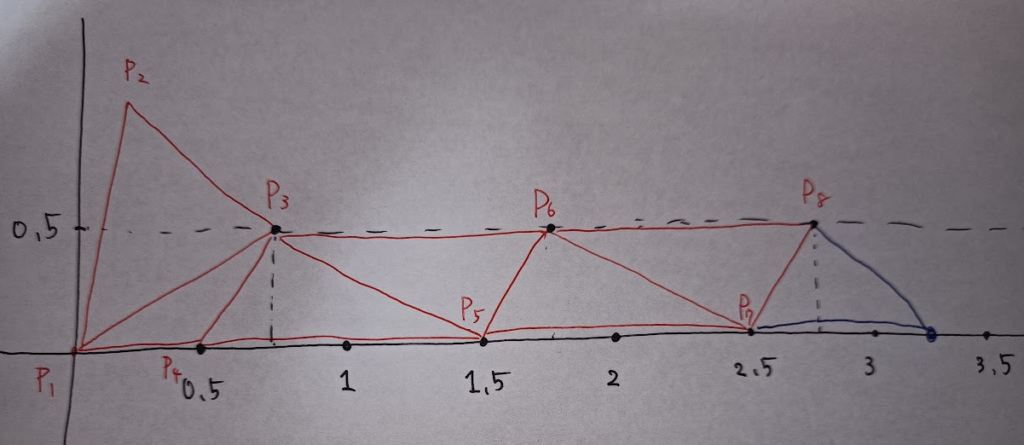
座標変換して,次のようにして考えました:$P_2$ は第一象限内で $P_1P_2=1$ である.目標地点は $(d,0)$ で $m=\lceil 2d\rceil$ である.だいたい $2$ 回の操作で距離 $1$ ずつ縮めていくということを考えます.
$M$ が偶数の場合,だいたい次のようにすればよいです.
- $P_3(0.5, 0.5\sqrt{3})$ とする.
- $P_4(1,0)$ とする.
- $P_{k+2}$ を $P_k$ を $(1,0)$ 平行移動したところに作る.
$P_1P_3=0.5$ にとっている時点で,$0.5\leq P_2P_3$ は大丈夫です.$P_2P_3\leq 1$ も確かめられます.あとは状況が全部平行移動されていくだけなのであまり問題は起きません.
最後の $1$ ステップについては,$P_3$ から見て $x$ 軸上の区間 $[0.5,1]$ が距離 $0.5$ 以上 $1$ 以下になっていることの平行移動なので大丈夫です.
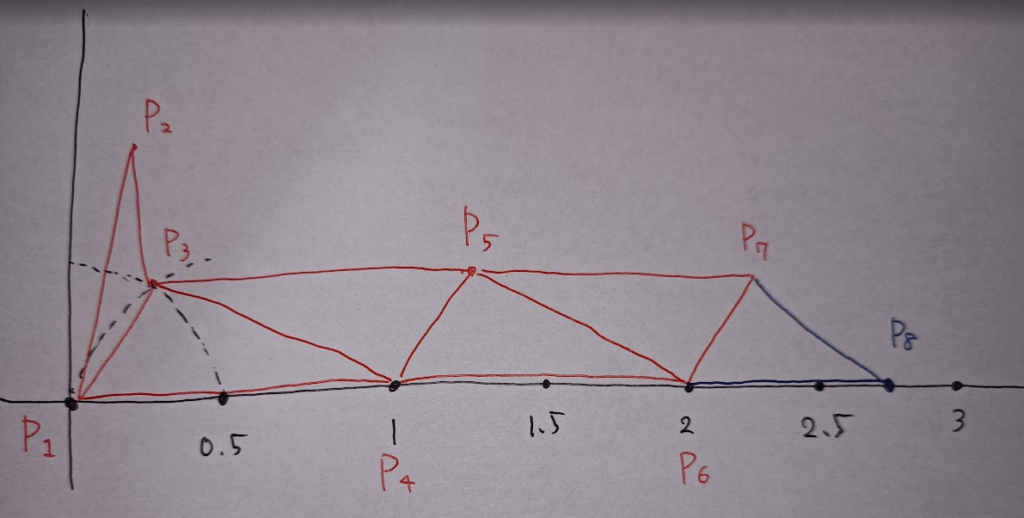
$M$ が奇数の場合もだいたい同じようにします.$P_3,P_4$ が $(0.5,0), (0.75,0.5)$ またはそのスワップになるようにします.$P_2$ の初期位置によって適切な方を選べばうまくいきます.
あとはこれらを平行移動した点 $(0.5+k,0), (0.75+k,0.5)$ を順に作っていけばよいです.