A. Sieve of Erato67henes
$67$ は素数なので,$67$ の倍数があるという条件になります.
というわけで $67$ の倍数を作る問題だと思って解いてしまいましたが,制約から同値だったみたいですw
B. Heapify 1
自由にスワップ可能な $2$ 点を同じ成分としたときに,各成分内で好きにソートできます.
C. Dice Roll Sequence
向かい合う面同士を同じ状態と考えて $3$ 状態としてしまってもよいです.
最後の面を状態として dp を考えればよいです.貪欲でもいいね.
D. Absolute Cinema
$f(i+1)-f(i)$ を求めることで,$(a_1+\cdots+a_i)-(a_{i+1}+\cdots+a_n)$ のような和が求まります.
さらにその隣接差分から,$a_2,\ldots,a_{n-1}$ が求まります.
この状態から $a_1,a_n$ は,$f(n),f(1)$ から求まります.
E. Idiot First Search
$v$ から親に移動するときには印が消えているのが重要です.これをもとに,
- $dp[v]$:$v$ に居て印が何もないときに,親に移動するまでの移動回数.
として dp ができます.あとはこの値を根までのパスについて足したものが答となります.
F. Parabola Independence
独立集合を選ぶことは,$i_1,i_2,i_3,\ldots$ を選び,任意の $x$ で $f_{i_1}(x)<f_{i_2}(x)<\cdots$ が成り立つようにすることです.
結局 DAG があって,頂点ごとにそれを通る最長パスを求めるという問題になります.どのような DAG かというのは「任意の $x$ で $f_i(x)<f_j(x)$ ですか」を全点対で判定すればよいです.$2$ 次関数の判別式などを用いればよいです.ただし $x^2$ の係数が一致するもの同士の比較に注意します.
G. Idiot First Search and Queries
混乱したので強めの道具を使って対処しました.
$dp[v]$:$v$ に居て印が何もないときに,親に移動するまでの移動回数.これは求めておきます.modint ではなく適当な INF で chmin しておけばよいです.
第 $1$ フェーズとして,これを使ってまずなるべく親方向に移動させます.
binary lifting や HLD などの適当な木上のパスに関する二分探索でよいですし,私は後述の実装と合わせて平衡二分木を持ち出して処理しました.
第 $2$ フェーズとして,子方向に移動させていくことで答を確定させます.各頂点で,組 (steps, query index) のソート列を保持するというイメージです.親から受け取ったソート列に,第 $1$ フェーズで $v$ に置かれているクエリのデータを挿入します.
このうち steps が $0$ であるような prefix の答が $0$ です.steps が $1+dp[left(v)]$ 未満であるようなクエリは左部分木で処理されるため,$1+dp[left(v)]$ を全体から引いて左にもぐるということにします.ソート列の左の方を split して,全体加算という感じの処理ができればよいことになります.このような処理を平衡二分木で実装すればよいです.
第 $1$ フェーズで $\log^2$ 計算量にしてしまいましたが,これの回避は容易です.最小値取り出しだけなので meldable heap の類や単に prique などを使っても良かったかもしれません.
H. Codeforces Heuristic Contest 001
流石に自由度が高そうなので,ある程度大きければ全点回収できるだろうと予想しました.
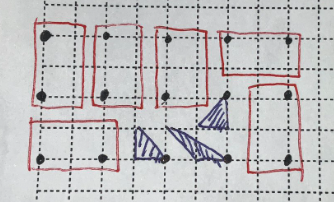
$2\times 3$ の長方形がとれることに注目します.すると,$2n\times m$ の構築を $2n\times (m+3x)$ にしたり,$n\times 3m$ を $(n+2x)\times 3m$ にしたりできます.特に $9\times 9$ ができれば万事解決ということになります.
はじめ,$3\times 5$ や $3\times 7$ などで(プログラミングすらせず手作業で)適当にすぐ見つかるだろうと予想していたのですが,これは失敗でした.これは例えば $3\times 5$ には $(2i,2j)$ に相当する点が $6$ 個あり,$5$ 個の三角形のうちどれか $1$ 個はこの種類の点を $2$ 個使ってしまうからです.
そこで $5\times 9$ を考えました.この場合,$(2i,2j)$ に相当する点が $15$ 個あって三角形も $15$ 個なので,このタイプの点を $1$ つずつ使っていくように注意します.このことに注意しながら $2\times 3$ の長方形を適当に処理していけば,見つかりました.