A. Needle in a Haystack
置ける文字のうち最小の文字を置くということを繰り返します.「置ける」とはどの文字種類についても $t$ での個数は $s$ での個数以上であるということです.ただし,置く文字が $s$ の先頭文字ならばそれも置いた文字とともに削除して判定ということになります.
結局初期状態で矛盾がないなら,
- $s$ の先頭文字は置ける($s$ の先頭の文字とともに削除)
- そうでないものは,$s$ での頻度よりも $t$ での頻度の方が多いときに置ける
というようになります.
B. Wishing Cards
$O(n+k^3)$ が(定数倍がひどくなければ)間に合うことに注意します.評価は $\sum k^3 \leq \sum k\cdot k_{\max}\cdot k_{\max} \leq 1800\times 360 \times 360$ の要領です.
$b$ について,$b$ の非零項は単調増加としてよいです.さらに,$x$ について $b_i=x$ となる $i$ が存在するならば,そのような $i$ は $x\leq a_i$ となる中で最小のものとしてよいです.
特に,非零項 $b_i$ を置くべき場所とその値の組は $O(k)$ 通りしかありません.その時点までで置いた最大の $b_i$ および,$b_i$ の総和を状態とする dp によって,$O(k^3)$ 時間.事前に置く場所の候補を列挙する処理も合わせて $O(n+k^3)$ 時間でできます.
C2. Beautiful Patterns (Hard Version)
$I, J$ などを区間として,$x_I$ を回文かどうかによって $0,1$ と定めるとき,求めるべきは $(\sum_I x_I)^2 = \sum_{I,J}x_Ix_J$ です.
そこで $x_Ix_J$ の期待値(要するに,$I,J$ が両方回文になる確率)を考えます.結論として,
- $I, J$ の回文の中心が一致するとき:大きい方の区間が回文になる確率.つまり $k=\max(|I|,|J|)$ として $(1/m)^{\lfloor k/2\rfloor}$.
- それ以外:$k_1=\lfloor |I|/2\rfloor$, $k_2=\lfloor |J|/2\rfloor$ として $(1/m)^{k_1+k_2}$
が確率です.非自明なのは後者です.$I$ が回文という条件が来ると,$\lfloor |I|/2\rfloor$ 個の組について,こことここは等しいという条件が来ます.これをグラフの辺で表します.連結成分上で一定という条件があることになります.$2$ つの区間 $I,J$ についてこのような辺を張ったとき,グラフが森になる(実際にはより強くパスに分解)されるということが分かります.
証明します.$I$ にのみ含まれる要素があるとき,グラフに次数 $1$ の頂点があって,この頂点と辺を削除した上で示せばよいです.これは,$I$ から両端の文字を消して示せばよいということを意味します.中心が不一致だと $2$ つの区間は異なるので,どちらかの区間にこの処理をすることができて,処理結果でも中心が不一致になるので,これを両区間が長さ $1$ 以下になるまで行えて証明が完了します(あるいは長さについての帰納法).
以上を踏まえて問題を解きます.まず $x_Ix_J$ を $(1/m)^{k_1+k_2}$ だと思って答を計算します.区間の価値を $(1/m)^{k_1}$ に置き換えて,価値の総和を $2$ 乗すればよいです(コンテスト中の私は convolution を召喚して $k_1+k_2$ の分布を求めています).
あとは中心の位置を固定するごとに解きます.$O(N^3)$ 時間にはすぐになると思いますが,$\sum r^i$ や $\sum i\cdot r^i$ などの計算を利用することで $O(N\log N)$ 時間になります.これらの累積和を事前計算しておくことで $O(N)$ 時間にもなると思います.
D. Secret Message
すごい.
辺重みでソートして,先頭 $N-1$ 個が木 $T$ のときだけが問題です.
ここからひとつ外してひとつ追加するパターンを計算しておきます.
$2$ つ以上外して $2$ つ以上追加するパターンについて考えます.
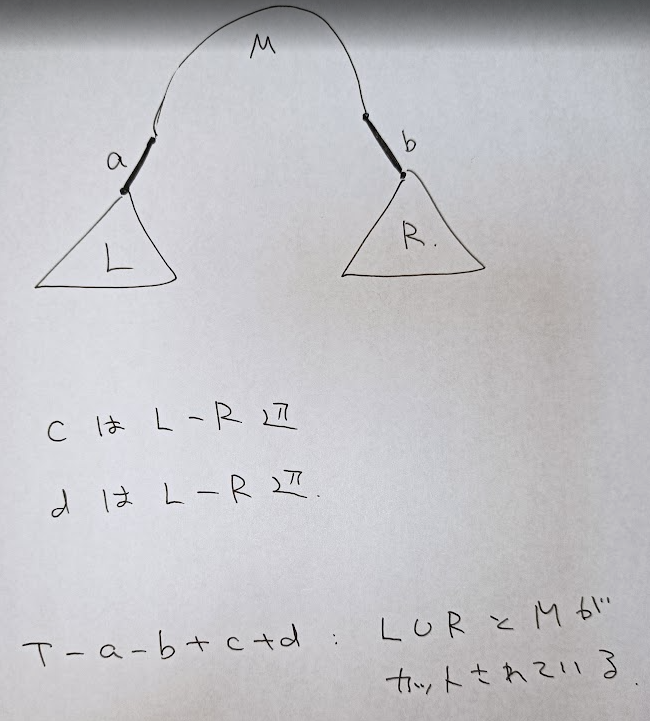
$n-2,n-1,n,n+1$ 番目の辺重みを $a,b,c,d$ とします.サイクルを作るという条件を無視すれば,$2$ つ入れ替えるパターンで重みが最小なものは $n-1$ 個の和から比べて $-a-b+c+d$ する選び方です.
– $a, b$ が $T+c$ のサイクルに含まれていない場合:$T+c-a$ や $T+c-b$ のコストがこれを下回る.
– $a, b$ が $T+d$ のサイクルに含まれていない場合:$T+d-a$ や $T+d-b$ のコストがこれを下回る.
これらの場合を除くと,必ず $T+c+d-a-b$ はサイクルを含みます.
E1. Game of Scientists (Version 1)
$b$ 進 digit sum から,$\pmod{b-1}$ での値が取り出せることを利用します.
- $b = 44730$ として,$\mod b-1, b-2, b-3, b-5$ での値を決めると ANS が決まる.ただし $ANS < b-5$ だと失敗.
- このまま $3$ 乗根をとると少し足りない.$33$ を聞き,$-1$ 以外だったら次に $66$ を聞く.ここで $-1$ だった場合も確定することに注意.あとは $66$ 以下の適当なものを聞いて,$44730$ 以下をカバーする.
- $32$ 以下だと確定していて残り $2$ 回の状況だとする.$4$ を聞き,返答に応じて次は $2$ または $8$ を聞くと決定できることが分かる(全探索など)
これでできています.
E2. Game of Scientists (Version 2)
単調減少に聞く方針だと評価が足りないので初手に割と小さい数を聞く勇気を持ちます.
$[1,x]$ が $1$ 回で特定できる $x$ は $x=3$ までです.
それを踏まえて $[1,x]$ が $(4, b)$ の $2$ 回で特定できるようにしようとすると,$b=8$ で $[1,32]$ までだと分かります.
つまり,$2$ 回あれば $[1,32]$ に対応できます.これを踏まえて初手を $b=33$ として,$-1$ が返ってきた場合は上のようにします.
やはり,$[33,x]$ を処理できるような強いものを全探索で探すと,$(33,66)$ の $2$ 回で $[33,2178]$ が処理できることが分かります.これを踏まえて $2$ 回目は $2178$ を質問します.
ここまでまとめ.
- $query(33)$ で $-1$:$2$ 回で $[1,32]$ を解く.
- $query(33)$ のあと $query(2178)$ で $-1$:$query(66)$ を利用して解ける.
- 残りの課題:$query(33), query(2178)$, あと $1$ 回で決定したい.答えは $2178$ 以上が保証.
$query(33), query(2178)$ だけでどこまで確定できるかを探索すると,$70000$ 程度まではこの $2$ つの情報で行けます.なので,$3$ 回目は $70000$ 程度まで使えます($-1$ が返ってきても復元可能).
$32, 2177, p$ が互いに素な $p<70000$ を適当にとって $query(p+1)$ をして,$-1$ が返ってきたら上の通り復元.そうでなければ $\mod 32\times 2177\times p$ で一意で,これは $2\times 10^9$ に十分到達しています.
F. Mosaic Tree
次数列を決めたときの木の個数の数え上げを思い出します.おおよそ次のようになります(次数 $d_i$ の代わりに $d_i-1$ を考えています).
- $\sum d_i=n-2$ となる列 $(d_i)$ について,$\sum \frac{1}{d_1!\cdots d_n!}$ を総和せよ.
- ただし,各 $j$ について,「色 $j$ の $i$ に対する $d_i$ の総和の parity はこれ.」という条件がつく.
parity の条件がなければ,単に $f(x)=\sum_{d}\frac{1}{d!}x^d$ として $[x^{n-2}]f(x)^n$ を求めればよいということになります.$f(x)=e^x$ で,行列木定理が導出されます.
ここに色ごとの parity の条件を入れます.色 $j$ について $k$ 個の頂点があるとして,「$e^{kx}$ の偶数次だけ残した FPS」「$e^{kx}$ の奇数次だけ残した FPS」などをとり,これを色に対する母関数とします.これを色について総積をとればよいです.
結局,$\frac{e^{kx}+e^{-kx}}{2}$ や $\frac{e^{kx}-e^{-kx}}{2}$ をたくさんかけてくださいということになります.ただし $\sum k= n$ です.
$(t^k\pm t^{-k})$ をかけたあとで $t=e^x$ を代入すると思います.次数の和が $O(n)$ であるような多項式総積に帰着されて,$O(N\log ^ 2 N)$ 時間です.
愚直にかけていっても $O(n^2)$ 時間で,mod や $n$ の制約を見る限り,こっちを意識して作問されているかもしれません.

