A. Greedy Grid
$2\times 3$ を含むと反例が構築できます.含まないときに反例がないことも簡単に分かります.
B. Pile Shuffling
自由位置への挿入を反復する場合のよくある言い換えとして,「まず削除操作を行う」「最後にまとめて挿入操作を行う」というものがあります.
全体での $0,1$ の個数が初期状態と目標状態で等しいので,削除操作で目標状態の subsequence にできれば目標達成です.何回削除すると subsequence になるかを各山について計算します.
C. Manhattan Pairs
実は $x, y$ 独立に最適化した場合の最大値が実現可能です.
$x, y$ それぞれ上位半分,下位半分ずつに分けます.
- $A$:$x$ が上位で $y$ が上位であるような点全体
- $B$:$x$ が上位で $y$ が下位であるような点全体
- $C$:$x$ が下位で $y$ が上位であるような点全体
- $D$:$x$ が下位で $y$ が下位であるような点全体
とすると,$|A|=|D|$, $|B|=|C|$ が成り立ちます.実際 $|A|+|B|$, $|B|+|D|$, $|A|+|C|$ はどれも $n/2$ であることから分かります.よって $A$, $B$ 間,$C$, $D$ 間でマッチングを作るようにすればよいです.
D. Traffic Lights
最小時刻を $T$ とします.$T$ は dijkstra で計算可能です.また答は $O(NT)$ 時間で計算可能です,これは (頂点, 時刻) を状態として各状態から遷移が $O(1)$ 通りの dp で解けるからです.
面白いのは $T=O(N)$ が成り立つことです.
これは,単なる重みなし無向グラフとしての最短路に沿って進むことを考えれば示せます.最短路長を $L$ とすると
- 最短路に沿って進む回数:$L$ 回
- 最短路に含まれるその他の近傍に進もうとしてしまう回数:$L-1$ 回
- 最短路に含まれない頂点に進もうとしてしまう回数:$3(N-L)$ 回
となるからです.最後の項目については,行先の頂点を固定して考えるとよいです.
E. Greedy Grid Counting
$(i,j)$ のマスを $(i,i+j)$ に書くことで,「右または右下に進む」問題として考えます.
反例のうち極小なものについて考えると,「右 $n$ 回・右下」と「右下・右 $n$ 回」という移動の比較だけが重要だと分かります.具体的には $i$ 列目の「下から上を引いたもの」を $x_i$ とするとき,
- $x_i>0$
- $x_i+\cdots+x_j<0$
となる $i,j$ があるとダメだとわかります.
列 $x$ を左から順に作りながら,「$x_i>0$ であるときの $x_i+\cdots+x_j$ としてありうる最小値」を $x_j$ を決めた時点の状態とする dp をすれば,多項式時間で計算できます.
$x_i+\cdots+x_j$ としては,$NK$ 程度までありえて,この dp を愚直に計算すると,$O(N\cdot K\cdot K^2)$ または同じ $x_i$ に対応するグリッドの定め方をまとめて $O(N\cdot K\cdot K)$ 時間の計算量になると思います.
$2$ マスそれぞれが既知・未知のパターンそれぞれについて,適当な累積和などを使って遷移を高速化します.例えば dp の値や,それとインデックスの積を累積和を使って区間加算するというタイプの実装が可能です.
私は $NK$ 状態あると思って実装していたのですが,実際には $K$ 状態しかなくて,上で説明した区間加算などを使うと $O(NK)$ 時間で解くことができると思われます.
F. Colorful Polygon
入力は $7$ 個の二項係数の積になります.
ある辺に十分近い点をひとつ作り,その他の点を十分遠くにとることで,三角形分割で使われる三角形のひとつを強制できます.このことを利用して「積」を作ります.さらに二項係数は三角形を利用して作ることができます.
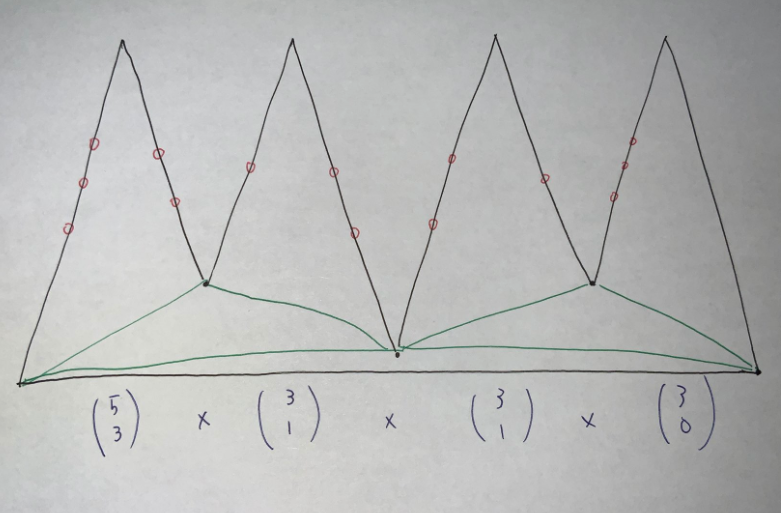
三角形の $2$ 辺に点を並べた場合に二項係数が出てくることは,例えば次のようなグリッドパスとの対応から分かります.
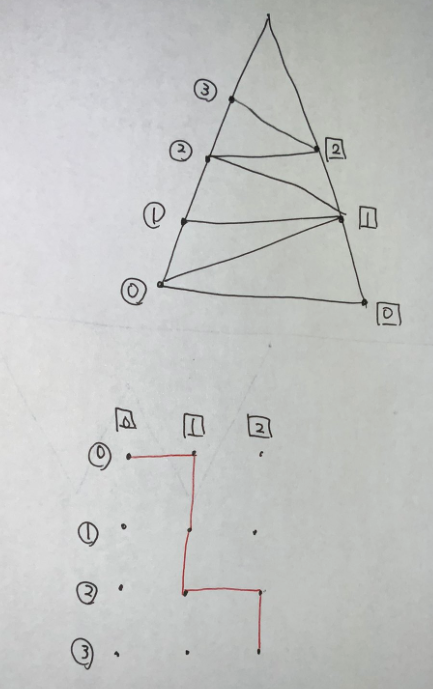
次の私の提出では,私は simple polygon といえば内角が 180 度というのは許容されないと勘違いして解いたので,三角形の $2$ 辺の代わりに放物線 $2$ つを使うという面倒な実装をしています.
辺の個数は二項係数に登場する値の総和と二項係数の個数の和の定数倍でおさえられ,二項係数を完全二分木のように作ることで制約内におさめることができます.
G. Tree Parking
AC するだけなら簡単です.実験すると有名数列が出てきて,eulerian number の計算に帰着して $O(N)$ 時間で解けます.以下,導出を考えます.公式解説とちがって母関数を用いた導出をします.
葉の個数を無視した場合
まずは葉の個数の情報を無視.根が $1$ であるという条件も無視して,$n$ 頂点の場合の根付き木の数え上げを $a_n$ とします.
頂点数 $n_1, \ldots, n_k$ の場合の subtree を持つ場合の木dpを考えれば,次が得られます.
$$a_n=\sum_{k=0}^{\infty}\frac{1}{k!}\sum_{n_1+\cdots+n_k=n-1}^{}a_{n_1}\cdots a_{n_k}\cdot\frac{n!}{n_1!\cdots n_k!}\cdot \frac{(2n-2)!}{(2n_1)!\cdots (2n_k)!}\cdot (2n-1)$$
- $1/k!$:$k$ 個の子にラベルをつけた場合の数え上げをしたあとで $k!$ で割る.
- $\frac{n!}{n_1!\cdots n_k!}$:頂点ラベル集合の分割を決める.
- $\frac{(2n-2)!}{(2n_1)!\cdots (2n_k)!}$:各 subtree での操作列をマージする方法を決める.
- $(2n-1)$:長さ $2n-2$ の操作列に,根への操作を挿入する方法.
したがって,$b_n=\dfrac{a_n}{n!(2n)!}$ とすると $2nb_n=\sum_{k=0}^{\infty}\frac{1}{k!}\sum_{n_1+\cdots+n_k=n-1}b_{n_1}\cdots b_{n_k}$ となります.$B(x)=\sum b_nx^n$ とすれば,$2B'(x)=\sum_k\frac{1}{k!}B(x)^k=\exp(B(x))$ が得られます.
葉の個数を考慮する
$a_{n,k}$ を $n$ 頂点ラベル付き根付き木であって葉が $k$ 個のものとそれに対する操作列の組の数え上げとします(本問の答の $n$ 倍).これを $x^ny^k$ の係数に持たせるという要領で $2$ 変数母関数を作ります.
$a_n=\sum_k a_{n,k}y^k$ とすれば,上の議論がほとんどそのまま葉の個数を含めても成立します.$1$ 頂点の根付き木のときだけ補正します.結論だけ述べると,$b_{n,k}=\frac{a_{n,k}}{n!(2n)!}$ とし,$B(x,y)=\sum_{n,k}b_{n,k}x^ny^k$ とするとき
$$2\frac{\partial}{\partial x}B(x,y)=\exp B(x,y)+y-1$$
という微分方程式が得られます.$c=y-1$ を定数と見て微分方程式を解くと,これは変数分離形で,結論は $B(x,y)=\log\frac{c\exp(cx/2)}{1+c-\exp(cx/2)}$ となります.
係数取り出し
$\log$ が邪魔なので微分すると,
$$[x^n]B(x,y)=\frac{1}{n}[x^{n-1}]\frac{\partial}{\partial x}B(x,y)=\frac{1}{n}[x^{n-1}]\frac{c(1+c)}{2(1+c-\exp(cx/2))}=\frac{y(y-1)}{2n}[x^{n-1}]\frac{1}{y-\exp((y-1)x/2)}$$
となります.さらに $\frac{1}{y-\exp((y-1)x/2)}=-\frac{\exp(-(y-1)x/2)}{1-y\exp(-(y-1)x/2)}=-\sum_{k=0}^{\infty}y^k\bigl(\exp(-(y-1)x/2)\bigr)^{k+1}$ を利用すれば,目的の係数が $O(N)$ 個の足し引きで計算できるようになっています($N$ 乗の類を適切に計算すれば全体で $O(N)$ 時間で答を計算できます.

