A. It’s Time To Duel
0 が隣接するというのは無理です.0 は存在します.これで必要十分になります.十分性は,01110 のようなものが作れることを確認すれば大丈夫です.
B. Slice to Survive
初手を除く着手では後手は真ん中に移動できるため,縦方向・横方向に独立に扱えます.「初手を縦方向」「初手を横方向」の $2$ 通りを計算します.
C3. Hacking Numbers (Hard Version)
知っていたので思いついたが,知らなかったら結構難しいと思う.
現在の状態の候補が $10^9$ 通りあるところからスタートしますが,add, mul, div それぞれの最悪ケースでは候補数が全然減りません.digit を上手く使う必要があります.
単に digit を連打して小さてから調整というのが C1 だと思います.
$9$ 倍してから digit を $2$ 回すると,$9$ になるので,「mul $9$ / digit / digit / add」で攻略可能です.これが C2 だと思います.
$x\leq 10^n$ の範囲で $S((10^n-1)x)=9n$ となります.$10^nL+R$ が $10^n-1$ の倍数であるとき $L+R$ も $10^n-1$ の倍数となるのでそのような $x$ に対して $L+R=10^n-1$ となることから示せます.したがって,「mul $10^9-1$ / digit」で必ず $81$ に到達可能です.
$81$ ならば $2$ 回,そうでなければ $3$ 回というのが出力すべきものです.
証明は,$2$ 回で一意になるパターンが他にないことを証明すればよいはずで,digit sum のタイミングで場合分けすれば出来ると思います.「mul / digit」というパターンに限れば $x=10^n-1$ の場合を考えるとやはり $2$ 回目で $81$ に行ってしまうというところから示せると思います.
D. D/D/D
$n\geq 2$ と連結性から適当な辺の往復を追加できるため,walk の長さを $+2$ する操作ができます.よってある長さの walk が作れるかを判定するには,その頂点までの長さが奇数・偶数の場合の最短路長をそれぞれ計算すればよいです.これは $2N$ 頂点のグラフの最短路問題を解けば計算できます.
$A_i$ の部分和をどうするかについても,総和が奇数・偶数になるパターンの中で一番総和が大きいものが何かが分かればよいです.これは dp すればよいです.
E. Binary String Wowee
ある場所の操作はそこから左にしか影響しないです.よって,右側から決めていく dp をします.
各インデックスでは,右側の flip 操作列に自分のインデックスの操作を挿入するという形で操作列を作っていきます.
前計算として,あるインデックスの初期値が 0, 1 それぞれの場合に
「右側で $a$ 回の flip が行われるときに」「自分のインデックスの flip 操作を $b$ 回挿入する」方法の数え上げを前計算しておきます.
F. Penguin Steps
$M, F$ の始点も $M, F$ と書き,ゴールを $G$ と書きます.
平面グラフ理論のこの辺を厳密にやるのが苦手なので,まあまあ雰囲気証明(あるいはそれ以下の何か)になっていますすいません.
まず,$\mathrm{dis}_M$ を計算しておきます.これは簡単にできると思います.$\mathrm{dis}_F$ は二分探索で最適化します.$\mathrm{dis}_F\geq t$ を達成できるか?という判定問題を考えましょう.達成するための最小コストが求まれば良いです.
まず $\mathrm{dis}_M$ の条件を無視します.$\mathrm{dis}_F\geq t$ というのは,$t$ 未満のマスだけでは到達不可能だということです.つまり $t$ 以上が書かれたマスを使って「$F$, $G$ の間のカット」が作れる場合です.各マスを $t$ 以上にするためのコストを求めておき,($8$ 近傍に関する)最短路問題を解くことで,カットを作るための最小コストが求まります.これが $K$ 以下であるかどうかで判定します.
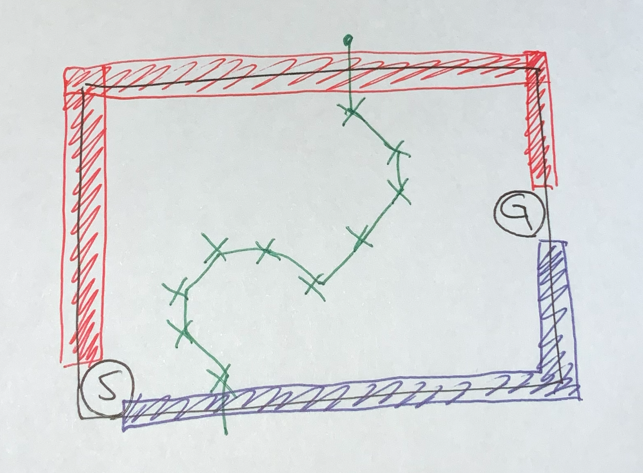
$t\leq \mathrm{dis}_M$ の場合はこれだけでよいのですが,そうでない場合には,カットを作りつつも $M$ のパスが残るようにしなければいけません.
この際,パスが残るならばそのうちで「最も左手方向に進んだパス」が残ります.このことのちゃんとした定式化や証明は私はすぐにはできないので省略します.($M, G$ が両方外側にあることで,$MG$ パスの左側・右側という概念が定義できるようになっていることとかが重要なんじゃないかな?)
そのようなパスを計算するにはなるべく左に曲がるような dfs によって,$\mathrm{dis}_M$ 以下のマスだけを通ってゴールに到達すればよいです.
最終的な解法としては,最も左手方向に進んだパス上の点での変更コストを $\infty$ に設定した上で上述の dp をやればよいです.

