概要
解説がなさそうだったので書きますシリーズ。
解法
適当に座圧しておき、座標はすべて $O(N)$ であるとします。
数え上げでは、重複・漏れなく数えるために、何らかの値によって場合分けを行うことが基本です。特に今回は、「操作手順」ではなく「操作結果」を数え上げるため、操作結果に対する場合分け軸を探しましょう
基本方針
最終的な模様は、いくつかの連結成分の直和です。
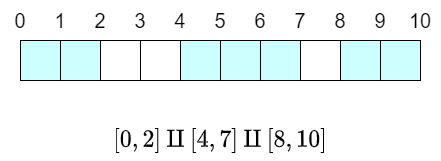
そこで、最後に現れる連結成分を場合分け軸とすると、次のような dp ができると思います。
- 座標 $i$ までを埋めて、$[i-1,i]$ が白いようなものの数え上げを、$\dp[i]$ とする。
- ぴったり $[j, i-1]$ という連結成分がありうる $j$ に対して $\dp[j]$ を足し合わせると、$\dp[i]$ が計算できる。
区間 $[L, R]$ がぴったり連結成分になるかが既知であれば、この dp は $O(N^2)$ 時間で計算できます。よって、各区間 $[L,R]$ がぴったり連結成分になることがあるかを判定することが残タスクです。
区間に対する判定問題
いくつかの $[l,r]$ の和集合がぴったり $[a,b]$ になるかという問題です。すべての $[a,b]$ に対する判定結果を、全体で $O(N^2)$ 時間で手に入れたいです。
判定を行う際には、$[a,b]$ 内の区間を全て置くとしてよいです。そこに順序を入れて、$[a,b]$ 内の区間 $[l,r]$ を $r$ 昇順で置いていくことを考えます。$[a,b]$ が完成するのは、
- $[l,r]$ を置いた瞬間
- ただし既に、$[a,l]$ は覆われている
を満たす場合です。各 $[l,r]$ を処理する時点で、「ぴったり $[a,x]$ を作ることができるような $x$ の最大値」を管理することにします。$r$ 昇順で処理するのであれば、$x$ は $r$ を超えることはなく、$[a,b]$ が完成するかどうかは $x\geq l$ であるかどうかにより判定できます。
したがって、$b$ 昇順に処理することで、ぴったり $[a,b]$ という連結成分が可能かどうかを、最後に置く区間 $[l,r]$ の候補ごとに $O(1)$ 時間で行うことができます。全ての $[a,b]$ に対する計算量の合計は $O(N^2)$ です。

