[AtCoder 参加感想] 2020/06/14:ABC 170

	A	B	C	D	E	F
問題文	■	■	■	■	■	■
自分の提出	■	■	■	■		■
結果	AC	AC	AC	AC		AC

コンテスト後提出：E → ■

全体感想
問題A – Five Variables
問題C – Forbidden List
問題D – Not Divisible
1. ゼータ変換
問題E – Smart Infants
問題F – Pond Skater

全体感想

ちょっと準備不足で参加。途中で30分+抜けることになり。
というのはあったのですが、それでも全完を落とすのはちょっとダメでしたね。

問題 E （multiset）は、Python はすこし苦手な処理で、multiset 関連については C++ の方が優れた言語選択になりそうです。PASTで頻出なんですよねこれ（笑）

問題Eで、2 * 10**5 を、2 + 10**5 とタイプミスするのをやらかしていて、20分くらい消し飛ばしました。

N = 200_000
みたいにアンダースコアを入れて宣言するのがバランス良さそうかなと思いました（3.6で追加された機能）
— おいおい瞬殺だよ (@pop_left) June 15, 2020

なるほど、是非役立てようと思います。ありがとうございました。

問題A – Five Variables

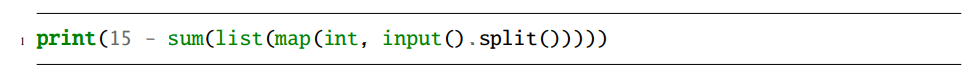
公式解説のこれですが、map object（イテレータ）をわざわざリストに変換してから和をとるのは無意味ですし、可読性やパフォーマンスの意味でも普通は利点がありません。

15 - sum(map(int, input().split()))

あるいは同じことですが、ジェネレータ式を sum 関数に入れて

15 - sum(int(x) for x in input().split())

などとするのが良いのではないかと思いました。sum 関数の引数は、iterable であれば何でもよいです（https://docs.python.org/ja/3/library/functions.html#sum）。

問題C – Forbidden List

python の min() は、順序比較のためのキーを指定できて、abs(x-X) が最小のもののうち x が最小のものをとるとかはこんな感じで書いたりできます。https://t.co/du0w3JwTkh https://t.co/BHUqFBikMx pic.twitter.com/sxwpYBK34d
— maspy (@maspy_stars) June 14, 2020

ちなみに今回の問題では、適当な範囲を全探索する解法で十分計算時間に余裕がありますが、 $O (N)$ 時間で解くこともできます。これは、 $X$ に近い整数を順に生成していけばよいです。例えば $X = 50$ ならば、「 $50, 49, 51, 48, 52, \dots$ 」順で整数を生成して、 $p_{1}, \dots, p_{N}$ に含まれないものが見つかった時点でそれを答にします。「含まれてしまったのでまだ答にできない」が起こる回数は $N$ 回以下なので、最悪でも $N + 1$ 個目の整数を生成した時点で答が見つかります。含まれるかどうかの判定に、C++ の set、python の set （C++ の unordered_set）などの適切なデータ構造を用いることで、計算量 $O (N \log N)$ あるいは期待計算量 $O (N)$ が実現できます。

提出：■

問題D – Not Divisible

整除関係を抽出する問題です。 $y$ が $x$ の倍数であるとき、 $x ∣ y$ と書きます。

整除関係において、約数を生成するよりも倍数を生成する方が簡単です。 $x ∣ y$ となる $(x, y)$ をたくさん生成したいとき、 $y$ ごとに生成するよりも、 $x$ ごとに $y = x, 2 x, 3 x, \dots$ を生成していくと効率的な場合があります。

特に、上限が小さい場合には、次が行えます。

上限 $X$ に対して、全てのペア ${(x, y) ∣ 1 ≦ x, y ≦ X かつ x ∣ y}$ を生成することを考える。このようなペアは $Θ (X \log X)$ 組存在し、その全列挙は $Θ (X \log X)$ 時間で行える。

$x$ ごとに $y$ を生成すれば、定数時間で $(x, y)$ が 1 組見つかります。 $(x, y)$ の個数は、 $\sum_{x = 1}^{A} ⌊ \frac{A}{x} ⌋$ で、これは $\int_{1}^{A} \frac{A}{x} d x = A \log A$ と十分近いです。二重ループで $Θ (A^{2})$ になるかと思いきや、むしろ $1$ 乗に近いオーダーになってしまう、初見だと間違えやすい計算量解析です。

解いていきます。 $A_{j} = x$ が見つかったときに、 $x$ の倍数が答から除外されると捉えます。ただし、自身が除外されてしまったり同じ値が複数回あるときの処理が厄介なので、私は、私は次の問題を考えました（公式解説は少し違う）。

各 $y$ に対して、 $A_{j} ∣ y$ となる $j$ の個数 $B (y)$ を数えよ。

$B (A_{i}) ≧ 2$ であるか否かによって、 $A_{i}$ が答に含まれるかが判定できます。

$F$ は、次のようにすればよいです。

$C (x) = （ A_{i} = x となる i の個数）$ とする。 $B (y) = \sum_{x ∣ y} C (x)$ である。
$x = 1, 2, 3, \dots$ 順に、 $B$ を表す配列の $x, 2 x, 3 x, \dots$ 番目に $C (x)$ を加算する。

上述のようにこの計算は $X = max A_{i}$ として $Θ (X \log X)$ 時間で行えます。 $C (x) = 0$ となる $x$ をスキップすると $Θ (X \log min {X, N})$ 時間にもできます。

ゼータ変換

$B (y) = \sum_{x ∣ y} A (x)$ として数列 $A$ から $B$ を得る操作は、ゼータ変換と呼ばれています。「ゼータ変換」は一般には隣接代数において定義され、整除関係のゼータ変換はその原型です。（競技プログラミングでは、（ $n$ 次元）累積和や集合の包含に関するゼータ変換の方が頻出です）。

ひとつの簡単な説明は、高次元累積和と結び付けるものです。例えば $10$ 以下の整数のうち、 $3$ -smoothな数（ $3$ 以下の素数のみを素因数に持つ数）を次のように並べてみます。

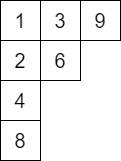
素数の方向を軸として、 $2$ 次元格子の一部ととらえています。ある自然数 $y$ の約数全体は、そのマス目から左上の長方形領域として表されます。約数に対する集計が、長方形領域に関する集計と同じことになり、各軸に対する累積和をとることで、ゼータ変換を行うことができます。（下の図では記号「 $+$ 」を省略しています）。

実装はおおよそ以下の通りです。 $X$ を計算する数列のインデックスの最大値とします。

for p in 2, 3, 5, 7, ...:
  for i in 1, 2, ..., X//p:
    B[p*i] += A[i]

この計算量解析はやや難しいですが、素数の分布に対する考察（素数の逆数和 $\sum_{p ≦ X} \frac{1}{p} = Θ (\log \log X)$ ）から、 $Θ (X \log \log X)$ であることが知られています。（提出例：■）

問題E – Smart Infants

最強園児になりたいです。

次の 2 つのデータを上手く管理します。

(A) 幼稚園ごとの、園児のレートの分布
(B) 全幼稚園に対する最高レートの分布

特に、「最大値や最小値をとる」「要素の追加や削除ができる」といったことができればよいです。転園に合わせて 2 つの幼稚園に対して (A) を変更し、最高レートを再計算。その計算結果に応じて (B) を変更してあげればよいです。

C++ の vector、Python の list などはこれらの操作を行うのに適していません。C++ の Multiset に相当するデータ構造、内部実装レベルでは、平衡二分木と呼ばれる木構造の類がこれらを扱うのに適しています。

Python でこれらを行いたい場合、競プロ環境下という制約がなければ、例えば http://www.grantjenks.com/docs/sortedcontainers/ などは妥当な選択肢のひとつです。

標準モジュールの範囲だと、https://docs.python.org/ja/3/library/heapq.html heapq を使うことで、「最小値」「要素の追加」が行えます。最大値は、順序を入れ替えた自作クラスに対して最小値を求める、あるいは挿入時に値を $- 1$ 倍してしまうことで扱えます。

要素の削除が問題です。例えば補助的に heapq や、数え上げのための defaultdict などをもうひとつ持つことで、「削除対象」を別に持って、最小値の参照の際にそれが実は削除済であるかを確認することで管理できます。ねぼこさんの記事も簡潔にまとまっています。またちょうど昨夜、Kiri さんによる Binary Trie を上手く利用した対処法も記事になっていました。私は、heapq と BIT だけで毎回適当な実装を考えてしまうことが多いですが、ライブラリ化しておくのもよいと思います。

今回の問題に関していえば、「園児の転園」「最強の幼稚園」など、データが園児や幼稚園と紐づいています。したがって、一度挿入しているデータが最新のものであるかどうかは園児や幼稚園の最新データを比較することで判定できます。

園児の最新の所属を管理する
幼稚園ごとに heap をもって、(レート, 園児) を入れておく（符号をつけて、最大レートが検出できるようにする）。
転園時には、転園元からの削除は行わず、転園先への追加のみ行う
最小値の検索は次のようにする
- 幼稚園データに保存されている最強の (レート, 園児) を見る
- 園児の最新の所属と一致していれば、それが最強園児
- そうでなければ、保存されている最強園児のデータを破棄して、ループ

これにより、常に幼稚園の最強園児が参照できるようになります。同じように、

(最大レート, 幼稚園) を全部入れた heap をもつ
最大レートが変更された場合には、追加のみ行う
幼稚園の最新の最強園児を検索することで、最小値が最新のものかを判断できる

といった要領で、各時点での「平等さ」を計算することができます。

問題F – Pond Skater

「 $K$ マス移動で到達できる範囲」を個々のマスから個別に生成すると間に合わいません。「 $K$ マス移動」を、「 $1$ マス移動」 $K$ 回に分解できるように捉えなおします。すると、

どのマス目を通っているか
何回目の移動であるか
その回の移動の何マス目であるか
どの方向に移動中か

などのデータに分解して問題を捉えなおすと良さそうです。最短移動回数が問われていることを考えると、各 (マス目, 方向) に対して、(移動回数、移動マス数) は最小のもの以外は捨ててしまってよいことが分かります。したがって、(マス目, 方向) をひとつの状態として、ダイクストラ法の要領で問題を解くことができます。私は方向として、「上下左右」に加えて移動の初手「次にどちらにでも進める」を加えた $5$ 通りを持ちましたが、利点が少なかったかもしれません。

なお、ダイクストラ法といっても、ほとんどの遷移がコスト $1$ なので、BFS に非常に近い部類になります。上手く実装することで、queue だけを使って計算量 $Θ (H W)$ を実現することができます。移動回数 $a$ 回目、の $b$ ステップ目を、 $(a, b)$ と書きます。

$(a, b)$ のうち、 $a$ が一定のものを、queue1 で管理する
$a$ が増える移動に備えて、もうひとつ queue2 を用意しておく
$(a, b)$ から $(a, b + 1)$ へ遷移するときは、queue1 に入れる
$(a, b)$ から $(a + 1, 0)$ へ遷移するときは、queue2 に入れる
同じ $a$ に対する処理がひと段落したタイミングで、queue1 と queue2 を入れ替える

私はダイクストラの方で実装してしまったのでソースコードはなしでｗ