| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
38分6完(4ペナルティ)で41位でした。
前回に引き続き、易しめなセット?少し出題方針に調整が入ってるかもしれないですね。
6問とも解き終えて、29分台で提出。順位表を見て「初の10位以内だ!」と思ったものの、Eで失敗していて残念。そのままボロボロとやらかして、結局過去最高順位とはほど遠い結果に。

Fがスムーズに超えられた!割と速くない?と思ったけれど、全体では2着でした。
というか手前に問題Cもこなしてて5分切ってるのすごいぞ!
問題C – C – Lower
各スタート地点に対する移動回数を計算したい。右から読んでいけばよい。
ゴール地点に対する移動回数を計算すると思うと、左からでも良いのですね。
pythonで速度を上げたい人は、numpyを使う方法があります。例えば私の過去記事
[numpy]連続同一値の数え上げ (AtCoder ABC-129 D)
を参考にしてください。また、今回の問題に合わせて書くと、例えば次のような解答になります。
https://atcoder.jp/contests/abc139/submissions/7281481 (175ms)
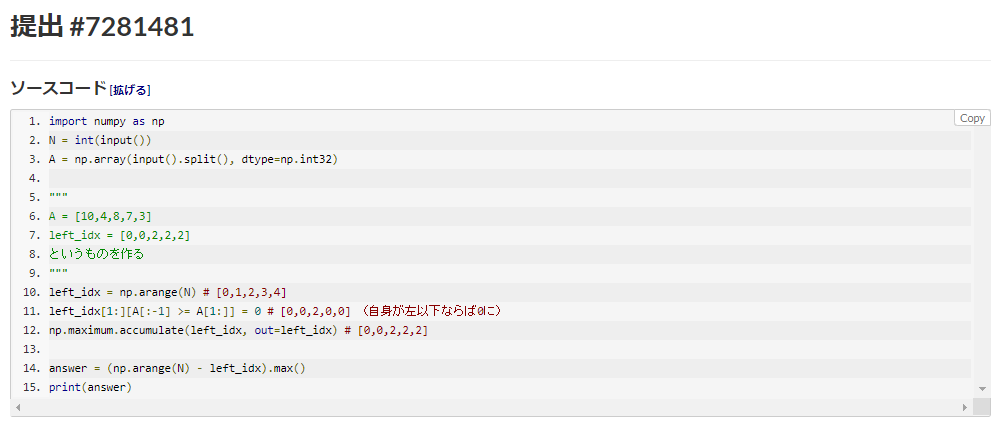
numpyのimportと入力の受け取り・array化に実行時間の大半を割いていて、計算自体は高速になっているので大規模データだとforループより有利になります。
https://atcoder.jp/contests/abc139/submissions/7281481 → 175ms
https://atcoder.jp/contests/abc139/submissions/7281668 → 178ms
んw 計測難しい。
問題D – ModSum
サンプルが親切すぎて、「13 → 78」の時点で、計算好きな人は予想が立っちゃいますよねw
N=1まわりを確認しても、特に不規則は現れない(これもサンプルにある)し、かなりの易問。
証明なき提出をした方も多いかもしれません。
・実例:P = [2,3,4,5,1] などとする。このとき 1+2+3+4+0を実現できる。
・証明:P[i] = xのとき、M[i] <= x-1 になるのでこれ以上は無理。
問題E – League
各段階で「現時点で行える全ての試合を行う」が最適。要するに
・人 $n$ の第一希望を 人$m$ とする。人 $m$ の第一希望も 人$n$ なら、この対戦を処理。
証明は帰納的に「最適解の先進性」を示す形で行えます。
ボーっと $O(N^2)$ だと思ってしまいましたが、日数が $O(N^2)$ かかるパターンがあって、最悪計算量は $O(N^3)$ となります。雑実装で良いと思っていたらPythonでもPyPyでもTLEを食らいました。PyPyで1件TLEしたのが意外…PyPyは何がどう速くなるのか理解できていないので、私は上手く小手先の定数倍改善ができません。
とりあえず本質的に計算量が縮むので。最悪計算量のとき、前日と状況が変わっていないところを何回も見るのが悪いのでそこを改善します。このアルゴリズムに沿ったとき、
・$n+1$ 日目に試合をする人は、どちらかは $n$ 日目に試合をしている。
という性質があります。こうすると、1回の探索は前日または当日の試合に絡むので、探索回数が $O(\text{総試合数})$ で抑えられて、$O(N^2)$ 計算量になります。
(後日談)制約を $N\leqq 100$ と勘違いしていました。この程度の $N^3$ が通らないのは意外だなぁと思っていましたが、当然だった。
問題F – Engines
よって安易な貪欲は難しく、「何かを決め打てば貪欲できる」を考えます。
雑に、ある一方向の集中させたい気持ちになります。目的の一方向が決まれば、貪欲っぽいことができそうです。
・x軸正方向はすべて取っているはず
・x軸負方向はすべて取っていないはず
・半平面 $S_+$ 内のベクトルは全部とる
・半平面 $S_-$ 内のベクトルは全部とらない
という戦略が解の必要条件として挙げられます。
$N$ 個の点を半平面で区切る方法は、約 $N$ 個しかありません。原点から見た角度でソートして点を持てばよく、区切り方は尺取りで1件あたり平均 $O(1)$ で求められます。累積和を用意すれば、1件1件の解の候補は $O(1)$ で計算できるので、解は $O(N\log N)$ で計算できます(ソート)。問題 F でこんなに計算量に余裕があるのはめずらしい。
・「半平面をとる」 → 「ある連番でとる」
と候補を広げて全部計算しました。これで $O(N^2)$ 解法です。

