| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
19分+1ペナで23位。易しい回でした。
Fが5分で提出できて、結構速いと思いきや、FAは3分なんですよね。
問題B – Multiplication 2
TLE する愚直解:

左から順にかけていくと、最終的に $1800000$ 桁程度の数の計算になります。多くの言語では整数型のオーバーフローを引き起こし、Pythonの多倍長整数では正確に計算できるものの、やはり桁数が大きいことで演算 $1$ 回あたりの計算コストが大きくなって、TLEです。
愚直解の高速化(AC):

a, b, c, d の積を計算するときに、a, ab, abc, abcd と順に計算するのではなく、「[a,b,c,d] → [ac,bd] → [abcd]」と計算しています。とても大きな整数の演算回数が抑えられて、ACになりました。
※ もちろん、$10^{18}$ を超えたら正確な計算はやめるのが良い解法かと思います。
問題C – Multiplication 3
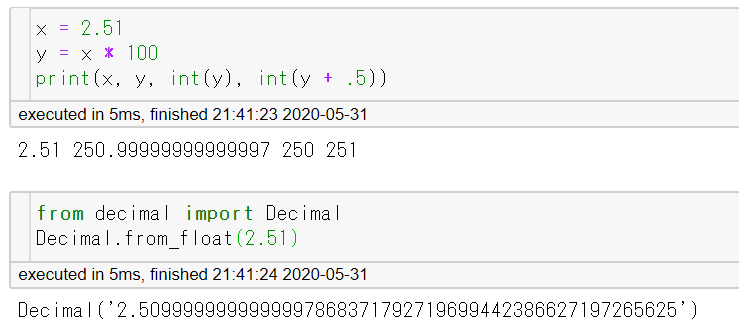
計算誤差に関する出題です。Pythonでは、小数型は、通常 2 進法表示 53bit分の有効数字しか持たず、それより下の位は切り捨てられてしまいます。10 進法での有限小数であっても 2 進法では一般には無限小数になるので、その正確な値を保持できないことが分かります。例えば上の例では、$x = 2.51$ と print されていても、内部的には
2.5099999999999997868371792719699442386627197265625
を正確な値として扱っていることが分かります。(Pythonに限定された話ではなく、一般的な言語における小数の扱いは多かれ少なかれこのような形式です)。
この小数の挙動はしばしば計算誤差を引き起こします。とはいえ、計算結果が $2^{-53}$ 倍ずれてしまう(不正確な表現)程度のものなので、多くの場合には無視量なのですが、本問題ではほんの少しの誤差が致命的になってしまいます。例えば積 $AB$ の計算結果が $100.01$ と $99.99$ では、出力すべき値が変わってしまいます。$2^{-53}$ の規模の誤差も許容できない出題ですので、整数型などを上手く使って計算する必要があります。
- 高い桁数の精度を持つ Decimal クラスをうまく使う
- 小数点より左側,右側を文字列として検出することで、$100B$ の正確な値を整数でとる
- $100B + 0.1$ を切り捨てるなどして、誤差に影響されずに $100B$ の整数部分を抽出する
などの方法があります。
(以下個人的なこと:$2.5099999999999997\cdots$ を $2.51$ と判断して print してくれるってのの記憶と混同して、int(100*B) で良かったような…と勘違いして 1 ペナ。恥ずかしい。)
問題E – Count Median
これ面白い問題ですね。びっくりしましたw
中央値が一番小さいのは、全部 $A_i$ とした場合、一番大きいのは全部 $B_i$ とした場合です。そして、それらの場合の中央値の間を「全部」とる($N$ が奇数なら $1$ 刻み、偶数なら $0.5$ 刻み)というのが本問の結論です。
ABCでも複数回(考察の一部として)見かけた、次の類例をもとに着想しました:
- $A_i\leq X_i\leq B_i$(全部整数) のとき、$\sum X_i$ は何通りの値をとるか?
これは当然、$\sum A_i$ と $\sum B_i$ の間の連番を全部とるというものです。最小値の状態から、和を $1$ ずつ増やしながら最大値の状態にうつせることが根拠です。
たとえば、$N=3$, $(A_i,B_i) = (0,2)$ (すべての$i$)であれば、
$$(0,0,0) \to (0,0,1)\to (0,0,2)\to (0,1,2)\to (0,2,2)\to (1,2,2)\to (2,2,2)$$
とするという要領です。この過程で総和は、最小値から最大値まで連続的に推移しますから、連番を全てとってくれます。
中央値でも同じことが言えました。同じように最小値と最大値の間を動かしてあげると、中央 $1~2$個の和は連続的に推移します。
問題F – Knapsack for All Subsets
わずか2ヶ月前に、似た例題があったので、その経験が活きた方も多いのではないでしょうか?
過去問の経験がなくても、今回の問題の方が簡単な気もします。例えば、サンプル 1 :$A = [2,2,4]$ を解きましょう。
$f_1 = 1 + x^2$, $f_2 = 1 + x^2$, $f_3 = 1 + x^4$ とします。各部分集合 $T$ に対する答は次のようになります。
- $T = \{1,2,3\}$ に対する答は、$[x^S] f_1f_2f_3$ です。
- $T = \{1,2\}$ に対する答は、$[x^S] f_1f_2$ です。
といった要領ですね。結局、次の計算結果の $x^S$ の係数をとればよいです。
$$ f_1f_2f_3 + f_1f_2 + f_1f_3 + f_2f_3 + f_1 + f_2 + f_3. $$
$S\geq 1$ なので、 $1$ を足してしまって、$(1 + f_1)(1+f_2)(1+f_3)$ の計算をすればよくて、結局 $[x^S] \prod_{a\in A} (2 + x^a)$ を計算するだけの問題になりました。
「$1$ を足して因数分解する」が見えなかった場合は、適当な場合分け軸で計算対象を分割すると思いましょう。例えば $f_3$ が入っているかどうかで分けると
$A = f_1f_2f_3 + f_1f_3 + f_2f_3 + f_3$, $B = f_1f_2 + f_1 + f_2$ などと書いてみる(計算対象は $A+B$)と、$A = (1+B)f_3$ のような表示が見つかり、これを一般の $n$ でやってあげれば同じように解くことができます(結局ほとんど同じ計算になります)。

