| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
59 分 6 完 + 5ペナです。447位でした。
Fでペナ出し過ぎたのはひどいですね。2ペナ分は戦略的なデバッグ用提出なのですが。あとは、手元でシミュレーションのコードをさっさと自作してテストした方が良かったです。
こういう F はあんまり解かれないやつで、適当に全完すればそこそこの順位になると思い、適当に提出しちゃった感。甘かったですね。自分が rated の回にこういうおかしな立ち回りをしないように気を付けたいと思います。
今週も問題Cの最難クラスか?というように見えました。連結成分ごとに最大値…最大値でもダメで、 $2$ 位までを集計する感じかな?できるけど少しだるいやつだなーと。道、一本でしたね。こういうのがギャグというジャンルでしょうか?
hate を含む問題名が
問題D – I hate Factorization
問題名はヒントのつもりなのでしょうか?素因数分解や約数列挙に基づかなくともできるよという。
解法は例えば次の 2 つがありそうです。
(1)$A-B$ は $X$ の約数である。ここから $A-B$ の候補を列挙する。$A-B=d$ と固定すると、方程式 $(B+d)^5 – B^5 = X$ は $B$ に関する $4$ 次方程式。$f(x) = (x+d)^5 – x^5$ は、$x\geqq -\frac{d}{2}$で単調増加なので、実数解が二分探索で求まる。そこが整数解になっていれば答。
(2)そもそも $5$ 乗数は、十分疎です。例えば $|x| > 200 \implies (x+1)^5 – x^5 > 10^9$ が確かめられます。$f(x) = x^5$ は(負の数を含めても)単調増加なので、隣との差が $10^9$ を超え始める部分から先は、隣じゃない選び方も含めて使いようがありません。
よって $|A|, |B| < 200$ くらいを探索するだけで解けて、制限時間内に余裕で全探索可能です。
(余談)経験上、競プロの問題のほとんどが、64bit整数の範囲で計算ができるように設計されています。$|A^5| < 2^{63}$ くらいで解ける設計なんだろうなあと思うという方法で、「実は小さい範囲だけ調べれば良いかも」という発想が得られるかも。
問題 E – This Message Will Self-Destruct in 5s
ABC-E では最易問クラスでしょうか?そもそも易しいですし、同様の考え方を使う問題は最近のABCコンテストでもよく見ます。
単純に全ペア $(i,j)$ を見ようとすると計算量が $\Theta(N^2)$ になるので、何らかの基準でまとめて集計する必要があります。流石に、 「$i$ が一定のところ」 「$j$ が一定のところ」などをまとめて計算するのは真っ先に浮かべるべき選択肢でしょう。
絶対値が扱いにくそうですが、順序を入れれば解決です。$i < j$ とすると、条件は $j – i = A_i + A_j$ と絶対値のない形で表せます。 $j$ ごとにまとめようと思うと、$A_i + i = j – A_j$ と変数分離するのは難しくなくて、あとは各 $x$ に対して $A_i + i = x$ となる $i$ の個数を持ちながら計算していくことができます。
python なら、 collections.defaultdict を使うのが簡単です。dict 型と大体同じですが、キーが存在しない場合にデフォルト値を返してくれます(参照しただけでキーが登録されてメモリを圧迫するなど、dict と比べた副作用も存在しますが、競プロでは影響が少ないです)。
問題 F – Three Variables Game
まず不変量として、$A+B+C$ が一定だなあと思います。パラメータ $(A,B,C)$ は実質 $2$ 次元を動くことが分かります。

幾何学的には三角形の重心座標のようなものです。三角形 $ABC$ を含む平面上の点 $P$ の位置ベクトルは、$\vect{OP} = s\vect{OA} + t\vect{OB} + u\vect{OC} (s+t+u=1)$ の形に一意に表せ、三角形の内部という条件が $s,t,u > 0$ に対応したりします。上の図だと、$(s,t,u)$ の代わりに $(3s,3t,3u)$ を座標とした格好です。
各時点での要求は、3つの座標軸方向について $\pm 1$ のどちらか移動せよというものです。
とりあえず、1手読みで死なないように努力しようとすると、なるべく正三角形の内側に移動したい気持ちになります。
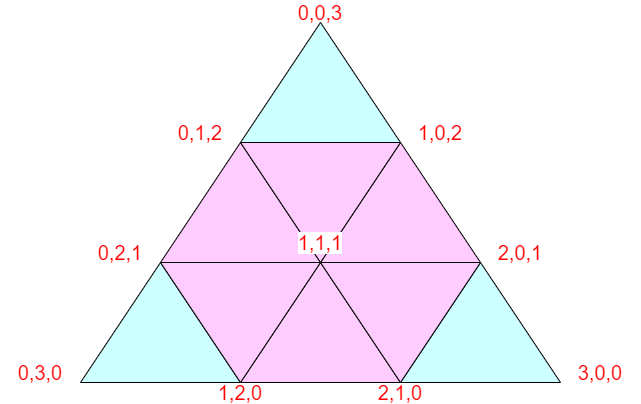
上の六角形に居るときに、どの軸を要求されても六角形の中に留まれることが分かります。$N\geqq 3$ かつ $(A,B,C)$ が $3$ 頂点でないときは、この方法でずっと生存できることが分かりました。
初手に $3$ 頂点に居るときだけが問題です。まぁこれは、初手で死亡確定 or 安全圏に入るので OK です。
よってあとは、$N$ が $1$ または $2$ のときだけが問題です。$N=1$ のときは、常に選択肢が $1$ 通り以下なので簡単です。
$N = 2$ とします。やっぱり内側にとどまりたい気持ちで考えます。
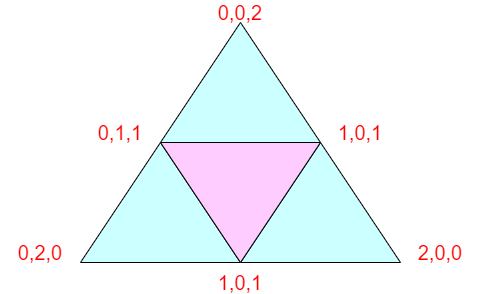
$N=2$ のときは、$3$ つの中点および $3$ つの頂点からなります。移動方向によっては中点からはみ出ざるを得ません。しかし、はみ出る方向が $2$ 種あります。これらを使い分けると、 $2$ 手先にまた中点に戻ってこられることが分かります。
よってこの場合も、初手で死亡確定している場合以外は生存です。中点に移動できるなら移動して、そうでないときは $2$ 手読みで $2$ 手後に中点に戻れるようにします。
地味に、同じロジックを何度も実装しない工夫が大変でした。というか、私もわりと設計が甘いかもしれません。

