| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | |
| 結果 | AC | AC | AC | AC | AC |
全体感想
24分5完で、109位でした。
万全のフル参加で解けない問題があったのは、ABCでは久しぶりです。ABC 最難か?と思ったのですが、個人差かもしれません。振り返ると、個人的 2 強が「path pass i」「Colorful Tree」でジャンルもろ被りですから、この辺が苦手だと明確に意識させられます。
コンテストで解けない問題が出て、しかも unrated なのは、勉強になってオトクです。
問題D – Sum of Large Numbers
選ぶ個数を固定すると、作れる数としては、最小に作った場合と最大に作った場合の間の連番すべてになります。例えば このような方法 で確かめられます。よって、連番の和集合を数え上げる問題になります。
さらに、これらの連番が重複しないことがわかります。$10^{100}$ がとても大きいということがここで使われます。想像しにくい人は、例えば $10000, 10001, 10002, 10003$ の部分和を書き並べてみましょう。計算結果はほぼ最上位だけから概算されて、計算結果を見れば足した個数が復元できます。
よって和集合を数え上げるといっても、各々の個数に対する計算を足すだけです。最大・最小値は、「累積和の要領で計算する / 等差数列の和として計算する」などの方法があります。$101$ 桁の整数は $2\cdot 10^5$ 個足しても $106$ 桁におさまるので多倍長整数を使ってもよいですし、$10^{100}$ を無視して端数部分だけ計算する方が簡単です。
また、答は $N, K$ の 多項式次式になります。「高校数学典型の要領で和の計算をする」「小さな $N, K$ の場合を愚直計算して多項式補間する」などの方法をとれば、$\Theta(1)$ 時間で答を求めることも可能です(私はやっていません)。
問題E – Active Infants
活発度が大きい子をなるべく遠くに移したいという気持ちになります。これは単純には誤りなのですが、貪欲法の正当性の検証に慣れていれば、次が発見できると思います:
・活発度が最大の子は、右端または左端に移すとしてよい。
各時点での状態に容易に優劣を定められることもありますが、複雑な場合は、2つ入れ替えを観察するなどして、最適解の構造を探るのが基本です。今回は、活発度最大のうちひとりを $i$ として、最適解において次が成り立ちます。
(1)$i$ が左(元の位置も含む)に移動している場合:移動先が左端でないとする。人 $j$ が左端に移動しているとして、$i$ と $j$ の移動先を交換すると、うれしさが非減少($i$ の移動距離の増加 $\geqq$ $j$ の移動距離の減少となることから)。特に、最適解のうちで、人 $i$ が左端に移動するものが存在する。
(2)$i$ が右に移動している場合:同様。
として、「人 $i$ が左端または右端に移動するような最適解が存在する」ことが証明できます。
このような考察だけで 1 つの最適解を構成できてしまうこともありますが、今回は各時点で 2 択に絞り込まれるにとどまりました。しかしこれだけでも探索空間が著しく狭められていて、十分な成果です。
最適解を探すにあたって、まだ並べていない人は端のどちらかに並べるとして、活発な子から処理していきましょう。1 人あたり 2 通りの並べ方しか考慮する必要がなくなり、途中経過は「両端から何人かずつ」という $\Theta(N^2)$ 通りなので、計算量 $\Theta(N^2)$ の dp で解くことができます。
dp = np.zeros(1, np.int64)
for n, (i, x) in enumerate(zip(I, A)):
newdp = np.zeros(len(dp) + 1, np.int64)
left_ind = np.arange(len(dp))
right_ind = N - 1 - n + left_ind
left_cost = x * np.abs(left_ind - i)
right_cost = x * np.abs(right_ind - i)
np.maximum(newdp[:-1], dp + right_cost, out=newdp[:-1])
np.maximum(newdp[1:], dp + left_cost, out=newdp[1:])
dp = newdp(並べた人数、左に並べた人数) をキーとして dp の計算をします。
ひとつずつ時系列を進めていくような dp では、最新の値しか持つ必要がないです。空間計算量を節約する(慣れた人向けの?)テクニックとして語られることが多いですが、個人的に 2 次元ではなく 1 次元の配列を相手にすればよくて思考が楽なので、私はむしろ初期からそういう実装をしています。
問題F – path pass i
はじめ、かなりややこしい方法で解いてしまいました。2 時間以上かかりましたが、自力 AC はできました。
提出:https://atcoder.jp/contests/abc163/submissions/12151858
関連ツイート:
これを説明しても良いのですけど、割と大変解法なのですよね。単純パスを LCA ごとにまとめて数え上げます。でも各頂点 $v$ に対して、全ての色の単純パスを数えていてはダメです。代わりに「あとで $n$ 回足すことにしましょうね~」という $n$ を持ってインクリメントしていきます。「この頂点を根とした場合に色ごとにいくつパスを持っていますか?」という値を持って下から木 dp していき、 Weighted Union Heuristics (「マージテク」と呼ばれがち)(要素数の合計 $N$ のデータ構造たちをマージするとき、要素数の小さい方から大きい方へ 1 要素ずつ移せば、要素の移動回数の合計が $\Theta(N\log N)$ になるというもの)を用いると、$\Theta(N\log N)$ で解けます。ただでさえ、値の計算を保留しながら遅延計算に必要な情報を持つのがややこしいのに、移す側・移される側で計算式も違ってきて、正確な立式にかなり苦労しました。
さて、まとも解法の方も説明しておきます。
なんと、木グラフの単純パスの個数は、頂点数のみから定まります。あー、これがすべて…。「木グラフ 単純パス 数え上げ」などでぐぐったりしたのですが、コンテスト中にここに至ることはなかった。(しかし、$2$ 点を決めるパスがちょうど $1$ つあるというだけの話なので、明らか)。
このことに気づくと、各色 $k$ の補集合ごとに、頂点数が取得できればよいことが分かります。ここまでくれば、木dp + Weighted Union Heuristics による $\Theta(N\log N)$ 解法は分かりやすいと思います( https://atcoder.jp/contests/abc163/submissions/12159656 )
def merge(A, B):
if len(A) < len(B):
A, B = B, A
for key, cnt in B.items():
A[key] += cnt
return Aさて、各頂点において大きなデータ構造を参照したい場合、ひとつのデータ構造だけを持ちながら木グラフを探索するのも典型手法です。DFS による木グラフ探索は Euler Tour とも呼ばれます。(この問題をよりちゃんと理解するため、という目的だけではなかったのですが)ちょうど、Euler Tour について自習しましたので、よければそちらも参考にしてください。
今回取り扱う連結成分は、部分木から部分木を引いたものです。Euler Tour では部分木が区間になるので、部分木たちを対象とする計算に適しています。
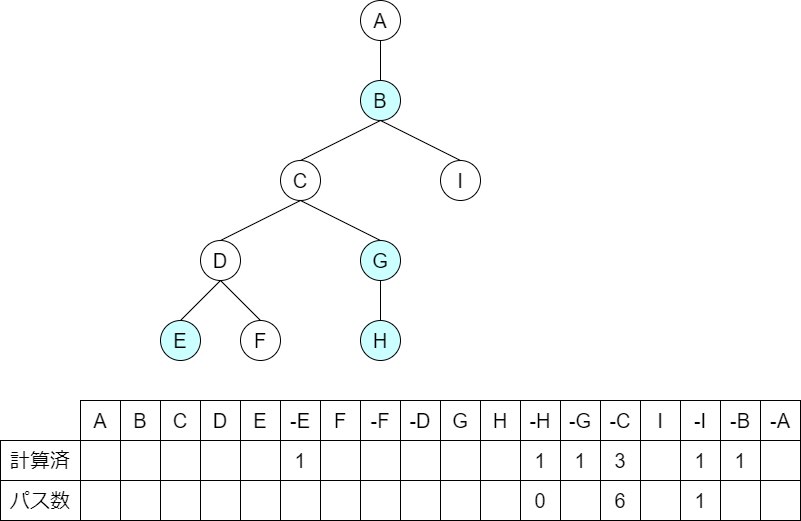
色が $1$ 色しかないとして、考えていきます。頂点に $A$ から $I$ までのラベルがついた木グラフのEuler Tour を書きました。頂点数 $x$ がわかれば、色を含まない単純パスの数が $x(x+1)/2$ 個できるので、目的は、連結成分ごとに、頂点数を求めることです。
(頂点 / 辺 / 連結成分)といった色々なものに対する計算を木グラフについて行うとき、計算対象をひとつの頂点に紐づけて考えるのがよくある考え方です。例えば辺は葉側の頂点と対応させて見ることが多いです(根側だと、頂点に対してたくさんの辺があるので対応が分かりにくい)。
今回は連結成分を計算するのですが、それぞれの LCA に紐づけて計算しましょう。つまり、上図では $2$ つの連結成分 $\{A\}$, $\{C,D,F\}$, $\{I\}$ がありますが、それぞれの計算を頂点 $A, C, I$ が受け持つと考えます。頂点 $A$ (根)に紐づく連結成分の他に、それぞれの色点を親に持つ頂点が計算対象となります(ついでに $H$ のところで大きさ $0$ の成分があると思うと統一的に見やすいです)。
例えば、頂点 $C$ においてはどのような計算をすべきでしょうか?まず、部分木の大きさは Euler Tour から簡単にとれます。そこから、葉側にある「色点」「同色の部分木」の頂点数を全部引くことで、$C$ が受け持つ連結成分の大きさを計算することができます。
計算過程も上の図に含めました。連結成分 $\{C,D,F\}$ は、$C$ を出る瞬間($-C$)に行います。Euler Tour 順に計算を進めていれば、 $-C$ の時点で部分木の計算は既に済んでいます。
部分木の大きさが $6$ (Euler Tourで 区間 $[C, -C)$ に対応)です。区間 $[C, -C)$ において計算済の頂点数(この場合 $1, 1, 1$ で $3$ つ)を求めることで、連結成分の大きさが $x = 6 – 3 = 3$ であることが分かります。パス数 $6$ を計算しつつ、$3$ つの頂点を計算済として表を更新します。$A$ を含む成分については、区間 $[A, -A)$ で計算済となっている頂点数を $N$ から引けば求まります。
あとはこれを高速化します。たびたび「区間における計算済頂点数の和」が必要になります。区間和といえば累積和なので、実際には累積和の形で持ちましょう。

あとはこれを、全ての色について同時にやります。こういう表を持とうとすると、$\Theta(N^2)$ の大きさのデータになってしまい上手くいきませんが、計算を $1$ ステップ進めるときに更新される色は $2$ 色以下ですので、計算を進めながら配列を in place に更新していきます(色ごとに座圧するのでもよいですが、実装がだるそう)。頂点 $C$ においては、$[C,-C)$ での累積和が必要でしたが、時刻 $C$ の時点での必要な色の値だけメモしておけば、あとで必要な減算を行うことができます。
提出例: https://atcoder.jp/contests/abc163/submissions/12191972
ちょいちょい高速化: https://atcoder.jp/contests/abc163/submissions/12198896
言語アプデ適用されましたが、アプデ適用がない前提で実装してしまう癖があります。過去問環境に適用されてから、練習を積みます。

