| A | B | C | D | E | F | |
| 問題文 | ■ | ■ | ■ | ■ | ■ | ■ |
| 自分の提出 | ■ | ■ | ■ | ■ | ■ | ■ |
| 結果 | AC | AC | AC | AC | AC | AC |
全体感想
37分6完1ペナルティで22位でした。
37分は、過去のABC(6問)での自己べタイムみたいです。1ペナがもったいなかったけど、上出来ですね♪
はじめにEを7:30で提出したのですが、ここでバグを出していました。FA狙えたっぽかったな、惜しい(提出結果を見守らず問題Aに進んだのもFA逃しの要因)。
問題Cを誤読していて死にそうになりました。
問題A – Can’t Wait for Holiday
weekday = 'SUN,MON,TUE,WED,THU,FRI,SAT'.split(',')
dic = {x:7 - i%7 for i,x in enumerate(weekday)}{‘SUN’: 7, ‘MON’: 6, …}
としても良いですが、こんな感じで書いてみました。
問題C – Buy an Integer
しばらく、$d(N)$ を、「$N$ の各桁の和」と勘違いしていました(これでも解けますが、Eくらいありそう)。昨日、誤読で反省したばかりだというのに…。
・桁数を固定して考える
・値段に単調性があるので2分探索
などの方法があると思います。後者で解きました。自然数 $N$ の桁数は、
len(str(N))でOKです。
問題D – Coloring Edges on Tree
グラフの辺彩色といえば、知識としては
・[Vizing の定理] 辺彩色数は、$\Delta(G)$ または $\Delta(G) + 1$ に等しい
・[Konig の定理] 2部グラフの辺彩色数は、$\Delta(G)$ に等しい
などを一応装備しています。木グラフは2部グラフなので、辺彩色数は $\Delta(G)$ に等しい、と思考しました。いや、流石に木グラフなので、もっと簡単事情ですがw
今回は、適当に上から塗っておけばよいです。
(1) 色情報の持たせ方
今回のように、木グラフの辺に関する情報を扱う場合、「頂点を見ている」のか「辺を見ている」のかで思考が乱れやすいです(主観)。なるべく概念の定義を厳密にすること、なるべく頂点に関連付けることなどを意識します。根付き木と見たとき、根以外の頂点は、唯一の親を持ちます。このことから、
・$v$ の親が $p$ であるとき → color[v] に辺 $pv$ の色を持たせる
と定めて色を管理しました。
(2) 再帰を避ける (Pythonを中心に)
グラフのdfsは、入力次第で再帰回数がかなり深くなり、適当な回数を超えるとエラーになります。深い再帰を扱う方法として、
import sys
sys.setrecursionlimit(10 ** 7)というような対策方法が1つ存在します。ただこれも常に宣言通りの再帰上限で挙動するわけではなく、環境次第で上手く動作しなくても文句は言えません。
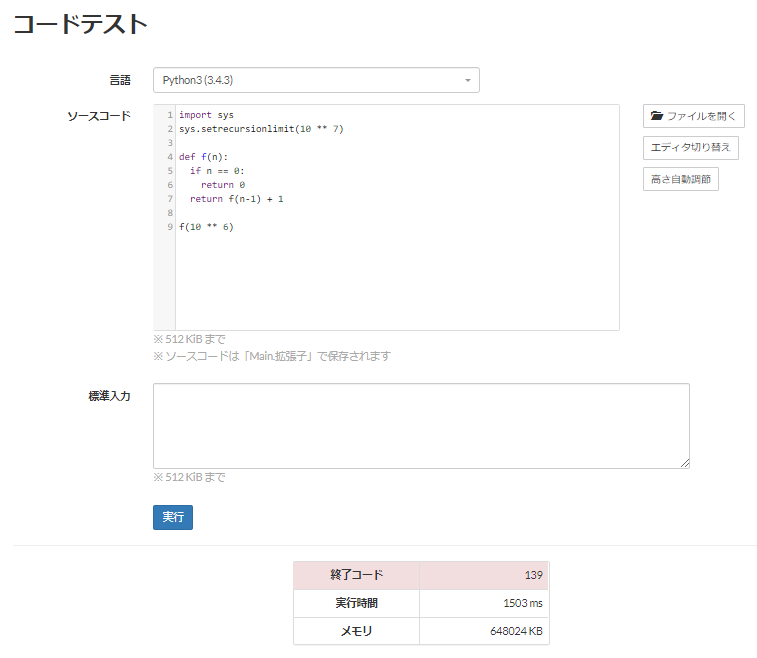
もうちょっと頑張って再帰上限回数をいじる方法も存在しますが、事情は大きく変わりません。
詳しい説明は省きます(ちゃんと書けるほどの理解がないので)が、基本的には関数の深い再帰は負荷も大きく、パフォーマンスが悪くなりやすいです。(そもそも、デフォルトの再帰上限回数が小さく設定されている理由を想像してみましょう。単なる嫌がらせ?流石に違うはずで。)
私は最近では、sys.setrecursionlimit は全く使わない方向にシフトしています。木グラフであれこれする場合は、
・親から子側へ向かう、topological 順序を計算する(リストをstackとして使う)。
・for ループの形で、親側・あるいは子側から処理していく。
という手順を踏みます(同時にやることもできるけど、処理を切り分けた方が頭を使う量を減らせると思います)。
今回の問題の実装例:■
他には例えば:EDPC V – Subtree
現状、これをやっただけでも、Python (or PyPy) での実行速度最速になる割合がかなり高く、関数の深い再帰を避けている Python 競プロ勢はほとんど居ないと思われます。ぜひお試しください。
※ 深い再帰でエラーが出たり、パフォーマンスが下がるのは、Pythonに特化した話ではないです。

